Euler's formula for e^x

We want to prove the identity \begin{equation}\label{eq:euler_e} e^x = \lim_{n\rightarrow\infty} \left( 1+\frac{x}{n}\right)^n. \end{equation} If we consider the Taylor series for $e^x$, on the left hand side we have \[ e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots \] On the right, we can expand out the product using the Binomial Theorem \[ \left( 1+\frac{x}{n}\right)^n = \sum_{i=0}^n \frac{n(n-1)\cdots(n-i+1)}{i!}\left(\frac{x}{n}\right)^i = \sum_{i=0}^n \frac{x^i}{i!} \frac{n(n-1)\cdots(n-i+1)}{n^i}.\] The coefficient of $x^i$ equals \[ \frac{1}{i!} \frac{n(n-1)\cdots(n-i+1)}{n^i} = \frac{1}{i!} \frac{n}{n}\frac{n-1}{n} \cdots \frac{n-i+1}{n}.\] As $n\rightarrow \infty$ each term here containing $n$ converges to $1$ giving \[ \lim_{n\rightarrow\infty} \left( 1+\frac{x}{n}\right)^n = \sum_{i=0}^\infty \frac{x^i}{i!},\] or exactly the Taylor series for $e^x$.

You might think this argument has made somewhat cavalier use of limits. The following argument, adapted from [1, pg 272], is close to Euler's original. He was even more bold in his use of limits!

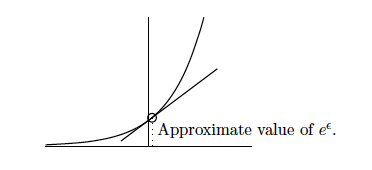
Thinking about $e^x$ near $x=0$, and its gradient, we see that, for infinitely small $\epsilon$ \[ e^\epsilon = 1 + \epsilon \] This is illustrated above. Let $x$ be any given number, then $N=x/\epsilon$ is infinitely large. So %\begin{eqnarray*} %e^x = e^{N\epsilon} & = & (e^\epsilon)^N \\ %& = & (1+\epsilon)^N \\ %& = & \left( 1 +\frac{x}{N} \right)^N. %\end{eqnarray*} \[ e^x = e^{N\epsilon} = (e^\epsilon)^N = (1+\epsilon)^N = \left( 1 +\frac{x}{N} \right)^N. \] Written in terms of limits, the infinitely large $N$ would give us (1).

Reference

[1] C.H. Edwards, The Historical Development of the Calculus, Springer-Verlag, 1979.