Hailstones revisited

"Mathematics is not yet ready for such problems." This is what the mathematician John Conway reportedly said about the Collatz conjecture, a simple-looking, yet unsolved mathematical mystery. This week Plus hosted two intrepid work experience students, Sabrina Qian and Joe Dickens, who decided to have a go at this fiendish problem nevertheless. And they made some intriguing discoveries. Here is what they came up with.

What are hailstone sequences and what's the Collatz conjecture?

Starting with any positive integer n, form a sequence in the following way:

• If n is even, divide by 2 to get a new number n'= n/2
• If n is odd, multiply by 3 and add 1 to get a new number n'=3n+1
.

Now take n' as your new starting number and repeat the process. For example,

n=10 gives the sequence

5, 16, 8, 4, 2, 1, ...

and n=25 gives the sequence

76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, ...

A sequence formed in this way is known as a hailstone sequence because the values bounce up and down just like a hailstone in a cloud.

When you experiment with different values for n you will soon find that every hailstone sequence appears to end up with the cycle 4, 2, 1, 4, 2, 1... and so on. Below we've plotted a few sequences starting with different numbers.

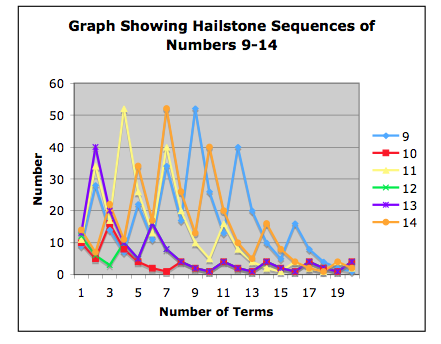
But can it be proved that every starting value will generate a sequence that ends up with the cycle 4, 2, 1? This is the unsolved problem known as the Collatz conjecture — no-one has so far been able to prove it.

What can we prove?

There are, however, some things we can prove. First of all, we can prove that 4, 2, 1 is the only simple recurring pattern. A simple recurring pattern is one that only involves one odd number, so that the transformation 3n+1 is only used once. In the example 4, 2, 1 the only odd number is 1 and the only time 3n+1 is needed is to transform 1 into 4.

Suppose a simple recurring pattern contains the odd number n. Then 3n+1 must be a multiple of 2n. This is because you must be able to return to the number n starting from 3n+1 using only division by 2. In other words, we have:

3n+1 = y2n,

where y is some positive integer.

Since y is a positive integer, the smallest it can be is 1. If y=1, then

3n+1= 2n. This clearly cannot be true, because n is a positive integer, meaning that multiplying it by 3 will give a larger answer than multiplying it by 2. If we take the next lowest value of y, which is 2, we get the equation:

3n+1=4n.

Solving this for n gives

n=1.

This gives us the repeating pattern 1,4,2,1,4,2,... .

If we increase the value of y, so that y is at least 3, we get

3n+1 = y2n ≥ 6n, which means that

1 ≥3n,

so

1/3 ≥ n. This clearly cannot be true if n is a positive integer. Thus we have proved that 4, 2, 1 is the only simple recurring pattern. If a hailstone sequence eventually settles on a simple recurring pattern, then this pattern has to be 4, 2, 1,... . However, this does not prove that there aren't recurring patterns involving more than one odd number.

Another thing that can be proved is that there are infinitely many numbers which, when "hailstoned", will produce the recurring pattern 4, 2, 1. In fact, any number n of the form

n=2^m, where m is a positive integer, will generate a hailstone sequence which eventually settles on the 4, 2, 1 cycle. Clearly such a number n is even, so the first step in the hailstoning process is a division by 2 to get 2^m-1. If m-1=0, then 2^m-1=1, so we have reached our 4,2,1 cycle. If m-1 > 0, then 2^m-1 is even, so the next step in the hailstoning process is also a division by 2. Repeating this argument shows that all the numbers in the sequence are even, so all the steps in the process are divisions by 2, so we eventually get down to 4, then 2, then 1. This is true for any positive integer m, which proves that there are infinitely many numbers which when hailstoned eventually settle on our cycle. However, this doesn't prove that every number, when hailstoned, produces a sequence settling on 4, 2, 1. If this seems strange, here's a simple analogy: there are infinitely many even numbers, but that doesn't mean that every number is even.

Curiosities

When trying to start working on the problem, we looked into many areas of it, hoping to find some clues to help us when we tried to work out other things. One of the first areas we looked at was how many terms of hailstoning it took for the sequence to reach its first 4. At first the number of terms seemed fairly random, when starting with 5 it took 3 terms, when starting with 6 it took 6 terms, when starting with 7 it took 14 terms and when starting with 8 it took only one term. However, after some time it became apparent that there were some curious links between numbers.

The first thing that we noticed was that after a while some doubles began to appear. Doubles was the term we used when two consecutive numbers took the same number of terms to produce their first 4. The first example of this was when we hailstoned 12 and 13, which both took 7 terms to reach their first 4. This was followed by 14 and 15, which both took 15 terms to reach their first four. Although the distribution of the doubles seemed random, they consistently appeared, and before long there were also triples, quadruples and even quintuples! Below is a list of all of the doubles, triples, quadruples and quintuples that we found when hailstoning the numbers 1 to 184.

Another curiosity is that all of the doubles consist of an even number followed by an odd number (rather than the other way around), and that most of the doubles seem to come in small groups. It also seems strange that there are more quintuples than quadruples — surely it seems more likely to have 4 in a row than to have 5 in a row? And finally, why are there so many doubles, triples, quadruples and quintuples? If they appeared occasionally, they could be passed off as coincidence, but the fact that there are so many indicate that there is some underlying mathematical explanation. If you know what that might be, why not leave a comment on the Plus blog?

Doubles

12 & 13 – 7 terms
14 & 15 – 15 terms
18 & 19 – 18 terms
20 & 21 – 5 terms
22 & 23 – 13 terms
34 & 35 – 11 terms
54 & 55 – 110 terms
60 & 61 – 17 terms
62 & 63 – 105 terms
76 & 77 – 20 terms
78 & 79 – 33 terms
82 & 83 – 108 terms
84 & 85 – 7 terms
86 & 87 – 38 terms
92 & 93 – 15 terms
94 & 95 – 103 terms
114 & 115 – 31 terms
116 & 117 – 18 terms
118 & 119 – 31 terms
140 & 141 – 13 terms
142 & 143 – 101 terms
148 & 149 – 21 terms
150 & 151 – 13 terms
162 & 163 – 21 terms
180 & 181 – 16 terms
182 & 183 – 91 terms

Triples

28, 29 & 30 – 16 terms
36, 37 & 38 – 19 terms
44, 45, & 46 – 14 terms
49, 50 & 51 – 22 terms
65, 66 & 67 – 25 terms
68, 69 & 70 – 12 terms
108, 109 & 110 – 111 terms
124, 125 & 126 – 106 terms
145, 146 & 147 – 114 terms
156, 157 & 158 – 34 terms
164, 165 & 166 – 109 terms
172, 173 & 174 – 29 terms
177, 178 & 179 – 29 terms

Quadruples

Quadruples are more rare than doubles, triples, and quintuples. The first quadruple is:

314, 315, 316 & 317 – 35 terms.

Quintuples

98, 99, 100, 101 & 102 – 23 terms
130, 131, 132, 133 & 134 – 26 terms

Post a comment on this story

---

Further reading

The following website contains some other methods that could be used for proving the conjecture. They are not sufficient as a complete proof, but definitely worth trying out!

• Physics Forum
• Samuel Jack