
A molecule's eye view of water
Water is essential for life on Earth, and it is a resource we all take for granted. Yet it has many surprising properties that have baffled scientists for centuries. Seemingly simple ideas such as how water freezes are not understood because of water's unique properties. Now scientists are utilising increased computer power and novel algorithms to accurately simulate the properties of water on the nanoscale, allowing complex structures of hundreds or thousands of molecules to be seen and understood.
"Using state-of-the-art computer simulation techniques we can now explain some of the mysterious properties of water such as how ice crystals grow, the structure of ice under high pressure or the behaviour of water in outer space. Understanding these particular processes of water has great relevance to important contemporary issues such as cloud formation and climate change, cryo-preservation of cells, and even the search for extra-terrestrial life!" says Professor Angelos Michaelides, London Centre for Nanotechnology and Department of Chemistry, University College London.
Normal ice has an underlying hexagonal structure, as the shape of a snowflake reveals. The hexagonal lattice is quite simple, but there are certain rules about how the water molecules pack inside the crystal that make ice much more complicated and interesting than we might expect.
A water molecule is made up of two hydrogen atoms bonded to an oxygen atom. The oxygen atom has two remaining pairs of electrons. These lone electron pairs and the hydrogen atoms are as far apart as possible, creating a tetrahedral arrangement. The oxygen lies at the centre of a tetrahedron (a three-dimensional shape made up of four identical equal-sided triangles) with the hydrogen atoms and the lone electron pairs in the direction of each of the corners.
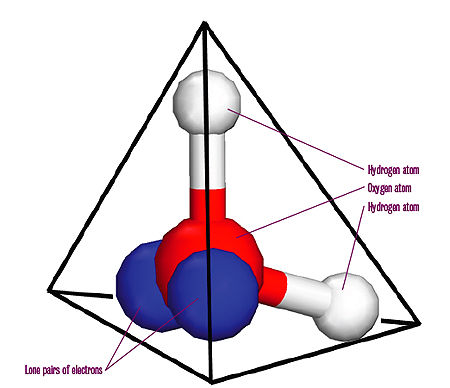
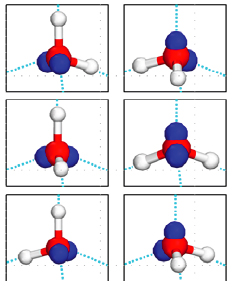
Water molecules in an ice crystal cannot fit together in any old way, because of their tetrahedral shape and the particular way they are held together. Using a branch of mathematics called combinatorics we can work out how many possible arrangements there are.
There are six ways of choosing two out of the four corners of the tetrahedron for the two hydrogen atoms. So there are a total of six possible orientations of a water molecule sitting within a larger ice crystal.
But not every potential arrangement of tetrahedra is possible, as each hydrogen atom of the water molecules must bond with a lone electron pair of an adjacent molecule. In fact, when the constraints of hydrogen-bonding are taken into account, the number of possible orientations for a given molecule is no longer six, but 3/2. Therefore, for a crystal of ice with N molecules there are (3/2)N possible ways to arrange the water molecules.
The ice cube in your drink has a volume of about 2cm3, containing about 6 × 1022 molecules. Our maths tells us that there are about (3/2)6 × 1022 ways that the water molecules could be arranged in that ice cube. That is more possibilities than the number of ways you could have drawn the lotto numbers every week since the Big Bang! Therefore, every single ice cube ever created will probably have a different arrangement of water molecules within it.
This article is based on the Maths Inside project, a collaboration of Plus and Mathematics Promotion Unit (run by the London Mathematical Society and the Institute of Mathematics and its Applications), in conjunction with the A molecule's eye view of water exhibit and the Royal Society. The Maths Inside project reveals the maths behind four specially chosen exhibits at the Royal Society Summer Science Exhibition. Click here to find out more about the project and to read articles accompanying other exhibits.
To find out more about A molecule's eye view of water visit http://www.chem.ucl.ac.uk/ice.
Comments
Anonymous
See, that's a weakness, saying there are 1-and-a-half ways of arranging something, without explaining how half a way is reasonable.
Anonymous
"In fact, when the constraints of hydrogen-bonding are taken into account, the number of possible orientations for a given molecule is no longer six, but 3/2. Therefore, for a crystal of ice with N molecules there are (3/2)N possible ways to arrange the water molecules."
how can there be a Fractional number of ways ? (3/2) ?
also, a crystal implies a regular array - not just the product of the one by one accumulations of molecules!
also: do you mean (3/2)^N or (3/2)*N ? - article seems to use both!
- without further explanation, the article's line of reasoning seems totally unreasonable!
Philip Bradfield - (retired) physicist/crystallography
philipbradfield2@gmail.com