We recently challenged our Twitter followers to a game: pick a positive natural number and if yours is the smallest number no one else has picked, you win. We are now pleased to announce that we've found a winner (who has been informed) and that the winning number is 6. Below is a histogram counting how many times the numbers up to 200 have been picked. There were a total of 127 responses, but for clarity the histogram misses out the 17 responses that were over 200 (142857 was the largest).

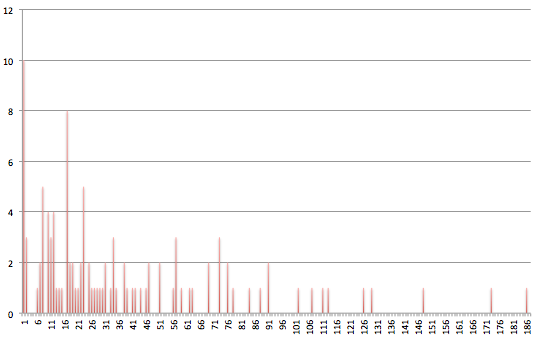
Should we be surprised by the result? The histogram shows that the number picked most often is 1 (picked ten times). This makes sense because it's the smallest natural number, but it's a bit strange it got picked so often: part of the objective was to pick a number that no one else would choose and 1 is the most obvious. Perhaps the pickers of 1 were being doubly clever, hoping that no one else would choose it because they'd reason that everyone else would. It's interesting to see, though, that the numbers 3, 4 and 5 didn't get picked at all, perhaps because people on the whole thought those low numbers were too obvious.

Following on the heels of 1 is 17, which has been picked 8 times. And after 17 come 8 and 23, each picked 5 times. It's interesting to note that both 17 and 23 are prime, perhaps reflecting people's attraction for prime numbers. Generally, all numbers that were picked more than once are less than 100, and most of them less than 50.

All this roughly reflects the musings of mathematician John D. Barrow (director of Plus) who has thought about this game in one of his books. Barrow noted that going for a very small number, like 1 or 2, won't do as others are likely to pick it too. Picking a very large one isn't a good strategy either, as it's very unlikely everyone else will have picked a larger one. So is there a winning strategy? Here is what Barrow says:

I don't know if there is a winning strategy but what the game picks up on is our reluctance to think of ourselves as "typical". We are tempted to think that we could pick a low number for some reason that no one else will think of. Of course, the reason why opinion polls can predict how we will vote, what we will buy, where we will go on holiday, and how we will respond to an increase in interest rates, is precisely because we are all so similar.

I have another suspicion about this game. Although there are an infinite collection of numbers to choose from, we forget about most of them. We set a horizon somewhere around 20, or about twice the number of people in the game, if it is larger, and don't think anyone will pick anything bigger than this. We then exclude the first few numbers up to about 5 on the grounds that they are too obvious for no one else to choose as well, and choose from those that remain with roughly equal probability.

A systematic study of preferences would involve playing this game many times over with a large sample of players (say 100 in each trial) to look at the pattern of numbers chosen and the winning choices. It would also be interesting to see how players changed their strategy if they played the game over and over again. A computer simulation of the game is not necessarily of any use because it needs to be told a strategy to adopt. Clearly the numbers are not chosen at random (in which case all numbers would get chosen with equal likelihood). Psychology is important. You try to imagine what others will choose. But the temptation to think that you don't think like anyone else is so strong that almost all of us fall for it. Of course, if there really was a definite strategy for picking the lowest number, everyone would be acting logically to adopt it but that would prevent them choosing a number that no one else chose, and they could never win with that strategy.

The above is an excerpt of Barrow's book 100 essential things you didn't know you didn't know, published by Bodley Head.