Plus Advent Calendar Door #16: Euler's formula

This article about complex numbers is a little advanced. Take a look behind yesterday's door for a basic introduction to complex numbers.

Many things in mathematics are named after Leonhard Euler, who probably was the most prolific mathematician of all time. In this article we explore a formula carrying his name which reveals a beautiful relationship between the exponential function and trigonometric functions. It also allows us to write complex numbers in an exponential way.

First of all, remember that a complex number has the form $x+iy$ where $x$ and $y$ are real numbers and $i$ is the square root of $-1$.

You can associate a complex number $z=x+iy$ with the point in the plane that has Cartesian coordinates $(x,y)$.

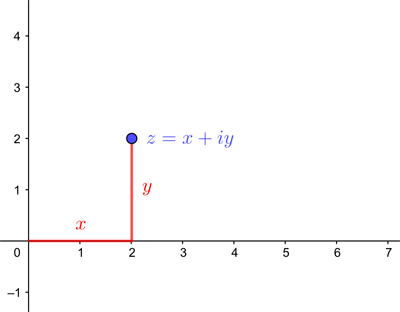
A complex number represented as a point on the plane in Cartesian coordinates.

Now a point $(x,y)$ in the plane can also be described by its polar coordinates $(r,\theta)$. Here $r$ is the distance from $(x,y)$ to $(0,0),$ and $\theta$ is the angle formed by the line connecting $(x,y)$ to $(0,0)$ and the positive $x$-axis (measured anti-clockwise).

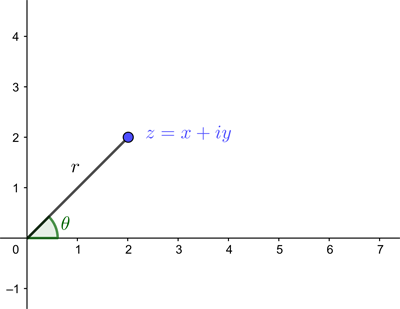
A complex number represented as a point on the plane in polar coordinates.

The relationship between the Cartesian coordinates $(x,y)$ and the polar coordinates $(r,\theta)$ can be worked out using a little trigonometry. It is $$x=r\cos{(\theta)}.$$ $$y=r\sin{(\theta)}$$

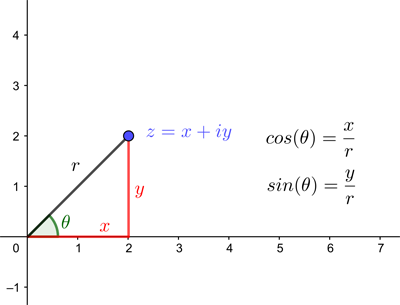
Trigonometry tells us the relationship between polar and Cartesian coordinates.

Going back to our complex number $z=x+iy$, we now see that it can also be written as $$z=x+iy=r\cos{(\theta)}+ir\sin{(\theta)}=r\left(\cos{(\theta)}+i\sin{(\theta)}\right).$$

Here comes the really interesting bit. We can also prove, using power series, that $$re^{i\theta} =r\left(\cos{(\theta)}+i\sin{(\theta)}\right).$$ You can find all the details of why this is true in our longer article on Euler's formula.

So, in summary, Euler's formula is that a complex number $z=x+iy$ can also be written as $$z=re^{i\theta},$$ where $$x=r\cos{(\theta)}$$ and $$y=r\sin{(\theta)}.$$ It is associated to the point in the plane that has Cartesian coordinates $(x,y)$ and polar coordinates $(r,\theta)$.

Euler's formula is beautiful in its own right, but it's also useful. It makes multiplying two complex numbers much easier. And of course it also leads to what's often described as the most beautiful equation in mathematics: Euler's identity:

$$e^{i\pi}+1=0.$$

We can see that the equation is true because $$e^{i\pi}+1=\cos{(\pi)}+i\sin{(\pi)}+1=-1+0+1=0.$$

People love this equation because it combines three of the most important numbers in maths — $0$, $1$, $e$, $\pi$, and $i$ — with three of the most important mathematical operations— addition, multiplication, and exponentiation. It almost feels like a miracle that these numbers and operations combine in such a beautifully elegant way.

You can read more about Euler's formula in our longer article. Or you can return to the Plus advent calendar 2021.

This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.