
Plus Advent Calendar Door #8: Counting infinities
An infinite set is called countable if you can count it. In other words, it's called countable if you can put its members into one-to-one correspondence with the natural numbers 1, 2, 3, ... . For example, a bag with infinitely many apples would be a countable infinity because (given an infinite amount of time) you can label the apples 1, 2, 3, ... and so on.
Two countably infinite sets A and B are considered to have the same "size" (or cardinality) because you can pair each element in A with one and only one element in B so that no elements in either set are left over. This idea seems to make sense, but it has some funny consequences. For example, the even numbers are a countable infinity because you can link the number 2 to the number 1, the number 4 to 2, the number 6 to 3 and so on. So if you consider the totality of even numbers (not just a finite collection) then there are just as many of them as natural numbers, even though intuitively you'd think there should only be half as many.
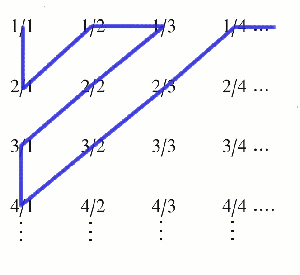
Something similar goes for the rational numbers (all the numbers you can write as fractions). You can list them as follows: first write down all the fractions whose denominator and numerator add up to 2, then list all the ones where the sum comes to 3, then 4, etc. This is an unfailing recipe to list all the rationals, and once they are listed you can label them by the natural numbers 1, 2, 3, ... . So there are just as many rationals as natural numbers, which again seems a bit odd because you'd think that there should be a lot more of them.
It was Galileo who first noticed these funny results and they put him off thinking about infinity. Later on the mathematician Georg Cantor revisited the idea. In fact, Cantor came up with a whole hierarchy of infinities, one "bigger" than the other, of which the countable infinity is the smallest. His ideas were controversial at first, but have now become an accepted part of pure mathematics.
You can find out more about all this in our collection of articles on infinity.