
The power of groups
"I am searching for abstract ways of expressing reality, abstract forms that will enlighten my own mystery." Eric Cantona, footballer.
The name of the game in pure mathematics is abstraction: by trying to pull back from individual problems, and instead look at their underlying structure, we develop more powerful tools with which to comprehend the world around us. Over a hundred years ago, mathematicians realised that many of the problems they were stuck on could be described by a single new structure: a group. Groups turn up all over the place, from chemistry to computer science. And the amazing thing — as we shall see — is that a single group can describe many, very different, problems.
From the particular ...
Before saying what exactly a group is, let's prepare the way by looking at two examples. The first thing to think about is the collection of all whole numbers: positive, negative and zero. You can add any two numbers to get a third, and this operation of addition never takes you into new territory: when you add two whole numbers you always get another whole number as a result. The process of adding the whole number a to something can be reversed without leaving the realm of addition: simply add the negative of a, the number -a, and you're back to where you started. This nicely self-contained system is an example of a group.
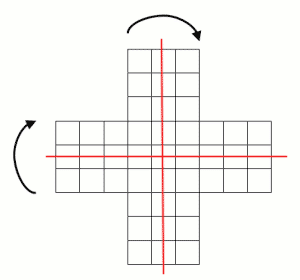
The second example is a little different: it's finite and instead of numbers it involves symmetries. The symmetries of a shape drawn on a piece of paper, like a square, are all those reflections and rotations that don't alter the appearance of the shape in the plane: unless you label the corners or edges, you'll never know if it's been rotated or reflected. For a square, the symmetries are the (clockwise) rotations through 90, 180 and 270 degrees about the centre point, the reflections in the horizontal, vertical and the two diagonal axes, and leaving the square fixed (not moving it at all).
Whenever you follow one symmetry by another, your overall movement is also a symmetry because the square appears unchanged. In the figure below you can see that a diagonal reflection, followed by a rotation by 90 degrees is the same as the reflection in the horizontal: combining two symmetries by doing one after the other never takes you out of the world of symmetries — just as combining two whole numbers through addition never takes you out of the world of whole numbers.
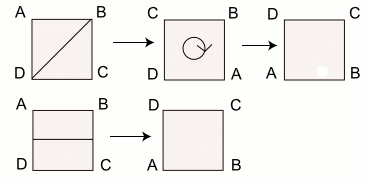
The first line shows a square first being reflected in one of its diagonals and then rotated clockwise through 90 degrees. The second line shows it being reflected in the horizontal axis — in both cases the square is left in exactly the same position.
Whenever you have performed a symmetry, you can undo it again: if you have rotated clockwise through an angle θ°, simply rotate clockwise through the angle 360 - θ°, and if you have reflected in a certain axis, simply reflect again in the same axis. There are exactly 8 distinct symmetries of the square, and together they form a neat little self-contained system. And they do so in a very similar way as the whole numbers do when considered together with addition.

Wield supreme power over your abstract universe!
What you've seen here is the same structure emerging from two, quite different, systems, and in fact there are many others where it turns up too (the real numbers with the operation of multiplication, or adding hours on a 24-hour clock are just two more examples). Capturing this structure, stripping it of all reference to a particular context, is what group theory is all about — and it gives mathematicians supreme power over all systems that carry this structure within them. So let's take a trip into the world of abstraction.
...to the general
Let me first introduce two key ideas. One concept that underpins group theory is that of a set. For us, a set is nothing more complicated than a collection of objects. For instance, this is a set containing three words: {apple, banana, cherry}. The figure below is a set containing three objects; an apple, a banana and a cherry. The objects contained in a set are called the elements of the set. There are infinite sets (like the set of all whole numbers) and finite sets (like the set of symmetries of a square). In this article we will only be concerned with finite sets: in this case we can list the elements, provided that the set is small.

A set is just a collection of objects. This set of three elements contains
an apple, a banana and a cherry.
A second concept that we need is that of a binary operation. This is a way of combining two objects to get a third. Addition and multiplication are both examples of binary operations (note that the third object you get from combining does not always have to be a new one, for example 2+0=2). Combining symmetries of a shape by doing one symmetry after the other is also a binary operation: you put two symmetries in and get a third one out. Many binary operations have inverses — ways of reversing the operation, as we've already hinted in our examples.
You're now ready for the formal definition of a group: a group is a set, along with a binary operation that can be applied to any pair of elements in the set (including any element and itself). When we work in the abstract, so that we have no particular name or symbol to give to the operation, we simply call it "multiplication" and use the symbol ×. The elements do not have to be numbers or symmetries, so the binary operation does not have to be addition or doing one symmetry after another. However, we are not allowed to make up the way in which the operation works in any way we like, it has to obey four rules called axioms:
Axiom 1: The product of any two elements from the set is another element of the set. That is, if a and b are elements of a group G, then a × b is an element of G too.
Axiom 2: There is a special element called the identity in the set. We often write e for the identity. It is the analogue of the number zero in addition or the number one in multiplication: if a is any element of a group G, then e × a = a × e = a. In our square example, the identity symmetry is simply doing nothing and leaving the square exactly as it is.
Axiom 3: The binary operation must be what is called associative. This means that it doesn't matter how we put brackets when we multiply: ((a × b) × c) = (a × (b × c)). Because of this axiom, we don't ever need to use brackets in a group. Addition and multiplication of numbers are both associative, but subtraction is not:
but
Thus we can't use subtraction as our binary operation to define a group.
Axiom 4: Our final rule requires that if a is any element of the group, then there exists a unique group element called the inverse of a, often written a-1, with the property that
where e is the identity element from axiom 2. The additive inverse of a positive number is the corresponding negative number :
We've already seen the inverses for the symmetry example.
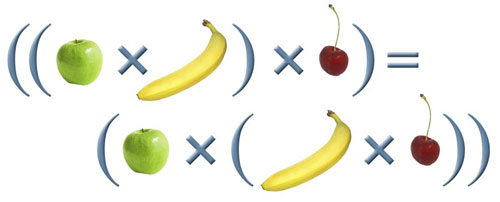
The binary operation must be associative: it doesn't matter where you put the brackets.
Alone with a group
I promised earlier that some potentially nightmarish problems can be solved quite effortlessly with a bit of group theory, and I'll now show you an example. The problem involves the game of Solitaire and the group that will help us solve it is one of the smallest there are: it's called the Klein 4-group after the mathematician Felix Klein.
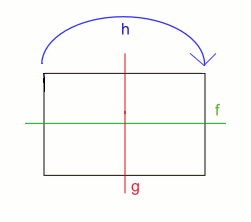
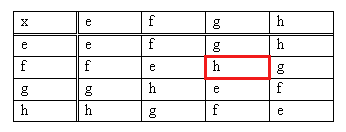
As the name suggests, this group has four elements and it describes, among other things, the four symmetries of a rectangle: reflection in the horizontal axis (we'll call this reflection f), reflection in the vertical axis (this reflection g), rotation through 180 degrees around the centre point of the rectangle (and this rotation h), and doing nothing at all (which we'll call e and which is the identity element from axiom 2).
The table below describes what happens when you follow one symmetry by another. For example, first doing f (reflecting around the horizontal axis) and then doing g (reflecting around the vertical axis) amounts to doing the symmetry h (rotating by 180°). This can be seen in the highlighted cell in the table, which is in the row labelled f and the column labelled g. Symbolically, this is represented by the expression f × g = h.
This group, seen as an abstract object, will be our main tool in solving a Solitaire problem that has nothing to do with the symmetries of a rectangle.
Lonely pursuits with groups
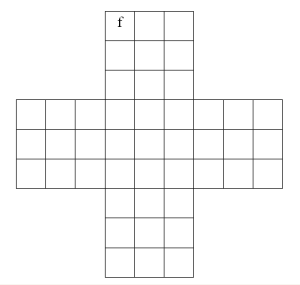
Solitaire, as its name suggests, is a game for one person. The board is in the shape of a plus sign, where each branch of the plus sign, as well as the centre, is composed of 9 holes arranged in a 3 × 3 square. At the beginning of the game, there is a counter, often a marble, in every hole except for the centre one.

That's (4 × 9) + (1 × 8) = 44 marbles in all. A move in the game consists of picking up a marble, and jumping it horizontally or vertically (but not diagonally) over a single marble into a vacant hole, removing the marble that was jumped over.
A marble cannot jump over more than one marble at a time, and cannot be jumped into a hole that already has a marble in it. The game is won by finishing with a single marble left on the board, in the central hole — that's the one that starts out as the only empty space.
Let's imagine that we just spent a frustrating afternoon, trying but failing to win at a game of Solitaire. We might try to make a new, easier, version of the game for ourselves, by saying that we'll count it as a win if we finish with a single marble anywhere on the board, rather than a single marble in the middle hole. The question is: would that really make the game easier?
It only would if it is actually possible to end the game with a marble in a hole other than the central one. There are zillions of possible sequences of moves that constitute a game. Checking them all by hand is completely and utterly unfeasible, so you need a clever way of tracking moves implicitly. Luckily there is one.

Can a group play Solitaire?
Klein-4 trickery
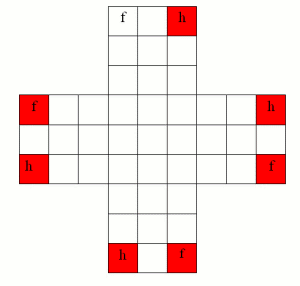
First we're going to label the holes of the board. We're going to label each hole with one of the elements f, g and h of the Klein 4-group, and we're going to require our labels to copy the multiplication of that group: for any three consecutive cells that lie in a horizontal or a vertical line, we require the labels of the first of these two cells to multiply together to give the label of the third.
It doesn't matter which labels we choose first, so suppose that we label the first two cells of the top row with an f and then a g. In the Klein 4-group we have
so the third cell in the top row must be an h. Suppose now that I label the first two cells in the second row with a g then an h. (I could have picked h and then an f, but nothing else would do. Why?) Then, using
we see that the third cell in the second row must be an f. Using these multiplication rules, along with
we can now fill in the whole of the rest of the Solitaire board to contain only equations from the Klein 4-group, like this:
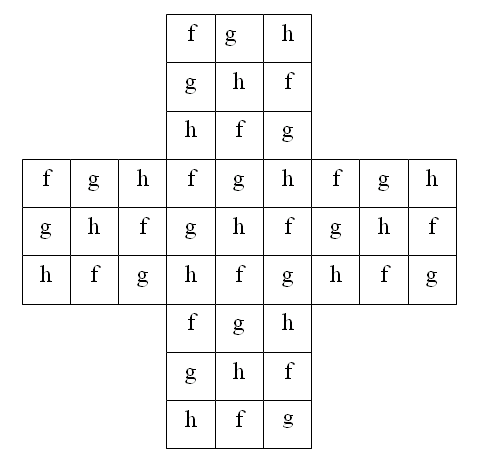
I'm now going to show you the main trick, that was told to me by a friend, Sinead Lyle, who's a maths lecturer at the University of East Anglia. It very cleverly uses the group's binary operation to solve our problem. At any stage in the game we define the total value of the board to be the element of our group that we get when we multiply together the labels of all of the holes that have marbles in them. For example, if there are only three marbles left, sitting in holes labelled h, g and f, then the total value is h × g × f = f × f = e.
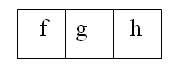
Because of the way we have set things up, the value of the board does not change when we make a move! To see this, remember that we labelled the top row with an f, a g and an h, like this:
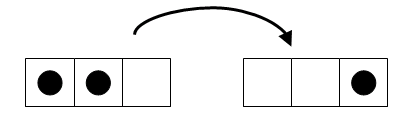
Suppose that at some point whilst playing Solitaire, we had a marble in the holes marked f and g, but none in hole h. Then we could jump the marble from square f to square h, removing the marble from square g.
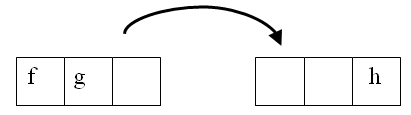
The value of the board was whatever the value was of the other 42 holes, multiplied by f and then by g. That is, the value of the board was whatever was in the rest of it, multiplied by f × g = h. The new value of the board is whatever is in the other 42 holes (which hasn't changed), multiplied by a single h. That is, the total value of the board has not changed as we made a Solitaire move. The value of the board when we finish playing must be the same as the value of the board at the beginning — and this, as we shall see, drastically reduces the number of possible finishing positions.
To work out the total value of the board at the beginning of the game, let's first see what the value would be if we put a marble in every single hole. Since the board consists of 5 squares and each square of 3 rows of 3 cells, the value of the whole board is the element you get when you multiply the individual values of the 5 × 3 = 15 rows of three cells. You can convince yourself pretty easily that each of these rows has value e. The very top row, for instance has value f × g × h = h × h = e. Putting all this together, the value of the board if we put a marble in every single square would be e multiplied with itself 15 times and this equals e.
At the beginning of the game there is no marble in the central square, labelled h. So the value at the beginning must be something that multiplies with h to give e. That's the inverse of h, namely h itself. So at the beginning of the game, the value of the board is h.
Now, recall that any time we make a move we preserve the overall value of the board. Therefore, at any point in a game of Solitaire, the value of the board must be h: this value never changes.
When there is a single marble left on the board, the value of the board is just the label of its hole. Therefore, returning to our "easier" version of Solitaire, this tells us that when there is a single marble left on the board, it must be in one of the holes labelled h. Thus we immediately see that only these 15 holes are possible finishing points for the game.
A Solitaire board is unchanged under reflection in the horizontal and vertical axes, and rotation through 90°, 180°, 270° and 360°.
But could we really finish in all 15 of those holes? If you look at the Solitaire board, it looks the same if we reflect it down a line through the middle column or the middle row.
Since there is nothing in the rules of Solitaire that distinguishes between right and left, or up and down, if we can get to a board position during the game, we can get to its mirror image under either vertical or horizontal reflection. Similarly, if we cannot get to some particular board position during the game, we cannot get to either its vertical or horizontal reflection. The board also looks the same if we rotate it by a quarter turn, a half turn, a three-quarter turn or a full turn, so if we cannot get to some particular board position, then we cannot get to the positions that are rotations from this point.
We have previously argued that we cannot finish with a single piece in the very top left corner, marked f, as the value of the board is always h.
Therefore, we cannot finish in any of its symmetric images. That is, we cannot finish in any of these eight holes (marked below), even though some of them are marked h.
Similarly, we cannot finish in the hole at the right-hand end of the third row, because it is marked g. Therefore, we cannot finish in any of its symmetric equivalents under reflection or rotation: the red holes marked on the following picture.
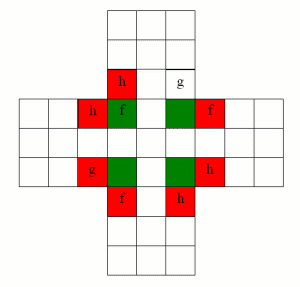
After using a similar argument (based on the f) to rule out the four green squares in the above picture, we are left with only 5 possible finishing places: the five holes labelled h that are only symmetric with other squares marked h. Four of them are equivalent to one another, the central hole is fixed by all symmetries.
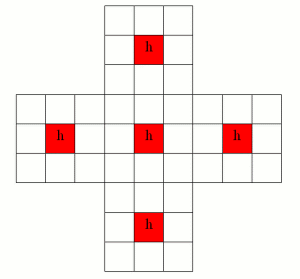
Now let us consider the hole labelled h in the top 3 × 3 square. Suppose we finished a game of Solitaire with a single marble in this hole. The only way that we could have finished with one marble here would be to have had two marbles before our last move, and these marbles must have been in the holes (marked f and g) that are directly below our current hole h. However, given marbles in those holes f and g, we might as well have jumped instead into the central hole marked h, the one that would make us win the "traditional" version of Solitaire.
Exactly the same argument shows that the other three holes marked h that are symmetrically equivalent to the one that we just considered are also foolish places to finish.
That is, our "easier" version of Solitaire turned out to be no easier at all!
If you've enjoyed following this argument, see if you can construct a similar one to show that finishing with two marbles might be a little bit, but not much, easier than finishing with one.
Hopefully, playing with this example will help you see how widely applicable group theory can be. As mathematicians, we use it to describe and analyse symmetry, and other scientists take this understanding of symmetry in the abstract and apply it to the real world. For instance, when chemists are analysing the structure of crystals, they know that individual crystals must have certain kinds of symmetry to enable them to stick together to form larger ones.
The symmetry operations of the
molecule PF5
As a working mathematician, identifying and using symmetry is what enables me to isolate properties of the mathematical world and see into the underlying structure that underpins our understanding and knowledge.
Further reading
You can read more about symmetry and group theory in chemistry in the past Plus article Through the looking-glass.
In 2020 Colva Roney-Dougal has been an organiser of a major research programme on group theory at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. You can find out more about group theory and the aims of this research programme here.

About the author

Colva is a lecturer in Pure Mathematics at the University of St Andrews. She initially went to university to do a degree in English and Moral Philosophy, but got distracted along the way and wound up with a maths degree. Since then she has worked at Queen Mary, University of London and the University of Sydney. She is interested in finite groups, computational methods and artificial intelligence.
Comments
Anonymous
There is an similar discussion based on Arie Bialostocki's 1998 article:
http://www.cut-the-knot.org/proofs/PegsAndGroups.shtml
Arie points out that, according to the game brochure (Milton Bradley Co., 1986), whoever succeeds in leaving the last peg in the center is a genius. Anyone who leaves a single peg elsewhere is an outstanding player. Quite a cause to stop and wonder.
Alexander Bogomolny
marcoslareo
Please help :-)
I have tried to find out the possible configurations with only two marbles left and I am finding that the number of those is quite larger than the five possibilities with only one marble left.
The article author writes that "finishing with two marbles might be a little bit, but not much, easier than finishing with one", which is not very precise.
My argument is based on the fact that the last two marbles left should occupy holes labeled "f" and "g" and then I start discarding possibilities based on the symmetry of the board. For example all the "f" and "g" holes that are converted into "h" by a symmetry will be discarded.
But I still get too many to agree with the author's words (sorry for not giving the total number in my count. I stopped the counting when I realized something must have been wrong).
Thank you,
Marcos
Anonymous
Instead of using the Klein group, I used the symbols 1 and 0, and added mod 2. Assuming this is legitimate, I could derive the same result about possible positions when one marble is left. For example, if the center hole has a 1 then there will be an odd number of 1's in the remaining holes, meaning that the sum is odd. All holes labeled 0 are eliminated as possibilities. Using the same type of symmetry arguments, there are only 2 types of position that do not have 0.
Anonymous
Wow, that was even better explanaton, thanks!
Anonymous
I follow your argument as to how the central hole is the only reasonable end point for the final ball.
However, your article promises to show how group theory can devise a strategy for solving the puzzle.
It does not do this.
I am sure that group theory really does have applications in chemistry but I have yet to see concrete examples.
Unfortunately, all the articles I read on this topic, including yours, merely give examples of symmetry in compounds and how this can be represented in terms of symmetry groups.
They go on to refer to how it is useful in interpreting IR and other spectroscopy but do not show how.
I was using spectra to deduce structures 60 years ago. The effect of chirality on polarized light has been known for a century.
And I hadn't heard of GT until last week.
I would be grateful if you could point me in the direction of articles showing how group theory adds to this.
Wally
Anonymous
Your article explains lucidly how GT shows that the centre hole in Solitaire is the only reasonable location for the last ball.
However, the article starts by saying it will show how GT can solve the puzzle.
It does not do this and I can't see how the process you outline, using GT, can achieve this.
Am I missing something?
walmo.walters@hotmail.co.uk
arbel
I think you are right
me
It's an existence proof - it shows
a) The puzzle has a solution
b) That the "easy" version is as hard as the centre hole problem.