Puzzle No. 2 - carnivorous beetles

Share this page
Submitted by plusadmin on 1 May, 1997
May 1997


Four carnivorous beetles awake from a good night's rest feeling agreeably hungry. These beetles are not too particular about their diets and will always move directly towards their prey at a constant speed of 1 cm/sec. It just so happens that this morning the beetle at point A wakes up looking directly at B, who is looking at C, who is looking at D, who is looking at A. The points A, B, C and D are at the corners of a square of sides 4 cms.

Beetles' starting position
Beetles' path

All the beetles wake up at the same instant and start moving towards their prey. Clearly they will follow a curved path because their breakfast is on the move too!

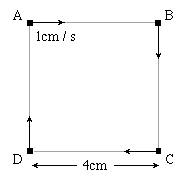
Diagram of problem

Does A catch up with B, and if so:

  1. How long does this take?
  2. How far does A move in this time?
  3. What happens?

We will publish the best solutions in the next issue, along with the answer to the problem itself.

Solution

  • Maths in a minute

    Want facts and want them fast? Our Maths in a minute series explores key mathematical concepts in just a few words.

  • Chocolate and mayonnaise
    chocolate

    What do chocolate and mayonnaise have in common? It's maths! Find out how in this podcast featuring engineer Valerie Pinfield.

  • From clicks to chords
    icon

    Is it possible to write unique music with the limited quantity of notes and chords available? We ask musician Oli Freke!

  • The lungs of the Earth

    How can maths help to understand the Southern Ocean, a vital component of the Earth's climate system?

  • SBIDER Presents: Shining a light on COVID modelling
    icon

    Was the mathematical modelling projecting the course of the pandemic too pessimistic, or were the projections justified? Matt Keeling tells our colleagues from SBIDER about the COVID models that fed into public policy.

  • Mathematical snapshots: Daniel Kreuter

    PhD student Daniel Kreuter tells us about his work on the BloodCounts! project, which uses maths to make optimal use of the billions of blood tests performed every year around the globe.