Tricky trig solution

We received quite a few correct solutions for this month's puzzle. In case it defeated you, the key was to look for symmetries in the information you are given, and to use similar triangles.

Part I

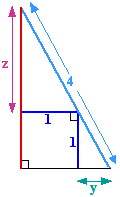
With $y$ and $z$ as in the diagram, $x=z+1$, so it is sufficient to find $z$. By similar triangles, $z:1$ as $1:y$, so $zy=1.$

By Pythagoras' Theorem, \begin{eqnarray*} (z+1)^2 + (y+1)^2 &= 16,\\ z^2 + 2z + 1 + y^2 +2y +1 &= 16,\\ (z+y)^2 - 2zy + 2z + 2y + 2 &= 16. \end{eqnarray*} But $zy=1$, so $$(z+y)^2 + 2(z + y) - 16 =0.$$ Solving this equation for $z+y$, and taking only the positive solution, yields $$z+y = \sqrt{17}-1.$$ Now we find $z-y$. $$ (z+y)^2 - (z-y)^2 = 4zy = 4,$$ \begin{eqnarray*} (z-y)^2 &=& (z+y)^2 - 4\\ &=& (\sqrt{17}-1)^2 - 4\\ &=&17 -2\sqrt{17} + 1 - 4\\ &=& 14 - 2\sqrt{17}. \end{eqnarray*} So $$z+y = \sqrt{14 - 2\sqrt{17}}$$ and \begin{eqnarray*} 2z &=& (z+y) - (z-y)\\ &=& (\sqrt{17}-1) - (\sqrt{14 - 2\sqrt{17}}) \\ &=& 5.52. \end{eqnarray*} Therefore $$x = z+1 = 2.76 + 1 = 3.76.$$

Part II

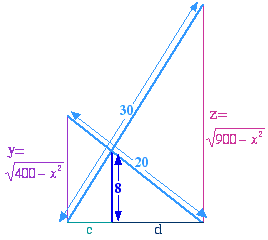
There are a number of approaches to this problem, but the one presented here follows from the observation that the information given is left-right symmetric - in other words, finding the two vertical heights will be equally easy (or hard!). We will label these two heights $y$ and $z$, as in the diagram.
By similar triangles, and dividing $x$ up into two segments $c$ and $d$, we see that $y:x$ as $8:d$ and $z:x$ as $8:c$; therefore $$z = 8x/c \mbox{ and} y=8x/d.$$ Adding gives $y+z = 8x^2/cd$ and multiplying gives $yz = 64x^2/cd.$ Combining these two results gives \begin{eqnarray*} yz &=& 8(y+z);\\ (y+z)/yz &=& 1/8;\\ 1/z + 1/y &=& 1/8. \end{eqnarray*} Leaving this equation to one side for a moment, we can use Pythagoras' Theorem to find each of $y$ and $z$ in terms of our unknown $x$, as shown in the diagram above. Combining these two expressions gives that $z^2 - y^2 = 500$.

Using Pythagoras' Theorem, we draw a triangle to represent this relationship:

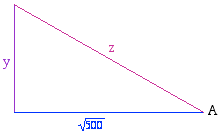
On its own, the information in this diagram is not enough to solve the triangle - for that, we would need one more bit of information. But now we can use the identity $yz = 8(y+z).$ All we have to do is find some combination of trig functions of $A$ that takes the form $1/z + 1/y$. Since $cos(A) = \sqrt{500}/y$ and $tan(A) = y/\sqrt{500}$, it is easy to see that $$ cos(A) + 1/tan(A) = \sqrt{500}(1/z + 1/y) = \sqrt{500}/8 = 2.7951.$$ Using a calculator gives $A = 27^o38^{\prime}30^{\prime\prime}$ and $z= \sqrt{500}/cos A = 25.24$. Therefore $$x= \sqrt{900 - (25.24)^2} = 16.2.$$