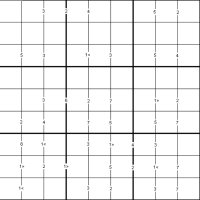
Duplex Difference Sudoku
Plus reader Henry Kwok has sent us his very own version of Sudoku, the puzzle that has sent half the world going into number fever. This is what it looks like; the rules are given below (you can download a PDF version of the puzzle and rules). The NRICH website will feature one of Henry Kwok's puzzles every month.

Rules of Duplex Difference Sudoku
This is a variation of Sudoku on a standard 9x9 grid which contains a set of special clue-numbers. These are small numbers placed always on the border lines between selected pairs of neighboring cells of the grid. Each clue-number is the difference between the two numbers that should be in the neighboring cells just to the left and to the right from that clue-number.
For example, a clue-number 7 on the border line means that one of the possible answers in the cell on the left can be 9, 2, 8 or 1. If we choose 9 for the answer in the cell, it means that the answer in the cell next to it on the right is 2. If we choose the answer 2, it means that the answer on the right is 9.
In addition, there are the symbols 1> and 1< on some of the border lines. The 1> means the answer in the cell on the left is 1 greater in value than the answer in the cell on the right. Similarly, the 1< would indicate that the answer in the cell on the left is 1 less than the answer in the cell on the right.
The remaining rules are as in a standard Sudoku: the object of the puzzle is to fill in the whole 9x9 grid with numbers 1 through 9 (one number per cell) so that each horizontal line, each vertical line, and each of the nine 3x3 squares (outlined with the bold lines) must contain all the nine different numbers 1 through 9.
If you are stumped by last issue's puzzle, here is the solution.
For some challenging mathematical puzzles, see the NRICH puzzles from this month or last month.