
From quasicrystals to Kleenex
The motto of the Nasrid kings who built the Alhambra of Granada was "God is the only victor". Allah is all-powerful: the Qur'an forbids the depiction of living beings in religious art lest it be seen as a blasphemous attempt to rival the creative powers of God. To avoid this, artists created intricate patterns to symbolise the wonders of creation. The repetitive nature of these complex geometric designs suggests the infinite power of God.

Decoration from the Alhambra. © Octavo corporation (www.octavo.com)
The Nasrid, the last of the Muslim dynasties in Spain, constructed in the Alhambra some of the finest examples of this mathematical art. This sprawling citadel, looming high above the Andalusian city, boasts a dazzling array of mosaics, with tiles arranged in beautiful, intricate patterns, and is a testament to the beauty of mathematics.
The Alhambra tilings are periodic: they consist of some basic unit which repeats itself in all directions to fill up all the available space. Periodic tilings can theoretically continue indefinitely. That is, they can be used to cover even the whole plane, a mathematical flat surface that goes on forever in all directions. There are seventeen classes of periodic symmetry and examples of thirteen of these classes can be found in the Alhambra. See Steve Edwards' site at Southern Polytechnic State University for examples of these tilings and a discussion of symmetry classes.
Many single shapes can tile a plane periodically (a square, for instance, can be used to tile the plane in chequerboard fashion). Some shapes can also tile the plane aperiodically - so that the pattern never repeats itself. For example, the diagram shows (part of) a tiling using 2-by-1 rectangles or domino shapes. Although the tiling is mainly periodic, a few tiles have been placed differently from the others, wrecking the periodicity; the whole tiling is aperiodic.
![[APERIODIC TILING USING DOMINOES]](/issue16/features/penrose/domino.gif)
On the other hand, the domino shape could, obviously, also be used to create a periodic tiling. It is more difficult to find a set of tiles that tile only aperiodically. Indeed for many years it was believed to be impossible. However, in the 1960s mathematicians began to devise sets that tiled only aperiodically, an area of mathematics that is beyond the reckoning powers of computers. All calculations must be done by hand, which would put off most people, but the most famous set of tiles was invented purely for fun, by Oxford professor Roger Penrose.
![[IMAGE: Ascending and Descending]](/issue16/features/penrose/escher.jpg)
M.C. Escher's "Ascending and Descending"
© 2001 Cordon Art - Baarn - Holland (www.mcescher.com).
All rights reserved. Used by permission.
Penrose, who was knighted in 1994 for his services to science, is best known for his work on relativity theory and quantum mechanics, having shared the 1988 Wolf Prize for Physics with Stephen Hawking. His use of mathematics is not confined to his work - one of his hobbies is solving and devising geometrical puzzles. With his late father, the geneticist L.S. Penrose, he invented the "Penrose Staircase", which seems to go on climbing forever, even though it goes round in a circle and comes back on itself. By exploiting the laws of perspective they realised an actual 3-dimensional model could be made, which projected this illusion if viewed from the correct angle. The Dutch artist M.C Escher used the Penrose staircase in his lithograph "Ascending and Descending" (right).
There is no such optical trickery in the Penrose tiles, but they are as beautiful and fascinating as any of Escher's prints. Penrose first developed a set of six tiles in 1973 and then "began thinking about reducing the number; and by various operations of slicing and re-gluing, I was able to reduce it to two". There are several forms of Penrose tilings, the most elegantly simple consisting of two rhombs, a thick one and a thin one, with rules as to how they should be aligned (otherwise, obviously, a single rhomb could be used to make a periodic tiling). The dimensions of the rhombs and the rules for aligning them are shown below. All angles are multiples of θ = π/5.
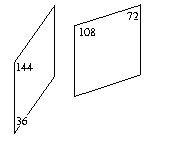 All angles are multiples of 36 degrees (π/5) |
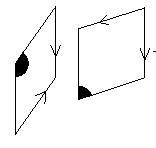 Two adjacent vertices must be of the same colour. Two adjacent edges must have arrows pointing in the same direction or no arrows at all. |
Following these rules, the tiles can be grouped into vertex stars (a set of tiles which share the same vertex). The first two vertex stars are made by using five of the thick rhombs, with the black vertices on the inside in the first set and on the outside in the second. Without the vertices marked, the two vertex stars look the same; however by following the rules it turns out the thin rhombs can only be tiled around them in certain ways. The other vertex stars use different arrangements of the thick and thin rhombs. In total there are only eight possible combinations.
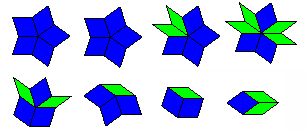
The eight vertex stars allowed in the Penrose rhomb tiling.

The first two look identical without the rule markings, but force the surrounding tiles to be placed differently.
To prove that only these combinations are allowed, we can characterise each vertex star by a cycle of integers from the set {1,2,3,4,}, referring to the measures of the angles, in multiples of q, that meet at the vertex. For example, the sixth vertex star in the diagram above is characterised as (2,2,2,4).

If we want to tile other rhombs around this vertex star, we must use a combination of rhombs that will fit the boundary vertices. Starting with the top vertex and moving clockwise, we can see that this vertex star has partial boundaries with multiples of q� 2;3,3;2;1,3;4;1,3;2;3,3.
We must therefore use stars containing these boundaries to fill in all the gaps. For example if we wish to add tiles to the bottom right hand corner we need a combination which contains the partial string 1,3. The only vertex star which contains this string is the star characterised as (1,2,1,3,3), the fifth star in our atlas of vertex stars above. Aligning tiles according to the rules, we find that we do indeed get the cycle corresponding to this star.
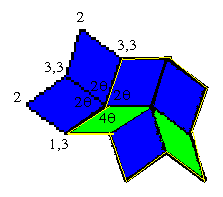
We can show this similarly for each of the vertices in turn, and for all of the stars - for a more detailed description, see Marjorie Senechal's "Quasicrystals and Geometry" (Cambridge University Press, 1995).
Each of the vertex stars will appear infinitely often in any Penrose tiling, with the ratio of thick to thin rhombs at 1.618:1, the "golden ratio" which has been considered beautiful in mathematics since ancient times. All the pieces fit together to cover a flat surface, but the pattern does not repeat at regular intervals - some parts of the pattern could be periodic on local scales, but the whole pattern, although it may look periodic at first glance, is not periodic. Such order within disorder is known as quasiperiodicity.
If the pieces are tiled together correctly, a Penrose tiling can continue forever. But efforts to complete a tiling come unstuck if pieces have been put together incorrectly initially: after a while, it becomes impossible to place pieces correctly. Penrose has joined forces with a US company called Pentaplex, which uses his tilings to make fiendishly difficult board games.
Recreational maths aside, the tilings have applications beyond board games. Geologists had always thought that all crystals had a simple, periodic arrangement, but in 1982 Israeli crystallographer Dan Shechtman discovered quasicrystals: metallic substances which are crystalline but do not follow the usual rules of crystal structure. It took him two and a half years to get his results published, because the establishment refused to believe that such renegade crystals could exist.
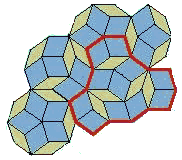
Quasicrystals exhibit unusual symmetries, which geologists had always thought were impossible in nature, but it turns out that quasicrystal structure can be explained by a form of Penrose tiling. Clusters of adjacent atoms (outlined in the schematic diagram, left) overlap according to specific rules, analogous to Penrose's tiling rules, giving the materials their unusual structure.
Quasicrystalline materials are more than just a geological curiosity - their resistance to wear means they could have many practical applications. One close to home is that they make excellent non-scratch coating for frying pans.
Penrose tilings have also been put to rather different use: in 1997, Kleenex used a form of the rhomb design on their quilted toilet paper. The unrepeating pattern of the Penrose tiles, as well as being attractive, allowed thicker paper to be rolled up without bunching. Sir Roger was less than impressed when his wife returned from the supermarket with the offending tissue, and promptly sued the company. David Bradley, director of Pentaplex, commented that it was common for large companies to ride roughshod over small businesses or individuals, but "when it comes to the population of Great Britain being invited by a multi- national to wipe their bottoms on what appears to be the work of a Knight of the Realm without his permission, then a last stand must be made".
See also
- Ron Lifshitz's page on Quasicrystals
- Quasitiler (a program to generate Penrose tilings)
Thanks to Aoife Donnelly and Barry O'Donovan.
About the author
![[Alison Boyle]](/issue16/features/penrose/alison.jpg)
Alison Boyle began life as a physicist, with a degree from the National University of Ireland, Galway. She then pursued a Masters in Astronomy before deciding that her mission in life was to write about science, rather than actually do it. She is currently finishing up an M.Sc. in Science Communication at Imperial College, London. After this she is hoping to finally abandon the student life and find a job as a science journalist.