
A richer view of the inside
Our ability to see inside a person's body, without surgery, has revolutionised modern medicine and saved countless lives. And each life saved is thanks to the mathematics of tomography. This medical imaging technique passes waves through a person's body, mathematically reconstructing an image from the amount these waves are scattered or absorbed by the structures inside.
Tomography is also used for many other non-medical purposes – from electron tomography of viruses and microchips to muon tomography of volcanoes. Tomography using X-rays is used in engineering and materials science, and has applications in airport security screening and archeology. Neutrons, light, radio waves and sound can all be used to see inside of objects using the mathematics of tomography.
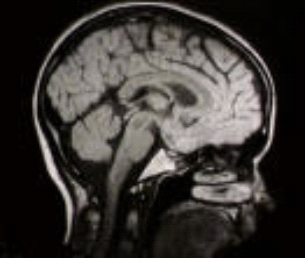
A CT scan of the inside of a head.
All of these applications, medical and non-medical, involve imaging by sections. Usually in tomography you measure a line integral, which you can think of as the sum of all the contributions along a line from the waves that pass through the object that is being imaged. For example in computerised tomography (CT) high energy X-rays pass through a person's body in a straight line, with the intensity of the X-ray reducing by different amounts as it passes through different types of tissue. The intensity of the X-ray as it leaves the body is measured, representing the accumulation of the effects of the different tissues along that line through the body. The data for a CT scan consists of many of these line integrals measured along different angles and positions through the body, with one number, one scalar, measured per line. (You can read more in Saving lives: the mathematics of tomography.)
"But for rich tomography we measure more than a scalar," says Bill Lionheart, from the University of Manchester. Instead of measuring a single number for each line, in rich tomography you could make more complex measurements, perhaps represented by an array of numbers (a matrix), or a diffraction pattern. Then the aim is to reconstruct something with a richer structure from these measurements. Rather than a digital image of an object, which consists of numerical pixel values, you might want to construct an image of the strain in an object, which has multiple-dimensional tensor values at each point.
New data needs new maths
Lionheart is one of the organisers of a research programme on Rich and Nonlinear Tomography (RNT) at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The programme brings together the mathematicians and statisticians working on these problems, with the engineers, physicists and clinicians producing and using this tomographic data. "The numerical analysts provide essential knowledge to numerically solve the problem, but they are also working in an interdisciplinary way with the people who own the problem," says Lionheart. "So perhaps slightly unusually for a Newton Institute programme we have quite a few people who are not mathematicians coming to explain their problems... so that we can learn new problems and communicate the mathematical solutions we have to them."
There is an ever increasing volume of data that is being collected by sensors, across a wide range of sensing areas, says Francis Watson, also from the University of Manchester and one of the organisers of the programme. And this ever increasing data is outpacing the increasing speed of computers. "So we need to not just wait for computers to catch up, but we need to be mathematically much smarter."
For example, the next generation of space or airport radars are going to capture volumes of data equivalent to the internet bandwidth of a city like Edinburgh, says Watson. "That's vast. But not only are [the developers of these radars] increasing this amount of data, they want these radars to interoperate together in a distributed way." This means the data from these new radars will no longer fit the assumptions used to mathematically reconstruct the information captured by the previous radar. "We need to interact with radar specialists to understand what we can do for them mathematically."
These new types of data being collected by these new sensors require new mathematics. "Sensors are increasingly capturing data in multiple dimensions," says Watson. "The mathematics isn't actually available [yet] to understand what information is contained in this data, and how we solve the inverse problem which extracts [this information]."
Challenges
"Most tomography problems are actually non-linear," says Lionheart. "And that of course makes them much harder to solve both in theory, and numerically." Linear problems (such as y=2x) are nice and predictable – if you double the input you double the output. But non-linear problems are much more complicated and can even exhibit chaotic behaviour. (You can read more about non-linearity in this accessible introduction, and how you might try to tackle non-linear problems in Model behaviour.)
Not only that, the mathematical problems involved are also ill-posed, meaning that there can be more than one solution to a problem. "That means that the relationship between the data and the actual image is extremely challenging," says Romina Gaburro, from the University of Limerick, and another organiser of the programme. Extracting information from images can often lead to ill-posed problems, as suggested in the image below. "You need a rich wealth of data at hand [to solve such problems," says Gaburro.
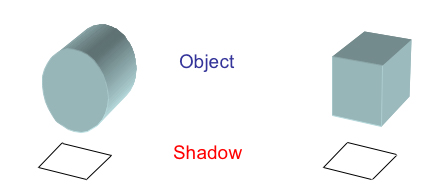
Determining the shape of an object by it's shadow can be an ill-posed problem: both a cylinder and a cube could cast the same shadow. (Image by Chris Budd from Inverse problems save the day)
The challenge also comes from having so many different communities engaging with the inverse problems that lie at the heart of rich nonlinear tomography, each with their own different point of view. Gaburro says that the programme aims to bring these different communities together, "perhaps to find a common language between medical doctors, geophysicists and mathematicians, to try to solve these problems that are extremely challenging but also extremely useful."
As well as mathematical and theoretical challenges, there are also computational challenges of developing new and efficient algorithms that can deal with these rich nonlinear problems, says Silvia Gazzola, from the University of Bath and another organiser of the programme. "The application may demand quick answers... [But] simply using some off-the-shelf standard algorithm can get you into trouble when you're trying to solve problems with good accuracy, in a quicker way. So there is a need for a new algorithm that can take the mathematical theory and take the data and give us reliable answers."
Collaborative possibilities
"As many of our inverse problems involve electromagnetic or acoustic waves, the interaction of waves with complicated media is of great importance," says Lionheart. " This is why it is so fortunate that the RNT programme coincides with other research programmes at the INI: one on multiple wave scattering (MWS – you can read more about this area here) and another on data-driven engineering (DDE). "Our colleagues in MWS specialise in modelling the interactions of waves with matter and numerical solutions of the wave equation. The DDE programme [covers] a probabilistic approach to inverse and [related] problems. RNT has had a fertile interaction with its sister programmes with participants attending each other’s seminars and workshops."
One of the strengths of the INI is bringing people together from so many different mathematical areas. Lionheart recalls: “One week towards the end there was a short programme on operator algebra that I thought at first that would have little relevance. On the Tuesday I was explaining random matrices to my PhD student in the context of image reconstruction in radar. Then I realised that random matrix theory is now part of [another area of mathematics] invented by Dan Voiculescu to solve problems in algebra. The next day I realised he was attending the operator algebra workshop and was able to meet him”. Sometimes even the most seemingly unrelated mathematics has unexpected connections.
About this article
This article was based, in part, on the interview below, produced by Dan Aspel from the INI, with Bill Lionheart, Silvia Gazzola, Francis Watson, Romina Gaburro, and Sean Holman, the organisers of the INI programme Rich and Nonlinear Tomography – a multidisciplinary approach. Click here for all our content related to this INI programme.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
