Geoff Tennant teaches mathematics at Mill Hill School, Muswell Hill, North London. He also acts as a consultant for TV productions designed for mathematics teaching.

I recently attended a Masters course in Mathematics Education, having obtained a Mathematics degree and then taught for some years. During the course, two problems came up which caught my attention. The first was to consider throwing a die repeatedly until obtaining a 6, and to note the number of throws this took - it could be as few as 1, or it could, theoretically, carry on for ever. If one repeated this, say, 1000 times, and then drew a bar chart showing the number of times it took 1, 2, 3, 4, ....., throws, what would the bar chart look like? You may like to consider this problem before proceeding!

My own line of reasoning went like this. I had come across the problem before, but not in quite this form. I knew that the mean number of throws required is 6. My bar chart therefore looked like this (figure 1):

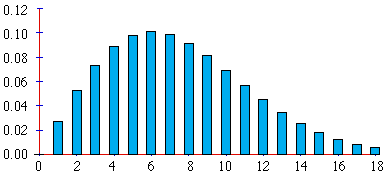
Figure 1: the author's guess at the form of the probability distribution
for the die throwing problem.

In fact, the solution is quite different. The probability of getting a 6 on the first throw is 1/6. The probability of getting a 6 on the second throw entails not getting a 6 on the 1st, and so is (5/6)*(1/6). The probability of getting a 6 on the third entails not getting a 6 on the first or second, and so is (5/6)*(5/6)*(1/6), and so on. The bar chart therefore, actually looks like this .

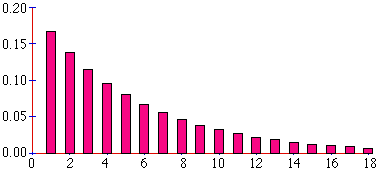
Figure 2: the actual probabilities of throwing a six at throw n.

It made me feel better that everyone in the room - all teachers, mostly secondary mathematics teachers - got it wrong. But my solution rested on the idea that the mean equals the mode of a distribution. This is, of course, true for the Normal distribution, but is most definitely not true in general or in this particular case. Now I know that this isn't necessarily true, I have taught children this using appropriate examples, but, faced with an apparently simple and unfamiliar task, I find myself reverting to this idea. What is going on?

The other problem I faced during the Masters course was the Taxi Problem, which is considered elsewhere in this magazine. This came up in some preparatory reading, and for a good two months I wrestled with the problem on and off, tried to get some A-level Pure and Statistics students onto it (who simply suggested multiplying the probabilities), other teachers, advice stations on the Internet...... When I finally did get given a solution, my overwhelming reaction was relief at seeing how it's done. But mixed in with that was a considerable measure of frustration - the solution requires no mathematics which isn't well within my grasp, so what was the problem?

In this case, I realised very quickly that the solution was not obtainable simply by multiplying the probabilities - considering the extreme cases of increasing one or other of the probabilities to 1 confirms that - but I approached the problem with the mindset that the only two ways of combining two probabilities in anything like a straightforward way is either to add them or multiply them. Since neither applied, I found myself unable to consider the problem from a different angle.

It is good, I think, for teachers to put themselves into learning situations of this nature once in a while, to remind ourselves of the kinds of feelings that our pupils can have when things are not proving straight forward.

In addition, though, in thinking through my reactions to these problems, and drawing on my experience as a Mathematics teacher, I would like to propose a simple 4 step model for mathematics learning:

I have learnt something if:

1. I understand it while it's being explained to me;
2. I can do closed ended exercises on it;
3. I can explain it to somebody else;
4. I am able to apply it out of context in an unfamiliar situation.

Further I would suggest that attached to each of these learning steps are methods of teaching:

1. lecturing;
2. closed ended exercises;
3. asking questions along the lines of, "What did we do last lesson?" or peer group teaching;
4. going on to another topic in which the original subject is only a small part, or investigational work / problem solving.

Take negative number arithmetic as an example. In my experience as a secondary teacher, it is not difficult to get children to feel they understand what is going on from Year 7 onwards. It is not much more difficult to get them to do closed ended exercises and to explain what is happening in terms of temperatures, bank balances, etc - although whether they can still do it next week is another question! The real difficulty comes when negative numbers are part of algebraic problems - substitution, simultaneous equations and the like - when much of what has been learnt goes completely out of the window. And how many children would choose to use negative number arithmetic in an investigation of their own, if it was an appropriate thing to do?

Going back to the original two problems, I can use my model to assess my own status as a learner on the ideas I got stuck on. As an experienced teacher, I was able to get to step 3 without problem, having explained these ideas to other people. What I couldn't do was use these ideas in an unfamiliar situation, reverting, unconsciously, to beliefs I haven't had consciously for many years.

It seems to me that this model can be used to explain some differences in international standards. Countries which do well in comparison tests are, it would seem, those who concentrate their teaching and learning on points 1 and 2 - a lot of whole class teaching and repeated practice, at the expense of actually using the material learnt. This is certainly in accordance with my own experience of dealing with children newly arrived from Africa, who knew their times-tables backwards (and even better forwards!) and could do simple arithmetic without problem, all beautifully written out. But as soon as they were in anything approaching an unfamiliar situation, they would glaze over and be unable to cope.

In this country, however, we can be reluctant to make much use of whole class teaching (or lecturing) and quite a number of texts in current usage are really quite short on actual hard practice of concepts. We are good, however at the discussion, problem solving and investigational work, and indeed, "Using and Applying Mathematics" represents 1/5 of the National Curriculum.

Is not the danger in this approach, however, that we are trying to get children to run before they can walk? That children are supposed to be applying concepts - which I would suggest is a very sophisticated skill, and not one that I've fully mastered as I've already outlined! - before they've fully assimilated them. And can I further suggest that what often passes for "Using and Applying" as defined by the National Curriculum, is in reality the considering of a small number of problems using a very narrow range of mathematical skills.

So where does that leave us? In my opinion, our emphasis on discussion, problem solving and relevance is a great asset in this country, but it must not be at the expense of repetitive practice and, dare I say it, drill. Once children have thoroughly learnt a topic they are then, hopefully, in a position to apply it.

Let me finish by referring again to my own experience. Despite having all the necessary mathematics at my fingertips, I failed to solve two problems presented to me. Now that I've seen the solutions and been able to confront my failure, is not my mastery stronger than before?

Geoff has written to us separately about the taxi problem that he mentioned above. See his letter on the Letters page.