Solution to Puzzle No. 2 - carnivorous beetles

For the question see " Puzzle No. 2 - carnivorous beetles", in issue 2.

At first sight it may appear necessary to write down the equations of motion of the beetles as a set of differential equations and to solve these to find the paths or trajectories. However, as with our first puzzle there is a trick (see "Solution to Puzzle No. 1 - the ring").

Solution

The problem is symmetrical so we can see straight away that whatever paths the beetles take they will always be at the four vertices of a square whose origin remains fixed.

We know that A's path must curve because B is also moving. From the direction of B's motion we can also see that A's path must curve towards the interior of the square. So the square is shrinking (as well as rotating clockwise).

Notice that the component of B's velocity in the direction of AB is always zero so the length of the side from A to B is shrinking at the speed at which A is moving towards B, 1cm/s. After 4s the square has shrunk to a point with all the beetles having spiralled into the centre.

To summarise: A takes 4s to catch B and travels 4cm in this time. As to what happens, that is left to your imagination!

Solution using calculus:

Writing down the equations of motion for the beetles and solving them is another way of working out what happens. It also tells us something that is not obvious from a simple plot of the beetles' paths.

Take origin O as the centre of the square, and consider the motion of the beetle at corner A. Work with polar coordinates as shown in the diagram with r as the distance OA. Then:

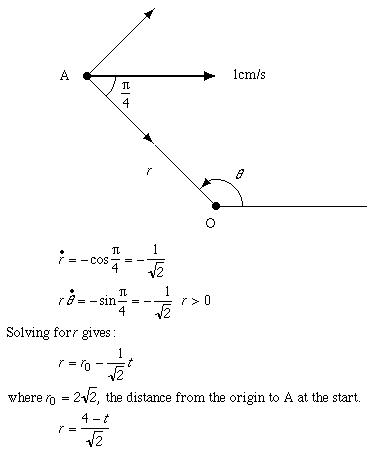
From this we see that the beetles must eventually collide at t = 4 which gives us our answer.

It is also instructive to solve the equation for theta.

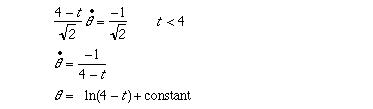
Notice that as t gets closer to 4, theta gets larger and larger without bound. In other words the beetles spin around each other an infinite number of times before colliding.