Solution to "Yet more taxis!"

To solve this problem we can extend the technique we used in Issue No 2. To make our working easier to read, let's define $k$ to be the number of possible colours other than blue. That is, $k$ = $n-1$. For convenience, we'll label the other colours $C_1-C_k$. \par Consider 100 possible cases (contingencies), in which taxis are involved, in proportion to their numbers. Each case is equally probable. We expect 85 cases to involve blue taxis, the other 15 cases being equally distributed between the $k$ other colours. \par If a blue taxi were really involved, the witness will report blue with probability 80\% or some other colour, say $C_1$, with probability 20\% divided by $k$. If a $C_1$ taxi were really involved the witness will report blue or some other colour, say $C_2$, with probability 20\% divided by $k$ and $C_1$ with probability 80\%. \par The number of times that these outcomes are expected to occur in each case can be shown in a contingency table. The following table only contains entries for blue, $C_1$ and $C_2$ but the pattern should be obvious.

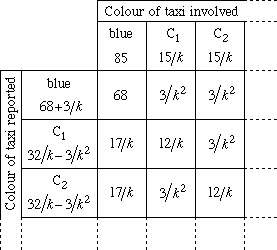
So, given that the witness reported seeing a blue taxi, we must use the row in the table corresponding to the reported blue taxi.

The probability that the taxi was blue is therefore:

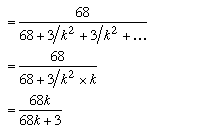
This is simply the number of cases in which the witness reported a blue taxi and was right, divided by the total number of cases in which the witness reported a blue taxi. \par If we let $k$ equal 1 in this expression we simply get 68/71, which is of course the same result we got for the blue/green case. Notice that as the number of taxi firms increases the probability that a blue taxi really was involved in the accident gets closer and closer to 100\%. \par Now let's look at what happens if the witness reports some other colour, say $C_1$. What is the probability that a $C_1$ taxi really was involved? \par This time we use the row in the table corresponding to the reported $C_1$ taxi. The probability that the taxi was $C_1$ is therefore:

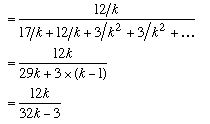
If we put $k$ equal to 1 again we get the (perhaps) surprising result of 12/29, which is just 41\%. Clearly the witness's evidence is of very little value. Notice also that as the number of taxi firms increases the probability that a $C_1$ taxi was involved in the account {\em decreases} towards 37.5\%. Having more firms actually weakens the evidence still further. The reason for this "paradox" is that the mistaken sightings of other taxis are swamping the small number of correct identifications.