Split reflections

Whether you are checking someone out in a mirror or bouncing the eight-ball off the cushion to win at pool, the law of reflection is one of the handiest tools you can pick up from physics. The law of reflection says that a wave or stream of particles (or indeed a pool ball) is reflected off a boundary at an angle equal to the angle with which it hit the boundary - but is it always? Scientists at Harvard have shown for the first time that light reflected off the surface of a chiral liquid not only bounces back at a different angle, but is also split in two.

Light misbehaves in a chiral liquid.
(Image courtesy of Peer Fischer and
Ambarish Ghosh)

Light normally behaves in a very predictable way. Shine a light at a mirror and the angle at which it hits the mirror (called the angle of incidence) will be equal to the angle at which it is reflected off the mirror (the angle of reflection) — it obeys the law of reflection. When light passes from one material to another, such as when you shine a light into a swimming pool, the ray is bent as it enters the water, because the light travels at a slower speed in the water than in the air. The amount it is bent is governed by Snell's law:

where n_i are the refractive indices of the two materials, indicating how much light is slowed down by these materials. The principles of reflection and refraction of light can be explained by Fermat's principle — that light will always take the quickest path to reach its destination. (Read more about how to derive the Law of Reflection and Snell's law from Fermat's principle, and find out about other materials that affect the behaviour of light in Light bends the 'wrong' way.)

Light is split by a chiral liquid.
(Image courtesy of Peer Fischer and
Ambarish Ghosh)

Peer Fischer and Ambarish Ghosh from the Rowland Institute at Harvard, have show that light behaves very differently in liquids made up of chiral molecules - molecules who are not mirror images of themselves. Instead chiral molecules come in two versions, called enantiomers, one left-handed, and one right-handed. Many naturally occurring molecules are chiral (you can read more about them in Through the looking-glass). A liquid is chiral if the number of left- and right- handed enatiomers are not equal, and the liquid will behave in different ways depending on which enantiomer has the upper hand. Fischer and Ghosh used limonene, which as the name suggests, has links with lemons. One enantiomer is found in the rind of citrus fruit and is responsible for the citrus smell, while the other enantiomer instead has a piney smell.

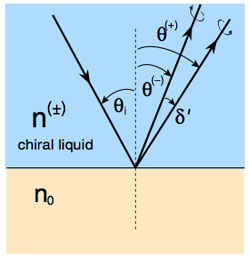
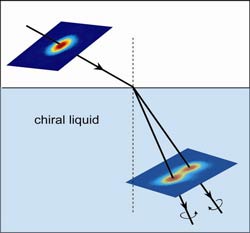
When they looked at how light in the chiral limonene (i.e. either the lemony left-handed version, or the piney right-handed one) was reflected, they saw that the reflected beam was split in two. The reflected beams bounced off at slightly different angles, and the angle of reflection for either beam was not equal to the angle of incidence. Light in limonene did not obey the law of reflection. Similarly odd behaviour occurs for refraction: light passing into the chiral liquid again splits into two beams, each refracting at a different angle.

This effect was predicted nearly 200 years ago by the French mathematician Augustin Fresnel, one of the founders of the wave theory of light. Fresnel studied optically active materials — materials which affected the polarisation of light. He predicted that a light beam entering an optically active liquid would be split into two beams, one left-circularly polarised light (the electric part of the light wave rotates clockwise around the direction the light is travelling) and one right-circularly polarised (electric field rotates counter-clockwise), each a different angle of refraction.

Fresnel knew that there were two types of the optically active liquid, each circularly polarising light in different directions. He didn't know why materials were optically active, but we now know that in liquids (in the absence of a magnetic field) it is a hallmark of chiral molecules. "This is good news as liquids are important to chemists and biologists," says Fischer. "Hence, natural optical activity, including optical rotation in liquids, immediately tells us that the structure of the molecules has to be chiral. In conjunction with theory one can even determine the handedness of the molecule. "

Similar behaviour had been observed in
some chrystals, but the tiny divergences
in chiral liquids meant that it had never
been seen in those media before.
(Image courtesy of Peer Fischer and
Ambarish Ghosh)

However Fresnel's prediction of refraction in chiral liquids, and further predictions of reflection in chiral liquids, had never been measured before now. But it is not that surprising given the tiny differences in the split beams that had to be detected.

"The divergence between the beams was at best a few microradians," says Fischer. "This means that the center of the light beam has moved by one micron a meter away. (The thickness of hair is typically around 70 microns). The sensitivity of the detection scheme (which finds application in a variety of fields such as laser tweezers) is phenomenal — it can resolve angles as small as a few tens of nanoradians. This corresponds to an angle subtended by the top and bottom of a house as seen from the moon."

Using a complicated set up to magnify the divergence, and highly sensitive detectors, Fischer and Ghosh were able to observe the splitting of light as it was refracted by the chiral limonene. They also managed to detect that when light in a chiral liquid reflects off the boundary it is split into two beams as well, both reflecting at different angles to the angle of incidence — the first time light has been observed defying the law of reflection.

The researchers hope that the work will provide ways of ascertaining chirality of liquids, and even their handedness, using only tiny samples. But don't worry, as long as your table isn't in a chiral pool, you can still rely on your winning pool shot.