
Through the looking-glass

Through the looking-glass
When Alice stepped through the looking glass in Lewis Carroll's Through the Looking-Glass and What Alice Found There, she would have found that more than just the writing was back to front. The very molecules that made up her body would have been the wrong way around in the looking-glass world, and their
interaction with the looking-glass molecules would have led to a very confusing - and possibly dangerous - adventure!
Symmetry has always played an important role in our world. We have an innate aesthetic appreciation of symmetry - we prefer symmetrical faces, and find naturally occurring symmetry in flowers and reflections beautiful. And when we choose asymmetry it is usually because we recognise the effect that the absence of symmetry produces.

Our appreciation of symmetry in ourselves is not surprising, considering that it may be an indication of health and survival prospects (see Reflecting on extinction in Issue 20). In fact, considerations of symmetry are important at the very smallest scale - symmetry or the lack of it in the molecules of which we and everything around us consist has a fundamental effect on their behaviour and our existence. Mathematics has given chemists the tools they need to quantify symmetry, allowing them to classify molecules and understand their behaviour better.
Mirror, mirror...
To see an obvious example of asymmetry, just look at your hands. Your left and right hands are mirror images of each other, and the only way you can make your left hand look like your right is to look at it in a mirror - moving or turning it just won't work. A molecule that, like your hands, cannot be made to look like its mirror-image by rotating it or displacing it, is called chiral. As with hands, chiral molecules can occur in two different forms, called enantiomers, which are mirror-images of one another. One will be thought of as the left-handed one, and the other the right-handed one, though it is not always clear which should be which.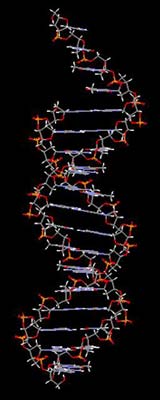
DNA, the blue-print for our whole body, is chiral.
Chiral molecules play an important role in chemistry in general, and in particular in the chemistry of life, as the majority of molecules involved in living organisms are chiral. The most famous is DNA - the information carrier inside our cells that contains the blue-prints for the structure of our whole body. The DNA structure is a double helix looking something like a twisted ladder. The two cross-linked helices are always right-handed, twisting in the same direction as a normal screw.
Interestingly, chiral molecules that occur naturally almost always occur only in the left-handed or the right-handed enantiomer, rather than in both forms. The reason for this may be to preserve energy. Molecules are transformed in living organisms by enzymes - huge organic molecules with cavities that enclose other molecules like a glove, allowing a chemical reaction to take place. Chiral molecules, just like our hands, need the right sort of glove. So they need to be transformed by chiral enzymes with the same handedness, just as you need a right-handed glove for your right hand. If both enantiomers of the chiral molecule occurred naturally, organisms would have to produce both versions of the enzyme, which would require a great deal more metabolic energy than if only one sense of chirality was necessary.
However, when chiral molecules are manufactured synthetically in a lab using ingredients that are not chiral, the resulting enantiomers will be present in equal numbers. For many applications, including pharmacology, the two enantiomers need to be separated, which is not a simple process. As they have different physical properties and may react differently with the chiral molecules in the human body, the presence of both in pharmaceuticals could have disastrous consequences. It is thought that Thalidomide - used in the 1950s to control morning sickness during pregnancy - may be an example. The drug contained both enantiomers, and although one did indeed suppress morning sickness, its mirror image may have caused the many birth defects that resulted from its use.
Not just smoke and mirrors
With chiral molecules we have been thinking of symmetry in terms of whether an object is identical to its mirror image. However, we also have an intuitive feel for other kinds of symmetry. For example, we know that a circle is somehow more symmetrical than a equilateral triangle. If you rotate both through 120° clockwise around their respective centres, they will appear unchanged, but if you rotate them through 90°, the triangle will now look different. In fact, you can rotate a circle around its centre by any amount and it will still look the same - it possesses complete rotational symmetry. We intuitively understand that the more things you can do to an object - the more planes in which you can reflect it, the more ways in you can rotate it - without changing its appearance, the more symmetrical it must be.
Mathematically, we break down the symmetry of an object into those types of operations we can perform on the object without changing its appearance - called the symmetry operations. For example, for a smiley-face a reflection through a vertical line down its centre is a symmetry operation. And each operation has a corresponding symmetry element, which is the imagined line, plane
or point around which a symmetry operation occurs - such as the vertical line down the middle of the smiley-face that the reflection occurs with respect to.
When examining symmetry in the three-dimensional world, there are four types of symmetry operations to consider: rotation, reflection, roto-reflection and inversion.
Rotation
The rotation symmetry operation rotates an object about an axis. Some objects are symmetric under any rotation - for example, a circle can be rotated by any amount around its centre and still look the same - whereas others are only symmetric under repeated rotations around some axis through (360/n)° for some number n. For example, rotating the cross-shaped handle of a tap by 90° about an axis through its centre - as you would to turn the tap on - is a symmetry operation. Repeating the rotation gives another symmetry operation - if the original rotation was by (360/n)°, then there will be n rotations before the object is returned to its original position.
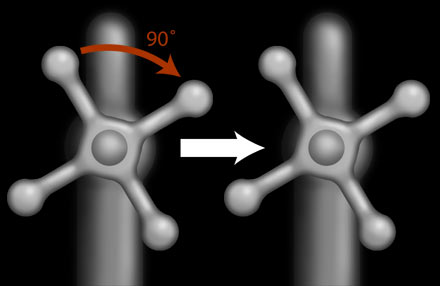
Turning the tap through 90° is a symmetry operation
There can be more than one rotation axis for an object, and if so the one with the most rotations before it returns the object to its original position will be called the main axis of rotation. A dumb-bell, for example, has infinitely many axes of rotation. The main one passes through the weights at each side, along the bar which an athlete grips - and every rotation around this axis is a symmetry. Any line through the dumb-bell's centre of gravity, perpendicular to the main axis, is also an axis of rotation. There are only two symmetric rotations around each of these axes - through 180° and 360°.
Reflection
The reflection symmetry operation, as you might expect, reflects an object with respect to a plane. If the plane contains the main rotation axis then it is usually called a vertical reflection plane; and if it is perpendicular to the main rotation axis it is known as a horizontal reflection plane.For the dumb-bell, any plane containing the main rotation axis is a vertical reflection plane, and there is a horizontal reflection plane cutting the dumb-bell in half through its centre of gravity, perpendicular to the main rotation axis.
Roto-reflection
This symmetry operation is not as immediately obvious as the more familiar rotation and reflection. The roto-reflection operation involves two steps - rotating an object by (360/n)° about an axis and then reflecting it with respect to a plane perpendicular to the axis (the axis is the symmetry element for this operation).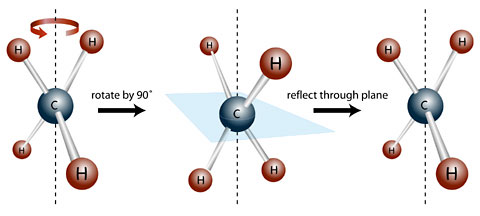
The rotoreflection symmetry operation combines rotation and reflection
Like rotations, roto-reflections can generate a number of symmetry operations. However, unlike normal rotation, the number of operations generated depends on whether n is even or odd. Also, as for rotation, there can be more than one roto-reflection axis.
Inversion
The inversion operation, i, takes every point in an object to a equidistant point on the other side of the centre of inversion (the symmetry element). It can be easier to understand if you think of the centre of inversion as the point (0,0,0) - then the inversion operation takes every point (x,y,z) to (-x,-y,-z). For example, a dumb-bell is symmetric under inversion in its centre of gravity.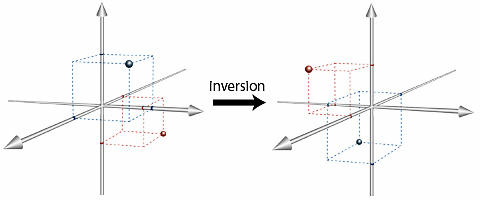
Any object, indeed any molecule, will contain at least one of these symmetry elements - the operation C1 known as the identity operation - a rotation of 360 °, the equivalent of doing nothing. Things start to get interesting when a molecule has more than C1.
The mathematics of symmetry
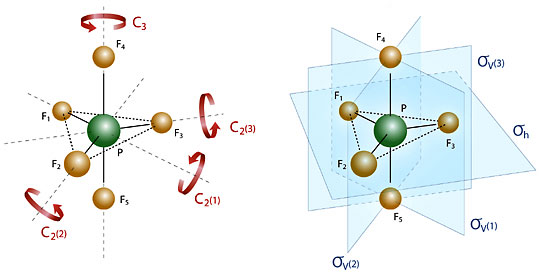
The symmetry operations of PF5
The molecule PF5 is an interesting example as it has many different symmetry elements. The main axis of rotation is a three-fold rotation axis (labelled C3) which contains the fourth and fifth F atoms and the P atom. The molecule also has three two-fold rotation axes (labelled C2(1) to C2(3)) each containing the P atom and one of the other F atoms. PF5 also has three vertical planes of symmetry (labelled σv(1) to σv(3)) and a horizontal symmetry plane (σh). Finally, there is also a three-fold rotoreflection axis coincident with the main axis of rotation.
We will write C31 and C32 for rotation through 120o and 240o around C3 respectively, and use the notations C2(1) to C2(3), σv(1) to σv(3) and σh for both the symmetry elements and the associated symmetry operations.
Multiplication and identity
If we rotate the labelled PF5 molecule about the C3 rotation axis, and then reflect it in one of the symmetry planes, say σv(1), the molecule will end up in exactly the same position as if we had only reflected it in the σv(3) symmetry plane. So we can write thatwhere o is the symbol for composition of operations, and the operation applied first goes on the right hand side.
In any molecule, successive application of the symmetry operations it admits will always result in another symmetry operation on the molecule, allowing us to think of combining the operations as a kind of multiplication. Since C1 has no effect on the molecule, multiplying any symmetry operation by C1 results in the original symmetry operation. So for multiplication of symmetry operations, the identity operation C1 acts just like the number 1 in normal multiplication.
Associativity and inverses
And just as for normal multiplication, where $1\times (2\times 3)=(1\times 2)\times 3=1\times 2\times 3$, it doesn't matter where you put the brackets when multiplying symmetry operations. As we can see in the molecule ${\rm PF}_5$: $$ C_3^{1} {\rm o} (\sigma _v(1) {\rm o} \sigma _h) = C_3^1 {\rm o} C_2(1) = C_2(2); $$ $$ (C_3^1 {\rm o} \sigma _v(1)) {\rm o} \sigma _h = \sigma _v(2) {\rm o} C_2(1) = C_2(2). $$This property of multiplication is called associativity, and it holds true for all the symmetry operations for every molecule.
Sometimes, multiplying two symmetry operations gets you back to the identity symmetry operation $C_1$. For example, reflecting in a symmetry plane twice returns an object to its starting position - the equivalent of applying $C_1$. The same is true of rotating first by $120^{\rm o}$ and then by $240^{\rm o}$. Two such operations are said to be {\em inverse} to one another. And again just like normal multiplication of non-zero numbers, where for every number there is another that multiplies with it to equal 1 ($n \times 1/n = 1$), there is an inverse for every symmetry operation.
It's a group thing
So there is an analogy between the collection of symmetry operations on an object, and normal multiplication on non-zero real numbers. And this is because both are examples of an important mathematical concept - groups. A group is just a set of things - for example, the symmetry operations on a molecule, or the collection of integers - on which is defined some associative operation, such that there is an identity element and every element has an inverse in the group. For example, the collection of integers under addition is a group (the identity element is 0), and groups occur throughout mathematics from geometry to combinatorics to cryptography. The application of group theory to chemistry is just one of its uses outside of mathematics - another is in the error-correcting codes used to create the no-scratch feature of CD players (see the Coding theory: the first 50 years from Issue 3 for more information).
The symmetry operations on a molecule constitute a mathematical group, called a point group by chemists because there is always one point in space - not necessarily on one of the atoms - left unchanged by every symmetry operation in the point group. By determining the point group for a molecule, chemists are able to classify it and deduce important infomation about its structure and how it will behave.
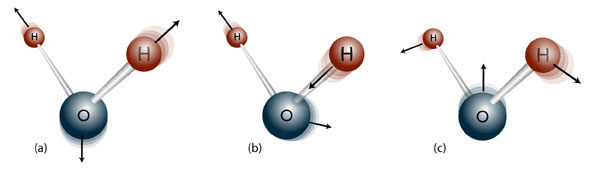
The three vibration modes of water under infra-red radiation
One application is in molecular spectroscopy, where compounds are bombarded with radiation such as infrared light, causing the molecules to vibrate as they absorb the energy. The point group of the molecule being analysed helps chemists to interpret the spectrum they see as a result of these vibrations. For instance, when a water molecule is exposed to infra-red radiation the resulting
spectrum will show peaks at certain energies which correspond to particular motions of stretching and bending of the O-H bond (called vibration modes). Another molecule with the same point group will experience the same number of vibration modes, though not at the same frequency due to a number of factors including the different weights of its constituent atoms.

How would you like to live in Looking-glass House, Kitty? I wonder if they'd give you milk, there? Perhaps Looking-glass milk isn't good to drink...
Whether we are talking about highly symmetrical inorganic molecules or the chiral molecules of biology, the mathematics of symmetry has given chemists a tool to help understand their structure and behaviour. In fact chirality and symmetry are a driving force in all chemistry, and in defining our very nature and the world we live in. The looking-glass world Alice entered would indeed be a very different place, with mirror-image DNA and enzymes and amino acids, meaning that - as Alice suggested to her kitten - looking-glass milk would almost certainly not be good to drink. Its mirror-image molecules would all be the wrong way around for her enzymes to digest, as would the molecules of all the food in the looking-glass world.
So, were Alice to have stayed too long on the wrong side of the mirror the mirror, she would most likely have paid the ultimate price for her adventure, and starved to death!
Further reading
Reflections on Symmetry: in Chemistry and Elsewhere, by E. Heilbronner and J. Dunitz, is a beautifully illustrated book explaining the role symmetry plays in our lives, including a discussion of the impact of symmetry on Alice's adventures through the looking-glass.The 2001 Nobel Prize in Chemistry was won for work with chiral molecules.
The Point Group Tutorial from Emory University, has 3-D models of molecules and their symmetries.
Read more about the development of group theory from the University of St Andrews
Comments
Manshu Prajapti
Science is not everyone's cup if tea. All you need is to put your all effort and mind in it. By the way it was amazing post for science lover.