
Time and motion

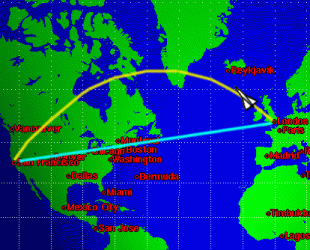
Figure 1: The blue route?
But speed isn't the only consideration in travel: it's also important to make sure that the route chosen is the shortest. Imagine you were piloting Concorde from London to San Francisco, and you had to choose a route on the map. Would you choose the straight line, marked in blue, or the long curved line marked in yellow? Well the curved line is the shortest one!
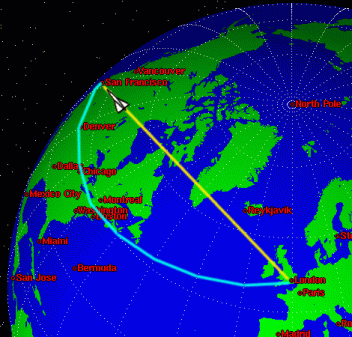
Figure 2: Or the yellow?
Why's that? It's because the Earth isn't flat, but maps are, so maps are always distorted. The shortest route between two points on a globe is along part of a great circle, which is a large circle going all the way round the globe with the centre of the Earth at the centre of the circle. You can see on the picture of the world why the great circle route (in yellow) is shorter than the route which looked straight on the flat map. (You can imagine the yellow line as being part of a bigger circle going all the way round the Earth - or you can convince yourself by looking at a toy globe!)
In general, on a surface that isn't flat, a line between two points on the surface which is as short as possible is called a geodesic. On the Earth, all geodesics are parts of great circles.
Calculating the distance
How do we calculate the great circle distance between two airports? It's important to know how far it is so that the airline companies know how much fuel to load onto their planes! It's easy to work it out using ideas of longitude and latitude, and the scalar product (also called the dot product) of two vectors.
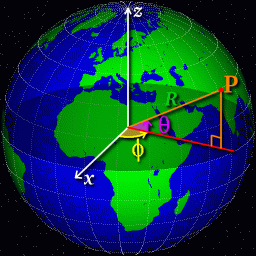
Figure 3: Latitude and Longitude
Think about a point $P$ on the Earth's surface, with latitude $\theta$ (measured North from the equator) and longitude $\phi$ (measured East from the Greenwich meridian). We'll assume that the Earth is a perfect sphere of radius $R$, where $R$ is about 6370 km (though it's possible to do the calculation taking into account the fact that the Earth isn't exactly spherical).
Its easy to see that the $z$-coordinate of the point $P$ is $R\sin\theta$; a little more thought shows that its $x$ and $y$ coordinates are $(R\cos\theta)\cos\phi$ and $(R\cos\theta)\sin\phi$. So for two points on the Earths surface, their position vectors relative to the centre of the Earth are $$ r_1 = \left( \begin{array}{c} R \cos \theta_1 \cos \phi_1 \\ R \cos \theta_1 \sin \phi_1 \\ R \sin \theta_1 \end{array} \right)$$ and $$ r_2 = \left( \begin{array}{c} R \cos \theta_2 \cos \phi_2 \\ R \cos \theta_2 \sin \phi_2\\ R \sin \theta_2 \end{array} \right)$$ We can therefore calculate the dot product $$ {\bf r}_1{\mathbf.}{\bf r}_2 = R^2(\cos\theta_1\cos\theta_2(\cos\phi_1\cos\phi_2+\sin\phi_1\sin\phi_2) +\sin\theta_1\sin\theta_2). $$ But there is another formula for the dot product: ${\bf r}_1{\mathbf.}{\bf r}_2 = |{\bf r}_1| |{\bf r}_2| \cos\alpha$ where $\alpha$ is the angle between the vectors. So $$ \alpha=\cos^{-1}\biggl({{\bf r}_1{\mathbf.}{\bf r}_2\over R^2}\biggr). $$ Now we use the well-known formula for the length of an arc of a circle: it is $R\alpha$, as long as we measure $\alpha$ in radians. So now we know the distance along the great circle route!
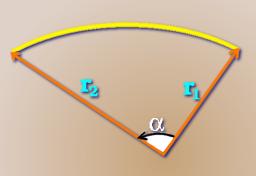
Figure 4: Alpha
London to San Francisco
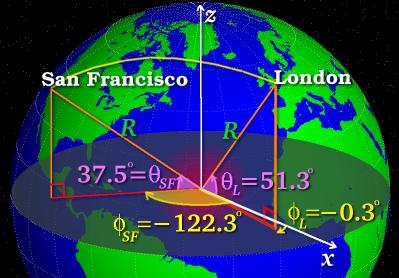
Figure 5: LHR to SFO
London Heathrow airport has latitude $51.3^\circ$~N, so $\theta_1$ is $51.3^\circ$, and longitude $0.3^\circ$~W, so $\phi_1$ is $-0.3^\circ$ (negative because Heathrow is West of the Greenwich meridian). For San Francisco, $\theta_2=37.5^\circ$ and $\phi_2=-122.3^\circ$. Putting these values into the formulae gives $\alpha$=1.36 radians, so the distance is 8640 km to three significant figures.
Look up some locations in an atlas and work out the distances between them - for example, you could work out the distance from your home town to London. Does it differ much from the distance you'd get if you just measured it on a map? Would the same happen for all pairs of locations?
The real routes that aeroplanes take aren't always the great circle ones, for various reasons. There are sometimes problems with flying over other countries' airspaces. Wind speed and direction make a difference as well: it can be quicker to deviate from the great circle route in order to pick up a beneficial tailwind!
If you'd like to plot your own great circle routes there's a nifty page at gc.kls2.com which does just that. The same site has a useful help file on the subject.
Travelling at the speed of light?
Einstein's theory of relativity tells us that it's impossible for us (or anything else that has a mass!) to travel at the speed of light. But at the dawn of the new Millennium, some people are determined to try - after a fashion!
The inhabited land area which will first officially see a dawn on the 1st of January, 2000, is Pitt Island, east of New Zealand in the Pacific Ocean. As the Earth turns, the Sun will rise in each country in turn going West. Some intrepid travellers plan to be in the Pacific for the sunrise and then fly West at just the right speed so that the Sun is always just rising on the horizon behind them. Of course they're not really travelling at the speed of light, but from where they are it'll look like they're managing to stay ahead of the Sun! For them, it'll be dawning on the Millennium continuously for 24 hours.

Figure 6: Pacific sunrise
How fast would they need to fly to accomplish this? Fortunately it turns out to be a sensible speed! If they were flying around the equator, they would need to travel the circumference of the Earth, a length $2\pi R$, in 24 hours, which works out to be a speed of 1670 km/hr (or 464 m/s). This is faster than the speed of sound, but Concorde could do it! A better idea is not to travel
round the circumference but round a smaller circle on the Earth, staying at constant latitude, and then they wouldn't need a supersonic aeroplane. Good luck to them!
About the author

Dr. Robert Hunt is the Editor of PASS Maths. He is a Lecturer in the Department of Applied Mathematics and Theoretical Physics at Cambridge University, and a Fellow of Christ's College.