Tricky arrangements

If you've ever had to make a time table of some sort, you'll know that it's not an easy task — which is why combinatorics, the art of arranging things according to certain rules, constitutes a whole field of mathematics in its own right. It's in this field that mathematicians have recently made a bit of a breakthrough. They've found particular arrangements some people thought didn't even exist. The structures involved are quite abstract, but they may have practical applications in communications technology.

The best way to understand the new discovery is to start with a puzzle. Suppose you have a group of nine people. Each day they go out for a walk in groups of three. Can you arrange the people so that in four days of walking no two people are in the same group more than once?

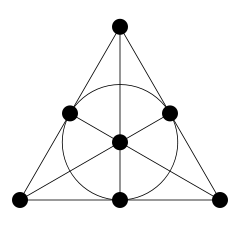
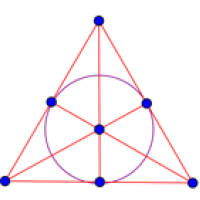
The solution is here if you want to see it. It forms what is called a Steiner triple system: an arrangement of $n$ objects (in the example $n=9$ and the objects are people) into triples so that no two objects appear in the same triple more than once. The picture on the right shows an $S(2,3,7)$ Steiner system. There are seven points and seven lines (we count the central circle as a line too). Each line contains three points and every pair of points only appears on one line. In other words, the lines define triples of points so that no pair of points occurs in more than one triple. More generally, a Steiner system $S(t,k,n)$ is an arrangement of $n$ objects into groups of $k$ so that no set of $t$ objects appears in the same group of $k$ more than once.

One question you can ask about Steiner systems is for which values of $t$, $k$ and $n$ they exist. It's intuitively clear that not any old combination of numbers will do, and indeed there's a divisibility condition: for a $S(t,k,n)$ Steiner system to exist certain numbers that depend on the values of $t$, $k$ and $n$ must exactly divide each other (see the box). An important result from 2014 by the mathematician Peter Keevash showed that this divisibility condition is good enough as long as the number $n$ is sufficiently large: if $n$ is large enough and the divisibility condition is satisfied, then a $S(t,k,n)$ Steiner system definitely exist.

The new result involves a generalisation of Steiner systems. Instead of a collection of $n$ objects, think of a string of $n$ zeroes and ones (computers use strings like these, hinting to a connection to information technology). For $n=3$ examples of such strings are $(1,1,1)$ and $(1,0,1)$. The collection of all such strings for a given $n$ form what is called a vector space (we won't define vector spaces here in detail, you can look up the definition using the link). Let's call this vector space $F_2^n$: the $2$ indicates the number of different symbols that appear in our strings (only zeroes and ones) and the $n$ indicates the length of the strings. Every vector space comes with a dimension: in our example it's the number $n$, the length of the string.

Just as a collection of $n$ objects has sub-collections consisting of a smaller number of objects, so a vector space of dimension $n$ can contain a smaller vector space of a smaller dimension. Which leads us to a question analogous to our Steiner system question above: given the vector space $F_2^n$, a number $t$ and a number $k$, can you find a collection of $k$-dimensional subspaces of $F_2^n$ so that each $t$-dimensional subspace of $F_2^n$ is contained in exactly one of the $k$-dimensional subspaces? If such a system exists, it's called $S_2(t,k,n)$. (It is also possible to form vector spaces with the number $2$, which in our example tells us that only two symbols appear in our strings, replaced by another number $q$. In this case the vector spaces are denoted by $F_q^n$ and the corresponding Steiner systems are called $S_q(t,k,n)$.)

Until recently mathematicians thought that interesting examples of systems of the form $S_q(t,k,n)$ might not even exist. It's this prediction that Michael Braun, Tuvi Etzion, Patric R.J. Östergård, Alexander Vardy and Alfred Wassermann have proved wrong. In particular, they found several different systems of the form $S_2(2,3,13)$.

"The search was challenging because of the enormous size of the structures [involved]," says Östergård. "Searching for them is a gigantic operation even if there is very high-level computational capacity available. Therefore, in addition to algebraic techniques and computers, we also had to use our experience and guess where to start looking, and that way limit the scope of the search."

Mathematicians will be pleased, simply because the result solves a long-standing problem. But there's also a surprising practical angle. The communications industry relies heavily on error correcting codes: the idea is to encode a message in such a way that even if errors slip in during transmission, these errors are automatically ironed out (see Take a break and Communication and ball packing to find out more). It turns out that $S_q(t,k,n)$ systems provide optimal codes for a particular technique of error correcting. "Our discovery will not become a product straight away, but it may gradually become part of the internet," says Östergård. The new result has been published in Forum of Mathematics, Pi.