What do you do if you're at the seaside, and notice the sea gradually withdrawing - the water getting further and further away, further than for ordinary tides?

Well, sadly everyone knows the answer today. Run like the clappers up the nearest hill or high ground, if you can. As our ancestors might have put it thousands of years ago, the Sea God has breathed in, and you'd better make yourself scarce before he breathes out again.

How are these terrible forces of Nature unleashed?

To understand this we must consider the Earth as a whole. If we zoom out to a view of the Earth we see the thin, fragile layer we call the atmosphere, and beneath it the continents, the islands, and the beautiful blue oceans. The oceans are layers of water about 3 miles thick, except for shallower regions near coasts.

A cutaway, showing Earth's lower and upper mantle in yellow and light blue.
Adapted image, original courtesy of NASA

Underneath the continents and oceans, there is a vast layer of hot rock. Earth scientists call it the mantle (yellow and light blue in the cutaway diagram). It is about 1800 miles thick. From seeing lava coming out of volcanoes you might think that all this hot rock is molten. But we know, from very careful measurement and mathematical analysis of the Earth's vibrations, and from much other evidence, that only a tiny fraction of the mantle is molten. Most of it is solid - well, almost solid.

It's actually more like super-treacle or super-tar. Under huge pressures it can flow just a tiny bit. It does flow, slowly but inexorably, at about the same speed as your fingernails grow. The pressures and the motion are caused mainly by heat generated by radioactivity. The mantle behaves like a gigantic layer of porridge gently heated in a microwave oven.

Scientists used to argue fiercely about whether the mantle flows or not, but today there is no real doubt. We can see the consequences directly from ultra-precise laser measurements; for instance Europe and America are moving apart at fingernail-growth speeds, several centimetres a year. The Atlantic opened up from nothing in about 180 million years.

There is a thin rocky crust - more precisely, the lithosphere - sandwiched between the mantle below and the oceans and continents above. The lithosphere is solid and brittle, like an eggshell. The flow beneath breaks the lithosphere into large, rigid pieces called tectonic plates.

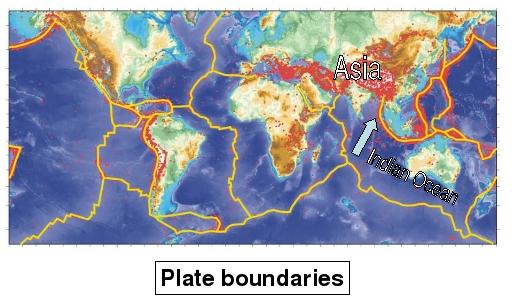
(Image courtesy Prof. James Jackson)

Where the flow beneath is trying to crunch the edges of two plates together, huge stresses gradually build up. Every now and again - just when is impossible to predict - the edges of the plates suddenly slip against each other, shattering some rock and causing an earthquake.

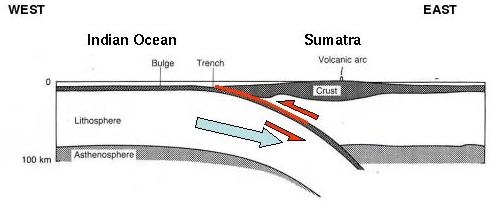
Where the Indo-Australian and Eurasian plates meet near the NW tip of Indonesia
(Image Courtesy Prof. James Jackson)

Some of these earthquakes make parts of the ocean floor rise or fall. If the area rising or falling is much larger than the 3 miles' worth of ocean depth - several tens of miles across, or more - then the most dangerous kind of tsunami is generated. That is what happened on December 26th, 2004, along a strip well over 100 miles wide and 700 miles long. That strip was located near the tip of the large arrow in the plate-boundary map. The strip stretches roughly northwards through the Nicobar and Andaman Islands from Banda Aceh, on the northwest tip of Indonesia. (Find out more about the source of the tsunami, including a movie of the tsunami propagation. You can see a collection of footage of the tsunami from Jordan Golson's blog.)

How does the ocean respond?

To understand the ocean's response we need some wave mathematics.

One reason why most ocean waves are relatively harmless - by comparison with a tsunami - is that their energy spreads rapidly. Drop a stone into a pond and watch the expanding ring of waves. Notice how the number of wavecrests in the ring keeps on increasing. That's called wave dispersion. It means that the energy of the waves is being diluted in two ways: first by the expansion of the whole ring, and second by the widening of the ring to make more and more wavecrests.

If you observe the ring very closely you can see why. The longest waves travel fastest. You can see them at the outer edge of the ring. Wave mathematics tells us that these pond waves travel at speeds proportional to $\surd L$, the square root of the wavelength $L$. (You can see that it must be so from the units of measurement. Speed is measured in metres per second while wavelength, $L$, is measured in metres and gravity, $g$, is measured in metres per second per second, as Galileo is said to have shown by dropping cannon balls from the Tower of Pisa. So the only way to make a speed out of $L$ and $g$ is to multiply them together then take the square root.) This means that a wave twice the length travels about 41\% faster, because $\surd 2 = 1.41...$.

The proportionality to $\surd L$ is accurate as long as the wavelength $L$ is smaller than the depth of water. Then the wavemotion is negligible at the bottom of the pond. The waves don't, so to speak, "feel the bottom", and so $L$ is the only length that can enter the problem.

There's another thing you might have noticed about the ring of pond waves. The whole ring moves at only about half the speed of the individual wavecrests. So crests appear from nowhere at the inner edge of the ring, accelerate slightly as they move toward the outer edge, and disappear when they reach the outer edge. This is perfectly consistent with the measurement units. Wave mathematics shows that individual crests move at speed $\surd(gL/2\pi)$, while the whole ring moves at about $\frac{1}{2}\surd(gL/2\pi)$. Scientists call the first of these the {\it phase speed} and the second the {\it group speed}.

The worst tsunami waves are different. Not only do they have enormous energy, but they are "long waves" in the sense that the wavelength $L$ is many times greater than the ocean depth. All such waves travel at nearly the same speed, so that the energy doesn't spread so much, and individual wavecrests survive over thousands of miles. The phase speed is nearly the same as the group speed, so it makes sense to talk about "the" speed of long waves. Wave mathematics shows that the speed no longer depends on $L$ at all, but is given by $\surd(gD)$, where $D$ is the ocean depth, which remember is about 3 miles or 5000 metres. We can show that the speed of long waves is $\surd(gD)$ from a famous piece of mathematics called Bernoulli's Theorem. (Find out how to use Bernoulli's Theorem to calculate the speed and power of a long tsunami wave.)

Now if you repeat Galileo's experiment you will find that on our planet $g$ is about 10 metres per second per second. So $\surd(gD)$ is about $\surd(10 \times 5000)$ in metres per second, just over 200 metres per second or close to 500 miles per hour, the speed of a jetliner. But remember that although they are fast these waves may have a long way to travel. For example, the great Chilean earthquake of 1960 generated a tsunami that travelled across the Pacific and hit Japan about a day later. So even though earthquakes are unpredictable, warning systems are possible.

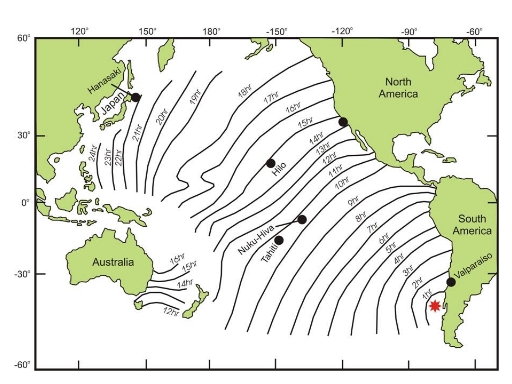
The 1960 trans-Pacific tsunami (Image Courtesy Prof. James Jackson)

The power of a tsunami shows itself when the biggest wavecrests reach shallow water. Suddenly all that energy is squeezed into a much smaller space. Huge walls of water rise up, rushing along at wind speed, often faster than the angriest river. The terrible consequences are all too familiar. The hope is that now, at last, the education, warning systems and infrastructure will be put in place in the Indian Ocean region and in other vulnerable regions, such as the Mediterranean, just as they have long been in place in the Pacific.

Does the Sea God always breathe in first? Only if you are lucky. A tsunami wave can begin either way, with a crest or with a trough. It depends mainly on whether the sea floor nearest you happened to rise or fall. And don't forget that the first crest might not be the biggest.

About this article

Michael McIntyre is a Fellow of the Royal Society and a professor of applied mathematics at the Centre for Mathematical Sciences in the University of Cambridge. This Plus article is appearing concurrently with a shorter version commissioned by the Independent Newspaper's new sixth-form careers magazine TheGuide: MATHEMATICS. We are grateful to Professor James Jackson FRS for supplying several of the images and for advice on plate tectonics.

For further information, a reliable source is the website of the Tsunami Research Program of the Pacific Marine Environmental Laboratory in Seattle, Washington, USA.