
We must know, we will know
This article is a runner-up in the general public category of the Plus new writers award 2006.
"It seems that there was a mathematician who had become a novelist. 'Why did he do that?' people in Göttingen marvelled. 'How can a man who was a mathematician write novels?' 'But that is completely simple,' Hilbert said. 'He did not have enough imagination for mathematics, but he had enough for novels.' "
From Hilbert by Constance Reid.

David Hilbert, 1862 - 1943
Mathematicians are not popularly thought to have brilliant imaginations. Rather unfortunately, and in my opinion wrongly, the mathematician is thought to be a slave to formulae, equations, impenetrable books and dusty blackboards. However I will try to persuade you, by examining the works of the great mathematician David Hilbert, that this stereotype is not typical! Indeed, in many respects, the mathematician must possess an imagination that exceeds that of the writer of the most outrageous fantasy, as Hilbert himself commented.
Throughout his life Hilbert tackled problems in all areas of mathematics — from number theory (the purest of pure maths) to mathematical physics. There's so much that deserves to be written about, but I'll focus only on a few main themes: Hilbert's early work on what is known as invariant theory, his influential approach to geometry, and Gödel's incompleteness theorems.
Maths or theology?
Hilbert was probably one of the greatest mathematicians working in the late 19th and early 20th centuries. He was born in what was then Königsberg, now called Kaliningrad, in 1862, and attended the local university. After finishing his degree and submitting his Habilitation, Hilbert became a lecturer at the University of Königsberg. However, his lectureship was only the first rung on the academic ladder and he received no salary from the university. Instead, Hilbert had to live on the meagre fees which students paid to attend his lectures.

Paul Gordan, 1837 - 1912
Whilst this would have almost certainly been a difficult time financially, Hilbert used it to his intellectual advantage. He took it upon himself to visit no less than 21 renowned mathematicians, including Paul Gordan and Leopold Kronecker. The visits to Gordan and Kronecker in particular were to have important mathematical and philosophical implications. Indeed, after visiting Gordan Hilbert was utterly hooked on a deep problem, and his method of solving it seemed, at that time, strangely supernatural. As Gordan famously complained, "This is not mathematics. This is theology."
Gordan's charge must seem like a strange one today! The fact that Hilbert's resolution ruffled some mathematical feathers may also seem rather odd, given that one of the common (but misguided) views of maths is of a subject where an answer is either right or wrong, with no room for doubt or discussion. However, Hilbert's resolution of Gordan's problem, as it came to be known, was highly creative, imaginative and surprisingly simple compared to the approaches of other mathematicians of the time. The reason it caused controversy was that Hilbert had managed to prove the existence of a mathematical object, and yet his proof said nothing about how to construct it.
The full details of Gordan's problem and the branch of mathematics in which it is found (invariant theory) are beyond the scope of this article. However, I think that it will be worth considering in a little more detail, just to illustrate the beauty and power of Hilbert's result and to give you a taste of some real mathematics.
Loosely, an invariant is some property that remains unchanged after a particular type of action has been applied, such as a transformation. Simple examples of transformations include rotations and reflections.
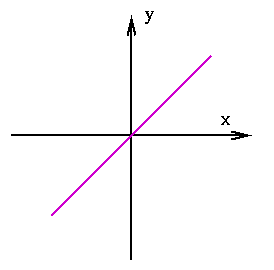
The purple line has the equation x=y.
The above diagram shows the line y=x. A reflection in this line will move a point given by the co-ordinates (x,y) to the point with co-ordinates (y,x). Any point on the line y=x (that is, any point with co-ordinates (x,x)) is mapped to itself. Can you find any lines that are invariant — that is, lines which are mapped to themselves? Clearly, the line y=x is such a line. The lines which are perpendicular to the line y=x are also invariant. How many of these lines are there? There are infinitely many of them, as illustrated below.
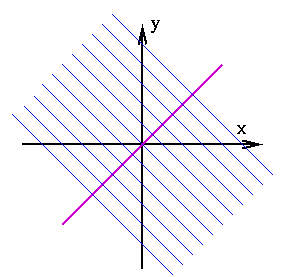
All the blue lines are invariant under reflection in the purple line. In fact, every line which is perpendicular to the purple line is invariant.
Gordan's problem also concerned invariants, though this time of transformations that were more complex than the simple reflection above. Again, there were infinitely many of these invariants, but mathematicians believed that only a finite amount of information was needed to describe them. They imagined the invariants like molecules, each made up of a collection of atoms. It was hoped that a finite collection of atoms would be sufficient to build each and every invariant. The Gordan problem asked if such a finite set of atoms, called a finite basis, could be found.
Gordan was the leading authority on this subject and had even earned the title "king of the invariants" from his earlier success in proving that a finite basis exists in the simplest case. He went about his proof as most mathematicians at the time would have done: he set out to explicitly find a finite collection of candidate invariants and showed that together they indeed formed a basis. This involved enormously complicated calculations and all attempts to extend his approach to more complicated settings failed.
Hilbert's insight was to tackle the problem in a completely different manner. He did not attempt to explicitly construct a basis, or indeed show how you could construct it. Instead, he adopted an indirect approach, avoiding the heavy and difficult computation with which Gordan had previously had success, and in two pages, reached the conclusion that a basis must always exist. It was that simple!
Whilst mathematicians like Kronecker shared Gordan's initial belief that Hilbert's proof was not real mathematics, some mathematicians such as the magnificent Felix Klein, recognised the importance of Hilbert's work. Indeed, even Gordan later realised, as he put it, "That theology also has its merits." (see Hilbert by Constance Reid). Hilbert, whilst remaining firm in his belief of the power of indirect existence proofs, continued to make great progress towards providing the sought-after constructive proof, until it was settled once and for all. Surprisingly, Hilbert then decided to leave the theory of invariants completely.
Axioms or intuition?
Later in his career, after producing some stunning work in number theory, Hilbert shocked his colleagues by working on a subject they never knew he was interested in: geometry. At this time Hilbert was a professor at the University of Göttingen, and his reputation as a first-class mathematician was already established.

Euclid of Alexandria portrayed in a painting by Raphael.
Euclidean geometry is probably the most well-known area of mathematics, and it goes back to the ancient Greeks and earlier. Euclid, who has given his name to the form of geometry with which all school children become familiar, had published his famous Elements in around the third century BC. What was novel about Euclid's approach was his attempt to bring together all of the mathematical knowledge of the day. He did this using definitions and axioms.
Euclid started by defining the basic building blocks of geometry: points, lines, planes, etc. He then set out a series of axioms: self-evident truths which the reader would accept without any proof. An example is the following statement:
For any two distinct points there exists a unique line that passes through both points.
Armed with these definitions and axioms, Euclid set out to prove all of the theorems of geometry without any extra, hidden assumptions. Every step he made in his proofs was to be based purely on his axioms and the rules of logic and not on his geometrical intuition.
However, although Euclid's work was brilliant, mathematicians began to discover that he had not been completely successful in preventing hidden assumptions from creeping in. One of his axioms, called the parallel postulate attracted particular attention. It amounts to the following statement:
Given a straight line and a point not on this line, you can draw only one line through the point that is parallel to the given line.
Mathematicians felt that this axiom was not quite as "self-evident" as all the others and that it needed some proof. However, all attempts at finding such a proof failed. Whilst this in itself did not prove anything, it did suggest that mathematicians might be able to develop some mysterious non-Euclidean geometries that did not adhere to the parallel postulate. And indeed they did. (see Plus article Strange geometries.)
These surprising developments had led some mathematicians, such as Peano, to seek a completely different approach to geometry; one full of formality, abstraction and symbols. Hilbert, however, was to approach geometry in a way more akin to that of Euclid. His style was beautifully clear, which made it arguably much simpler to understand than the approach of Peano and others.
But Hilbert's work was not simply a return to Euclid's method. Whilst it was a radical departure from the work of Peano and others, it was still more formal than Euclid's. Hilbert maintained that the words point, line and plane gained their meaning not from their definitions, but from their relation to the axioms. Whilst Hilbert used the same terminology as Euclid, he claimed that he could just as well have used other words such as "chairs", "tables" and "beer mats" instead of points, lines and planes. In his view, the true essence of a geometrical system lay not in its objects, whatever they may be, but in the axioms that govern and define their interaction — if based on a coherent set of axioms, a geometry of tables, chairs and beermats was just as viable as one of points, lines and planes. Many of Hilbert's contemporaries were not happy with this approach, notably the eminent mathematician and philosopher Gottlob Frege, who published rather bitter criticisms of his work.
Maths or philosophy?

Hilbert's grave in Göttingen. The gravestone carries the quote 'We must know, we will know' in German. Image courtesy Suitbert Ertel.
Hilbert's work on geometry went beyond the mathematical. It took him into the philosophy of mathematical proof. His axiomatic approach led him to ask what kind of geometry a set of axioms was capable of creating and what kind of criteria a set of axioms should satisfy in order to give rise to a meaningful geometry.
He came up with three essential concepts. First, he maintained that the axioms should be consistent. This means that they cannot give rise to contradictions: they don't allow you to prove a geometrical result and also its negation. Second, he thought that the axioms should be complete, meaning that using them you could prove all geometrical theorems. Finally, he claimed that the axioms must be independent, meaning that they do not carry excess baggage: if you removed anyone of them, the resulting set of axioms would be incomplete.
These criteria of consistency, completeness and independence were to be of great importance. They lead to the development of what is today known as metamathematics, which means, "beyond mathematics". It's the science, or more accurately the philosophy, of understanding how mathematics should be done and how far it can reach. Hilbert had strong opinions on these matters: he believed that every mathematical problem had a solution, and his famous words "We must know, we will know" are emblazoned on his grave stone in Göttingen.
However, a young logician named Kurt Gödel was to shatter some of Hilbert's hopes for mathematics. Gödel was interested in the completeness and consistency of mathematical systems that are defined, like Hilbert's geometry, by a set of axioms together with logical rules that tell you how to manipulate mathematical expressions. But rather than looking at axioms that generate geometry, he looked at axioms that can generate the whole numbers and their arithmetic (see Plus article Gödel and the limits of logic). In his first ingenious proof, Gödel demonstrated that any such system is essentially incomplete. This meant that no matter which, or how many, axioms you choose to define the whole numbers, there always is some true statement about the whole numbers that you can never prove. So maths doesn't have all the answers after all!
But even if we can't prove everything about the whole numbers using Hilbert's axiomatic approach, can we at least make sure that a given system doesn't give rise to contradictions, in other words that it is consistent? Unfortunately, Gödel also proved that while this is theoretically possible, it is incredibly unlikely. Indeed, no-one today has any idea of where to start looking for such a proof, or even what a proof of this kind may look like.
Although Gödel's results devastated some of Hilbert's beliefs about the nature of mathematics, they do not mean that we need to despair of maths. Far from it! As my teacher told me when I felt disappointed after learning of these results, it makes it all the more exciting! I believe that Hilbert's words "We must know, we will know" should spur us all on. Maths is full of mystery, full of beauty and I'm sure it has many surprises left in store for us. All we have to do is to follow Hilbert and use our imaginations.
About the author

In her spare time, she enjoys writing poetry, walking and reading about the history of mathematics and science.