What mathematicians get up to
After 5,000 years, the game of Nine Men's Morris has succumbed to the power of modern computing. William Hartston looks at other recent mathematical discoveries in the world of games.
Ancient games from Iceland, India and England
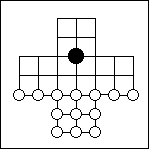 hala-tafl (mentioned in the 14th-century Grettis Saga); White's 13 geese try to stifle the black fox to death before it "eats" them by jumping over them. |
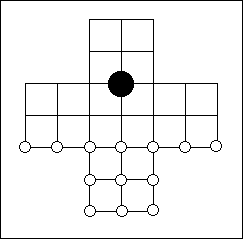
 Pulijudam (the tiger game): three tigers fight against 15 lambs on a 23-square board. The tigers can jump over (and "eat") the lambs; the lambs must try to crowd the tigers to prevent them from moving. |

Nine Men's Morris.
"The fold stands empty in the drowned field
And the crows are fatted with the murrain flock;
The Nine Men's Morris is filled up with mud,
And the quaint mazes in the wanton green,
For lack of tread are indistinguishable."-- 'A Midsummer Night's Dream' Act 2, scene 1.
"Nine Men's Morris is a draw."
-- Ralph Gasser, Games of No Chance, 1996.
As computers have become faster and faster, their capacity has grown to analyse traditional games to extinction. While chess and Go still contain vastly more possibilities than any computer can hope to analyse exhaustively, other games, in which the space of possible positions is less huge, can now be played perfectly by machine.
We are not talking here simply about machines playing better than humans. When mathematicians play games they will be satisfied by nothing less than perfection, and a recently published book shows how perfection has been achieved in a number of games, and how close to or far away from it machines still are in others.
Games of No Chance, edited by Richard J Nowakowski (Cambridge University Press, £40), is a series of articles based on the seminars given at a workshop in 1994 on the branch of mathematics that is known as combinatorial game theory.
Mathematicians are quite clear about what comprises a game:
- There are two players;
- They move alternately;
- There are no dice or other chance devices.
- They both have perfect information about all the elements of the game;
- The game cannot go on for ever;
- There are no draws;
- The last player to move wins.
So that cuts out bridge (by rule 4) and chess (by rule 6) and backgammon (by rule 3) for a start, but just to show how magnanimous they are towards our less rigorous games, the workshop participants spend a good deal of their time looking into traditional, faulty games, as well as those that satisfy the above definition.
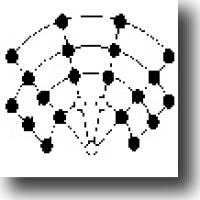
One such impure game is Nine Men's Morris, which has been around since 1400BC. Each player starts with nine men, which are placed in turn on a board of 24 squares (see illustration). When all 18 men have been placed on the board, play continues by moving them a square at a time. The object, both in the initial phase and the later play, is to form a straight (not diagonal) row of three men. Each time this is accomplished, on of the opponent's men may be removed from the board.
Now here's the abstract of Ralph Glasser's paper from the book:
"We describe the combination of two search methods used to solve Nine Men's Morris. An improved analysis algorithm computes endgame databases comprising about 10 billion states. An 18-ply alpha-beta search then used these databases to prove that the value of the initial position is a draw. Nine Men's Morris is the first non-trivial game to be soled that does not seem to benefit from knowledge-based methods."
In other words, they got the machine to work out and tabulate 10 billion positions that they knew were a win for one side or the other, then worked forward 18 moves from the beginning of the game until their opening analysis met their endgame analysis. Result, a recipe for perfect play that guarantees either side freedom from defeat.
As you may have guessed by now, some of the mathematics is formidable, and some of the numbers involved are enormous. For example, another game that has succumbed to computer power is Pentominoes. You start with an empty chessboard and the 12 regular pentominoes - the distinct shapes that can be formed from five connected squares. At each turn a player selects a pentomino and places it in an empty space on the board, not overlapping any previously placed piece. Each pentomino may be used only once. The first player who cannot move, loses.
Hilarie Korman's paper "Pentominoes: A First Player Win" proves precisely that - and it took a Sun IPC Sparcstation five days of solid computing to do it. As she says, however, the program did have to look at 22 billion board positions to reach its conclusion.
As for the game of draughts, you may be interested to know that the total number of possible positions in the game is 500,995,484,682,338,672,639, and even that may soon not be beyond the largest computers.
None of this, however, is likely to stop determined humans from playing all the above-mentioned games. So turn your computers' faces to the wall and have a go at two particularly ancient ones, illustrated above.
Hala-tafl
Hala-tafl (the fox game) is played on the board above. Both the fox (the black piece) and geese (white ones) can move one square along a line to a vacant point. The fox may also jump over a goose (as in draughts) to land on the point on the other side - and if it does so, the goose is "eaten" and removed from the board. The fox can eat more than one goose in a single move, by a series of connected leaps. The geese cannot jump over the fox, but they can win by crowding him to death,. by depriving him of moves. This game has been known for a long time to be a win for the geese, but it may be an improvement to increase the number of geese to 17 and not let them move backward.

Pulijudam (the tiger game)
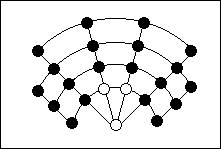
The Indian game of Lambs and Tigers (above) is similar: tigers jump and eat, lambs cannot capture, but you start with an empty board on which the three tigers and 15 lambs must be placed in the early moves.
The tigers must be put on the three white squares; none of the lambs may move until all 15 have been placed on the board. Off you go - and remember, no computing.