
Will machine learning replace mathematicians?
This article is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below and see other articles based on the talk here.
In the previous articles we have looked at machine learning, a bit of its history, and its applications. Now we ask the question of whether machine learning will lead to a robot that can do mathematics. A naïve answer is "yes of course". Indeed according to a well known celebrity (who I won't identify by name) now we have computers we don't need university maths departments anymore.

As of yet, computers are unable to do deep mathematics.
It is certainly true that computers can be trained to do mathematical calculations very fast. Indeed my (day) job as a numerical analyst is to do exactly that. Furthermore the Todai robot beat 99.1% of the candidates in the mathematics part of the Japanese university entrance exam (although it only beat 64% of the physics candidates). However, in all of these cases the computer is basically doing arithmetical operations, pre-programmed by a human operator. None of this shows that a computer could learn to do deep mathematics, in the sense of identifying and proving results such as Fermat's last theorem. Nor indeed are robots like the Todai one displaying mathematical reasoning.
Whether or not machines can reason mathematically is an important question and goes back (at least) to the great mathematician David Hilbert. At the start of the 20th century Hilbert started a program to write all mathematical statements in a precise formal language, only allowing those statements to be manipulated according to well-defined rules. He also stipulated that all true mathematical statements should be provable in the formalism.
Hilbert's goal, if achieved, would essentially reduce mathematical theorems and proofs to exercises in arithmetic. I see this as entirely consistent with an expectation that a machine learning approach would be appropriate for mathematics. Unfortunately for this approach in 1931 Kurt Gödel, in his incompleteness theorem, showed that Hilbert's program was unattainable for many important areas of mathematics (see this article to find out more).
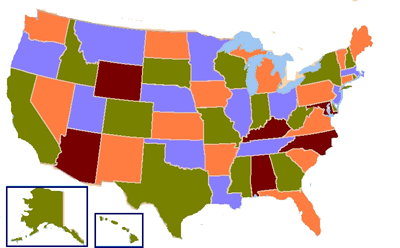
The US in four colours. Image: Wikipedia.
This doesn't of course mean that computers cannot be incredibly helpful in mathematical discovery. An excellent example of this was the proof of the celebrated four colour theorem, which was very much a combined effort of mathematicians and computers working together (see this article to find out more). Indeed computers are opening up whole areas of experimental mathematics, aiding mathematician in making new discoveries.
Having said all of this, there is (as far as I am aware) no machine learning program which has made a dent in the notoriously hard problem of factorising integers. (The difficulty of doing this is a key element of the security of modern cryptography, find out more here.) Much the same can be said of the (equally notorious) travelling salesman problem. I am personally waiting to see if machine learning can ever replace modern algorithms for the five-day weather forecast.
Mathematics is a creative activity and perhaps it is a lack of creativity that stops machine learning algorithms from doing deep mathematics. More generally we can ask whether a machine learning algorithm will ever be able to solve a problem that everyone would consider to require creativity. In analogy to the Turing test I suggest a test in which we play a computer all of the works of the great composers. This would be considered its training set. We would then as a task ask it to compose a completely novel symphony. If that could then be played to an expert musician and found indistinguishable in imagination and invention from that created by a human being, then algorithm could be considered creative. I wonder if I will see that day?
About this article
This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.