Winding numbers: Topography and topology II

by Ian Short

Submitted by mf344 on March 23, 2011
in

This is the second in a series of two articles in which we look at topology using topographical features of maps. You may wish to read the first article on dividing walls, although the two articles are largely independent.

The Jordan Curve Theorem

A hermit hires some builders to construct a wall around his house. The wall they construct is shown in figure 1. Does the wall actually surround the house?

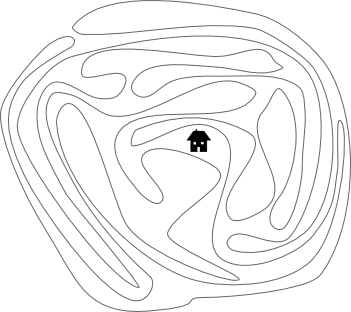
figure 1

Figure 1: A house surrounded by a wall?

A Jordan curve in a plane is a continuous loop that doesn't intersect itself. The Jordan curve theorem states that each Jordan curve divides the plane into an inside region and an outside region. This is intuitively obvious, but difficult to prove on a more formal level (which we won't go into). But how can we establish whether the house lies inside or outside the Jordan curve?

First notice that each Jordan curve can be deformed, in a continuous fashion, to a circle, as indicated in figure 2.

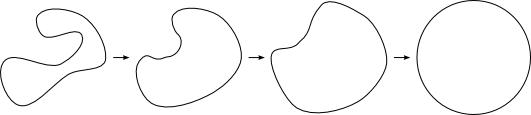
figure 2

Figure 2: A continuous deformation of a Jordan curve to a circle.

Think of the Jordan curve as a loop of string, which you can deform (without it crossing itself at any stage) to a circle shape. If the builders had built a circular wall, we wouldn't have a problem because it is clear what is the inside and outside of a circle. Now imagine walking from the inside of a circular wall to the outside, along some arbitrary path, as shown in figure 3. How many times do you climb over the wall?

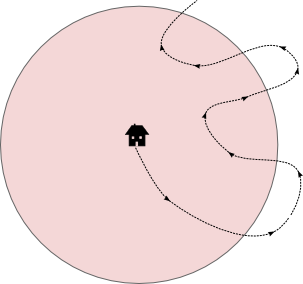
figure 3

Figure 3: A path from the inside to the outside.

The answer is you climb over the wall an odd number of times, because each time you climb the wall you either move from inside to outside, or outside to inside. The same should be true of our original complicated wall! So let's take any path from the house to the outside, and count how many times we climb the wall (see Figure 4).

figure 4

Figure 4: A path from the house to the outside.

The path crosses the wall four times. Four is not odd so the house does not lie inside the wall! Of course, I could have just clicked 'fill' when creating figure 1 and saved us having to think.

figure 5

Figure 5: The original Jordan curve, with shaded interior.

Self-intersecting loops

The loops in the previous section each had an inside and an outside. What about the loop in figure 6; does the house lie inside or outside the loop?

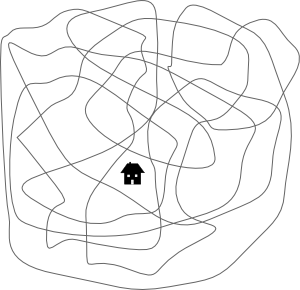
figure 6

Figure 6: A self-intersecting loop.

Unlike the Jordan curves in the previous section, the loop in figure 6 intersects itself, and the meanings of inside and outside are no longer clear. We leave this issue for the moment (until the next section) and move on to a well-known, related problem.

In figure 7 there is a picture of the hermit's house, hung using a loop of string over two nails. If either nail is removed, the picture will still hang from the other nail (although it will be skewed). Is it possible, using an alternative loop, to hang the picture from the two nails in such a way that if either nail is removed, the picture falls?

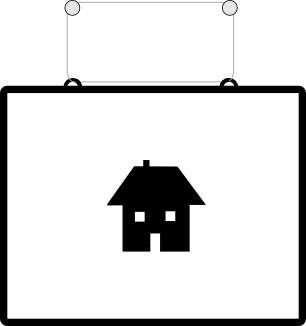
figure 7

Figure 7: The hanging picture problem.

Winding numbers

Now let's try to solve these two problems. Jordan curves have an inside and an outside. A self-intersecting loop partitions the plane into more than two regions, and it is unclear which of these regions should be deemed to lie inside the loop, and which lie outside. We address this issue mathematically, using winding numbers.

Suppose there are three islands, shown in figure 8, on each of which is a lighthouse. The lighthouses are labelled A, B, and C. A drunken sailor steers a complicated loop round the islands (shown by a directed line in figure 8). Fearing a collision, each lighthouse focuses its beam on the sailor's ship for the entire loop. How many times, in total, does each lighthouse rotate whilst the ship traverses the loop once? Lighthouse A rotates twice anticlockwise. Lighthouse B rotates once clockwise. Lighthouse C rotates in total zero times anticlockwise. The winding number of the loop about a lighthouse is the total number of rotations of the lighthouse, where anticlockwise rotations are considered to be positive and clockwise rotations are considered to be negative. So the winding number of this loop about A is 2, the winding number about B is -1, and the winding number about C is 0.

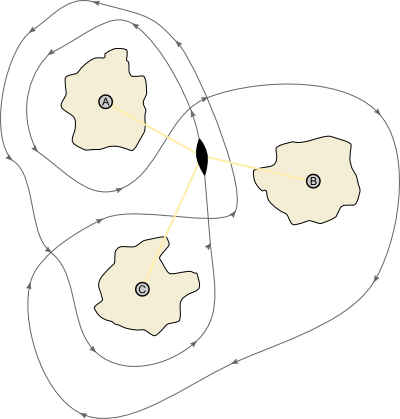
figure 8

Figure 8: The route of the drunken sailor.

We don't need sailors and lighthouses to define winding numbers; we just need a directed loop (a loop with arrows) and a point (representing a lighthouse). Given such a loop $\alpha ,$, and such a point $p,$ we denote the winding number of $\alpha $ about $p$ by $w(\alpha ,p).$ So, for figure 8, $w(\alpha ,A)=2,$ $w(\alpha ,B)=-1,$ and $w(\alpha ,C)=0.$ In figure 9 we have removed the ship and the islands from figure 8, and labelled regions according to the winding numbers of points in that region.

figure 9

Figure 9: A directed loop with winding numbers labelled.

Why is the winding number constant within each region separated off by the loop? Here is an informal explanation. Consider two points $p$ and $q$ inside the same region. Let $p_1$ be another point in the region, very close to $p$ and not too close to the loop. Two lighthouses positioned at $p$ and $p_1$ will face in roughly the same direction as a ship sails round the loop. Therefore the winding numbers at $p$ and $p_1$ are equal. We can apply the same reasoning to the pair of points $p_1$ and $p_2,$ where $p_2$ is chosen to be close to $p_1,$ and not too close to the loop. Continuing in this fashion we can create a sequence of points $p, p_1, p_2, ..., p_ n, q,$ where each pair $p_ i$ and $p_{i+1}$ are close, $p_ n$ and $q$ are close, and no point is too close to the loop. The winding numbers of all these points are the same, and hence the winding numbers about $p$ and $q$ are equal.

Notice that the infinite region surrounding a loop always has winding number 0, but there may be other regions of winding number 0 within the loop (as is the case in figure 9).

Deforming loops

In figure 2 we deformed a Jordan curve, in a continuous fashion, to a circle, without at any stage in the deformation process creating an intersection. We continue our study of continuous deformations of loops, and this time we allow intersections. We are interested in continuous deformations that do not cross a given point. See figure 10.

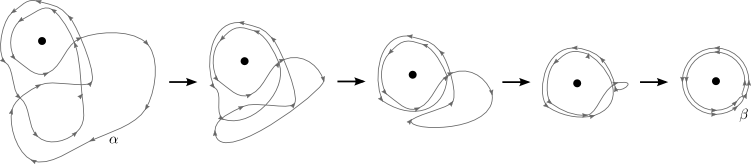
figure 10

Figure 10: Continuous deformation of ⍺ to β without intersecting a point.

Let $p$ be the black point shown in each loop of figure 10. We continuously deform the loop $\alpha $ to the loop $\beta $ without ever crossing $p.$ Notice that the winding number of $\alpha $ about $p$ is equal to the winding number of $\beta $ about $p.$ In fact, more generally the following is true: a loop $\alpha $ can be continuously deformed to a loop $\beta $ without ever crossing a point $p$ if and only if the winding number of $\alpha $ about $p$ is equal to the winding number of $\beta $ about $p.$ This is a special case of Hopf’s degree theorem, which is a stronger result that holds in all dimensions, not just the plane. We will not prove this theorem here, but we use it in our final section when we return to the picture problem.

Calculating winding numbers

We asked of figure 6 whether the house lies inside or outside the loop. Once we have given the loop a direction, a more mature question is to ask for the winding number of the loop about the house. See figure 11, where the house is now replaced by a point.

figure 11

Figure 11: What is the winding number of the loop about the point?

There are two good methods for solving problems of this type. The first is to use the special case of Hopf's degree theorem described in the previous section. We deform the loop, without crossing our point, to a simpler loop for which we can easily calculate the winding number. But there is also a better method. Consider two points, or lighthouses, $A$ and $B$ which are very close together, but on either side of a loop $\alpha $. As the ship traverses $\alpha $, the lighthouses will point in approximately the same direction except when the ship sails between them. When the ship sails between them, one lighthouse will rotate 180° clockwise, and the other will rotate 180° anticlockwise. 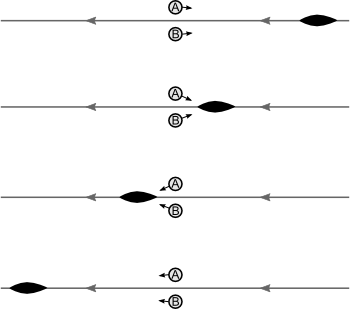See figure 12. Thus, in total, the winding number of $\alpha $ about $A$ will differ by 1 from the winding number of $\alpha $ about B.
figure 12

Figure 12: What is the winding number of the loop about the point?

Let us use this observation to calculate the winding number of the loop in figure 11 about the given point $p.$ Construct a path from a point $q$ in the infinite region outside the loop to $p.$ The winding number about $q$ is 0. Using the observation of figure 12 we can calculate the winding number in one region after another, from $q$ to $p,$ being careful each time whether we should add or subtract one (depending on the direction of the arrows as we cross the loop). See figure 13; the winding number about $p$ is 2.
figure 13

Figure 13: Winding numbers of adjacent regions differ by one.

Solution of the picture problem

We return to the picture problem described above. First, thinking topologically, we remove the picture as it is merely a distraction, and has no real bearing on the problem. We are left with two nails and a loop of string. Let us represent the nails by points $A$ and $B,$ and let $\alpha $ denote the loop of string. We define a null loop to be a simple circular loop whose inside contains neither $A$ nor $B$ (see figure 14). This means that a null loop could not be used to hold up our picture. Notice that the winding number of the null loop about $A$ and $B$ is zero.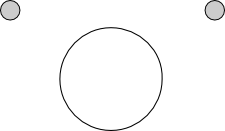
figure 14

Figure 14: A null loop.

We must show that if $A$ is removed then $\alpha $ can be continuously deformed, without crossing $B,$ to the null loop (so the picture falls). By Hopf's degree theorem, this is possible if and only if $w(\alpha ,B)=0.$ Likewise, we require that $w(\alpha ,A)=0.$ So, we seek a loop whose winding number about $A$ and $B$ is zero. The null loop satisfies this, but any loop that can be continuously deformed, without crossing either $A$ or $B,$ to the null loop wouldn't hold up the picture in the first place. So we must ignore such loops. 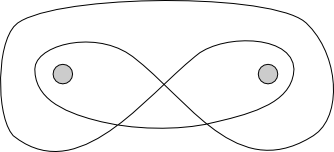A first solution to the picture problem is shown in figure 15. It cannot be continuously deformed to the null loop without crossing $A$ or $B,$ and, once the loop is given a direction, the winding number about $A$ and $B$ is zero.
figure 15

Figure 15: A simple solution.

Using our winding number calculating skills we can come up with more complicated solutions than that though; see for example figure 16.

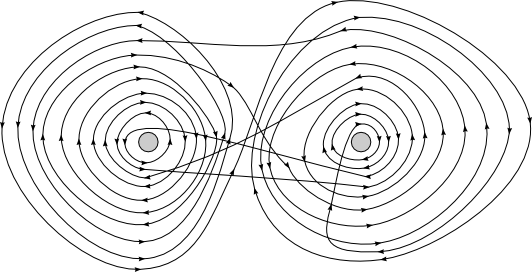
figure 16

Figure 16: A complicated solution.

Can you describe all possible solutions to the picture problem? You should consider two loops to be equivalent if one can be continuously deformed to the other without crossing $A$ or $B.$ For a deeper understanding of the problem, try researching the fundamental group. This will lead you into a branch of topology known as algebraic topology, which is concerned with the interaction between algebra and topology.

About the author

Ian Short

Ian Short is a lecturer in mathematics at the Open University. His mathematical interests include complex analysis, continued fractions, dynamical systems, hyperbolic geometry, and uncertainty.

Comments

Interesting article

Submitted by Anonymous on April 10, 2011.

Very nice article ... I enjoyed reading it.

Winding Numbers and Topology

Submitted by Anonymous on April 8, 2011.

Thanks so much. These are the types of explorations that brings math alive for students in Math Club.

Topology

Submitted by Anonymous on March 29, 2011.

Nice! Love it! Thanks! =))