A Menger sponge. Image: Niabot.

Would you like to help build the world's largest distributed fractal? Then head for the Centre for Mathematical Sciences in Cambridge on October 25th. You can help to build a model of a Menger sponge — that's a fractal which has so many holes it contains no volume at all, but is so crinkly it has infinite surface area.

The effort is part of the MegaMenger project, which aims to build a distributed global fractal in multiple sites worldwide, made from business cards. The model that will be built in Cambridge will be made out of 8,000 small cubes using 48,000 business cards. It will weigh over 90kg and be 1.5 metres tall, wide and deep. Drop in at any point during the day (11am - 3pm) to join in and to experience a wide range of other hands-on mathematical activities for all ages from 5 to 18 (find out more here).

What's a fractal?

Fractals are objects that exhibit complex structure at every scale. No matter how closely you zoom in on a fractal, its complexity doesn't diminish and you often see the same structures appearing again and again. A famous example, a little easier to describe than the Menger sponge, is the Sierpinski carpet. Start with a square and divide it into nine smaller squares. Remove the middle one of these nine squares. Now do the same for each of the eight remaining squares (dividing them into nine and removing the middle one) and repeat, ad infinitum. The shape you get in the end is riddled with holes. No matter how closely you zoom into it you won't find a single little patch that doesn't have any holes in it.

The first few steps towards creating a Sierpinski carpet. for the full carpet you need to repeat the process an infinite number of times. Image: Arbol01.

So how much area does Sierpinski's carpet occupy? The answer is zero. It has so many holes, there just isn't any area left. This means that it's fundamentally different from two-dimensional shapes, like squares or discs. If you take away the inside of a square, you are left with its sides, which are one-dimensional lines. So by analogy, perhaps we can think of Sierpinski's carpet as a one-dimensional shape too? The answer is again no. If you walked along the carpet's outline, you would find that it is infinitely long while confined to a finite area. Sierpinski's carpet is way more complex than an ordinary one-dimensional curve.

This is what defines fractals: they live in a strange world in between dimensions. Mathematicians have had to come up with new definitions of the concept of dimension to sort out their place in the dimensional hierarchy. According to one of those definitions, Sierpinski's carpet has a dimension of around 1.9. Having a fractional dimension, one that's not a whole number, is what characterises fractals and what gave them their name.

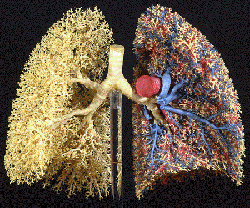
A model of a set of lungs. The intricate branching guarantees maximal exposure to oxygen molecules. Image courtesy Professor Ewald R Weibel, Institute of Anatomy, University of Berne.

Fractals may seem like mathematical oddities but they are not. Many real-life shapes exhibit a self-similar complexity akin to those of fractals. A coastline looks just as crinkly whether you look at it on a satellite image or from a cliff overlooking a beach. Stock prices show a similar kind of variation over a period of a year as they do over a week. And our lungs exhibit an intricate branching structure similar to that of some fractals. That's no accident: lungs need to fit into the confined space of our chests (they need to have a small volume) but have as much surface area as possible in order to diffuse a maximal amount of oxygen through their surface. Being crinkly like a fractal makes that possible.

The mega Menger sponge

The Menger sponge is also a fractal. It's similar to the Sierpinski carpet, only that instead of starting with a square and removing little squares you start with a cube and remove little cubes (see here for instructions). It has zero volume but its surface area is infinite. Its fractal dimension is around 2.7: it's more than two-dimensional but not quite three-dimensional.

Building a true Menger sponge is impossible, as it's infinitely complex, but the one we will build in Cambridge will be a good approximation of one. It will go to the third level of the iterative construction process. And because we don't want to do any drilling or tunnelling, rather than starting with one large cube, we will build it up from many little cubes. If you're asking yourself how on Earth this is possible using business cards, then head to Cambridge or follow the MegaMenger project online.

You can read more about fractals on Plus.