
Cellular automata
This article is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below and see other articles based on the talk here.
Cellular automata are widely used in physics, chemistry and biology to model many types of natural phenomena: from the patterns on animal coats to bacterial infections. They also turn out to have pleasing applications in recreational mathematics including knitting. Cellular automata can display a wide variety of the astonishing dynamical behaviour we described in a previous article.
The concept of the cellular automata was developed in the 1940s by Stanislaw Ulam and John von Neumann while they were at the Los Alamos National Laboratory. In the 1970s Conway's Game of Life, a two-dimensional cellular automaton, led to an interest in them which expanded beyond academia and into recreational maths after it was popularised in Scientific American. In the 1980s, Stephen Wolfram engaged in a systematic study of one-dimensional cellular automata. Wolfram published A new kind of science in 2002, claiming that cellular automata have applications in many fields of science.
One dimension
A one-dimensional cellular automaton consists of a row of cells, each cell containing a number. At regular time intervals the number in each cell changes according a given rule (which usually depends on the numbers in the neighbouring cells). For example, you could start with a row of zeros and ones such as
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
We consider this the first generation row. Now create a second generation row according to this simple rule:
- Keep the first digit as 1 and the last digit as 0
- Replace the number in all other cells with
- a 0 if the numbers in the two cells on either side are the same
- a 1 otherwise
The second generation cell is
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
You can create third, forth, fifth, etc generation rows by applying the rule again and again. The following table shows the first five generations:
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
(For those familiar with the terminology, the new number in a cell is the XOR of its neighbours in the previous generation.)
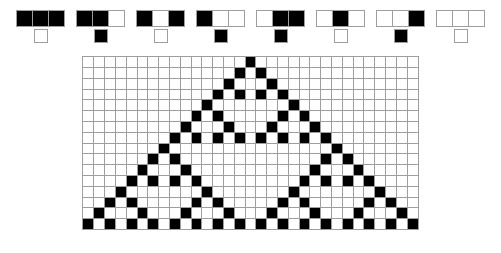
It is clear from this example that even a simple rule can lead to a complex pattern. We can visualise the pattern better if we paint each cell containing a 0 white and each cell containing a 1 black. If, unlike in the example above, the first row contains a single black cell (a single 1) right in the middle, the first 15 generations of the rule above look like this:
Rule 90. The top row shows how the colour of each cell is changed depending on its colour and the colour of its neighbours in the previous generation. We created this picture using Representing Elementary Cellular Automaton Rules by Daniel de Souza Carvalho from the Wolfram Demonstrations Project.
If we continue to apply the rule the following pattern emerges. It is exactly what you get if you colour the odd values of Pascal's triangle black and the even values white. It has a very rich structure; in fact it's a fractal called the Sierpinski gasket, which has the same structure repeated at smaller and smaller scales.

Rule 90 with 256 generations. Image: eouw0o83hf, CC BY-SA 4.0.
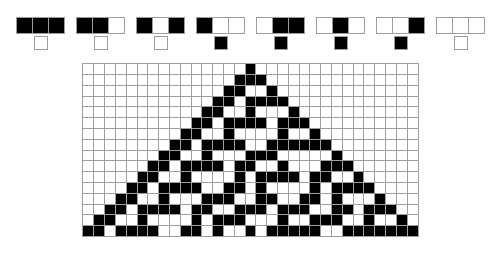
Wolfram gave a series of different rules for one-dimensional CAs many of which generated remarkably complicated patterns. The above is Wolfram's rule 90. Below are the first 15 generations of rule 30:
Rule 30. The top row shows how the colour of each cell is changed depending on its colour and the colour of its neighbours in the previous generation. We created this picture using Representing Elementary Cellular Automaton Rules by Daniel de Souza Carvalho from the Wolfram Demonstrations Project.
If we continue to apply rule 30 then we get the following pattern, which is remarkable for its complex structure. Note that on the left it appears to be quite regular, but this regularity vanishes as we move to the right, where we see a disordered and chaotic pattern.

Rule 30 with 256 generations.
Wolfram has classified one-dimensional cellular automata: he described automata in which patterns generally stabilise into homogeneity, automata in which patterns evolve into oscillating structures, automata in which patterns evolve in a seemingly chaotic fashion, and automata in which patterns become extremely complex and may last for a long time, with stable local structures.
Remarkably, we see very similar patterns in nature, for example on shells. Here is an example of a conus textile shell with a very similar pattern to that of Wolfram's rule 30. Presumably, the growth of the pattern is driven by a similar rule.

A conus textile shell. Photo: Richard Ling, CC BY-SA 3.0.
Two dimensions
We can extend the above idea to two dimensions: start with a two-dimensional grid of cells containing numbers as a first generation and then replace the numbers in the cells according to some given rules. Two-dimensional cellular automata go back to Von Neumann who worked with them in the 1940s, and are often used to model disease and infection processes.
A famous example of a two-dimensional cellular automaton is John Conway's Game of Life, which is supposed to produce patterns that resemble living organisms. The Game of Life is played on an infinite two-dimensional grid of square cells. As above, we can replace numbers by colours. A cell that is green is considered to be alive and a cell that is grey is considered to be dead. Every cell interacts with its eight neighbours which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
- Any live cell with fewer than two live neighbours dies (as if caused by underpopulation).
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies (as if by overpopulation).
- Any dead cell with exactly three live neighbours becomes a live cell (as if by reproduction).
The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules, simultaneously, to every cell in the seed. As with the one-dimensional cellular automata, the rules continue to be applied repeatedly to create further generations. Depending on the seed, very exotic patterns can emerge.
You can explore the Game of Life in the interactivity below, created by our amazing colleague Oscar Gillespie. It starts off with a random pattern of live cells. If you would instead like to choose your own starting arrangement of live cells, click Clear the grid and then click on the individual cells you would like to be live. To run just a single step of the Game of Life, click on Run a generation. To run through many steps, click Run. And to start again, click Stop and then Reset.
Here are some examples of interesting patterns that emerge. The cloverleaf is an oscillating pattern which repeats periodically. Press play in the video below to watch the pattern evolve. (We have created these movies using Edwin Martin's online version of the Game of Life.)
For an exercise, try and find a pattern that remains completely fixed.
The shape of the hammerhead spaceship also repeats periodically in time, but moves along the grid, as if it had somewhere to go.
A famous pattern is the glider which, as the name suggests, glides across the grid.
The Gosper glider gun gun produces an unending stream of gliders, as if by design.
Claims have been made that the Game of Life mimics real life processes (and even that the whole of humanity might just be the agents of some cellular automaton being played by extra terrestrial beings!). While this is theoretically possible it is extremely far-fetched. Indeed, John Conway designed the game of life by looking for the simplest possible set of rules that would lead to complex, evolving, patterns. You can find out more about the Game of Life in our interview with Conway.
However, it is certainly true that two (and indeed three) dimensional cellular automata are used very effectively to model the action of bacteria, disease and infection. In particular we can model biological cells by the cells in the grid, and also model bacteria by other cells. Just as in the Game of Life we can look at biological cells and bacteria as being alive or dead. Such models were the original motivation for the work of Von Neumann and are used predictively to study many types of disease propagation.
Cellular automata illustrate how ordered and seemingly purposeful behaviour can emerge from mindless entities — the cells — interacting according to simple rules. And as we already mentioned at the start of this article, they can be used to simulate many system that arise in nature. In the next article we will examine types of system that allow the individual entities to move around: they are called agent based models.
About the author
This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.