
Fractal music
Fractals are a treat for your eyes, but what about your ears? Dmitry Kormann, a composer/keyboardist from São Paulo, Brazil, explains how he brings fractal-like patterns to the very structure of his music, to obtain beautiful results.
Listen to the following five pieces composed using Kormann's fractal system.
- Coral reef symphony: part 1
- Coral reef symphony: part 2
- Coral reef symphony: part 3
- Wind and metal
- Anemonae
All tracks © Dmitry Kormann (MCPS/PRS Alliance member).
Some simple fractals
Fractals are geometric constructs that exhibit similar or identical characteristics at every level of magnitude. They provide new tools for geometers to describe objects of extreme intricacy, such as clouds, ferns, snowflakes, mountain ranges, stock-market fluctuations, the human circulatory and nervous system, etc. They have been used in art for a long time, way before the term fractal was even coined in the 1970s.
Some of the most popular examples are:
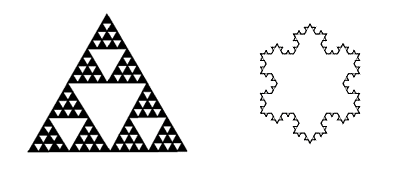
The Sierpinski triangle (left) and the Von Koch snowflake (right, image from Wikipedia).

The Mandelbrot set.
Some fractals, for example the Sierpinski triangle and the Koch snowflake, can be generated by a reasonably straightforward process: a basic form is used as a starting point, some alteration is applied, and the resulting object is transformed by the same alteration, ad infinitum:

The Sierpinski triangle is created by removing a smaller triangle from the center of the larger black one, and then repeating this porcess for every new black triangle.
Of course, some fractals, such as the Mandelbrot set above, involve more complex mathematics which is beyond the purpose of this explanation, but I think the simple examples above illustrate the point beautifully. (Click here for more on the Mandelbrot set.)
As far as the development of my fractal music system is concerned, the whole thing came about almost by chance. Since my teens I was already having lots of fun with aleatoric music generators, which incorporate elements of chance. Sometimes using nothing more than dice and a chart, sometimes with my own generator written on the Brazilian equivalent of the ZX Sinclair. Later I started rendering graphic fractals as sounds with software converters such as Coagula and Metasynth. Then, as a more mature composer, I began to wonder about the possibilities of applying fractal geometry to form and structure, instead of pitch, dynamics, timbre and rhythm. Preferably a system that I could incorporate into my personal style, as opposed to something I worked on in parallel.
Loops within loops
Anyway, I just happened to be studying the piano version of Stravinsky's Rite of Spring. I was quite taken by the way in which Stravinsky managed to maintain interest and ascertain forward momentum while using harmonically static material such as ostinatos (these are loops — motifs which are persistently repeated) by alternating them with other ostinatos, and nearly always changing their length. This can be clearly observed in the beginning of the Games Of The Rival Tribes:

I was also particularly captivated by the way he created forward momentum by making motifs come out from inside one another, so to speak. As opposed to minimalist-styled transformations, where textures just fade in and out of each other, Stravinsky alternates progressively larger instances of a new motif with progressively smaller instances of an ongoing one. This is best illustrated by what happens from fig.84, in the Mystic Circle of the Adolescents.

We first hear what we'll call motif A for three bars. Then a motif B pops in for a single isolated bar surrounded by rests and a special motif which we'll call X, until motif A comes back slightly altered, and only for two bars this time. Motif B comes back and stays for longer, this time for four bars. On the fourth bar, we hear a two-bar hint of motif C overlapping with motif B. Then motif B returns one last time for only two bars, before motif C settles in for ten bars.
(See my website for a further example of a similar structures within The rites of spring.)
Self-similar structures
Meanwhile, I had just come across an analysis of John Cage's percussion sextet First Construction (In Metal). I was fascinated by his multi-scalar, self-similar (fractal-ish?) textures. Micro-macrocosmic relationships have featured strongly in most of his percussion music for almost 20 years. This is how that piece in particular works:
He starts with a 16 bar series of five phrases — everything about that piece revolves around the number 16 — and the length of each is laid out in the following pattern:
From this pattern we can build the first section by reiterating it 4 times, since the first phrase length number is 4:
Now take a new 16-bar series of phrases, arranged in the same proportions. Repeat this three times, since the second phrase length number is 3. A third 16-bar series of phrases is then repeated twice, etc. In this way we can get the shape of the whole piece:
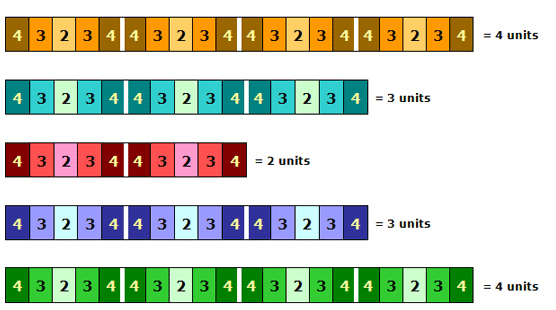
We could now iterate this process another time (this would be the third iterate), starting by repeating this whole piece four times, then another piece with the same proportional structure three times, and so on.
Combining both approaches
I decided then to attempt a combination of both formal devices: I came up with a bunch of ostinatos, and mapped them out according to a self-similar pattern, in the process which I describe below. The first difference one may note between this approach and Cage's is that while Cage only specifies the proportionality of phrases occurring in the structure, what I did was to assign each proportion to specific material, and emulated the Stravinsky-styled transitions I mentioned above by making a motif emerge from within another.
Throughout the years I have experimented with many different shapes and forms, and eventually settled on a relatively simple and straightforward one:
The structure Q consists of 3 bars of A, 1 bar of B, 2 bars of A, etc.
This means 3 bars of the element A, 1 bar of the element B, 2 bars of A, etc, and creates a 12 bar-long structure out of two distinct elements, A and B. Let's call this structure Q.
There are two main problems with using Cage's proportional durations for these purposes however. Firstly, there is the potentially excessive length of the final structure. After two iterations the structure would be 144 bars long (12 sections of 12 bars each), and after three iterations, 1728 bars long (12 × 12 ×12). Secondly, after so much repetition the pattern would eventually become predictable to an attentive listener. There are compositional ways of disguising this, of course, but that would defeat the whole purpose of this exercise entirely.
So, instead of creating 11 more structures using these same proportions, we can make just one more, which we'll call structure R. It is made up of two elements C and D:

The structure R consists of 3 bars of C, 1 bar of D, 2 bars of C, etc.
Now use Q and R to create a new structure X with the exact same proportions.
Structure X: the first unit of Q in X is made of the first two bars of Q, the second unit is made of the third and fourth bars of Q, and so on. Similarly for R.
Since we have two structures of 12 bars each, the resulting structure will have 24 bars. Therefore, in order to maintain the proportions used to create Q and R, each proportional unit of X will be two bars in length. If we peek into Structure X, we can see all the bars it's made of:

A peek into structure X.
As we can see, the first unit of Q in X is made of the first two bars of Q (that is the first two bars of element A), the second unit of Q in X is made of the third and fourth bars of Q (the third bar of element A and the first bar of element B), and so on. Similarly for the structure R.
If you look at the proportions of A, B, C and D, the whole thing is pretty chaotic-looking already, so the pattern would not become predictable. And this is only after the first iteration. Let's create a new structure Y in the same manner as X (introducing structures S and T, each composed of E, F, G and H):
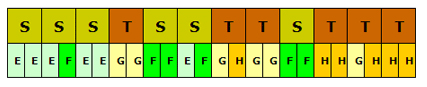
A peak into structure Y, made from structures S and T, each consisting of E, F, G and H.
Now we can map X and Y into the proportions of an even larger structure Z, where each proportional unit is 4 bars long:
The larger structure Z is made from structures X and Y.
And this is what Z is made of:
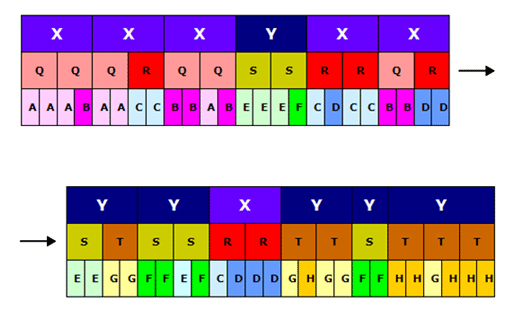
A peak into structure Z.
Are there any patterns in the occurrence of the eight original elements (A to H)? Well, there is only one, and it's not very apparent (I only found it by accident!): if we split Z down the middle, the second half is a mirror of the first, with A replaced by H, B replaced by G, C replaced by F, and D replaced by E. To all intents and purposes, we got an apparently random sequence out of a simple, straightforward process. And only 48 bars are necessary, as opposed to 1728! That's the power of fractal geometry at work: complexity created out of a simple process.
As an example of Fractal Würfelspiel at work, here is how the main structure for Coral Reef 1 was created.
- Initial cells: score mp3
- First iteration: score mp3
- Second iteration: score mp3
- Third iteration: score mp3
Finished score (this particular structure begins at around 1 min 43 secs):
coral reef symphony: part 1 (2008/9 - 10.3 MB) V.3 (definitive)
This finished structure alternates with another of identical proportions throughout the piece. The pitches were left mostly unaltered, and it is the variation of colour and orchestration that drive the piece forwards.
All tracks © Dmitry Kormann (MCPS/PRS Alliance member).
And, yes, there's nothing to stop you from bringing in another similarly generated structure to be chained with this one, and so on, theoretically forever. But in practical terms one must stop at some point. After running numerous formal experiments for over a decade, I found that in order to get that really nice feeling of balance between randomness and predictability that one gets from contemplating fractals on a computer screen — what I like to call the fractal effect — a minimum of three iterations is necessary. Coincidentally, Harlan Brothers also specifies — and here I am paraphrasing — that in order for a structure to earn the title of fractal, a minimum of 3 levels of scalar affinity must be present, as with less than that, mathematical power-law relationships will not exist (meaning we cannot see if the transformation is constant at larger scales).
I decided to name the process Fractal Würfelspiel, after Mozart's and Haydn's Würfelspiel ("game of dice") pieces. These consist of individual bars which can be arranged in any order by the throw of dice, and the result will sound musically coherent.
Working with algorithms in the creation of artworks is a process akin to gardening: we choose the layout of the garden, we plant the seeds, but it is the plants that grow themselves. Naturally, just as it happens with any other system of musical creation, coherence and artistic value is not guaranteed by the system itself, and there is no replacement for careful and thoughtful intervention from the part of the artist-gardener in the choice and shaping of (self) created original material.
About the author

Dmitry Kormann is a composer/keyboardist from São Paulo, Brazil. He works mainly on commissions for stage, screen and multimedia, which he balances with his research into algorithmic composition processes and his interests in Ambient/Trance and World Music. He is currently based in Birmingham, UK.
This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
gabriels
Reading this article reminded me of the classic "Godel, Escher and Bach" by Douglas Hofstadter. It was great to listen the fractal music rather than "imagine" how it would sound.
Anonymous
I really like fractals.
Anonymous
I am doing an extended project for AS based on fractals, due to this article :)
Anonymous
As I heard at this piece it was almost impossible not to recall Stravinsky´s music. At least that happened to me. I liked the "experiment".
Anonymous
Fourth step in Sierpinski triangle is missing. Fourth triangle shown is not correct
jtherieau
You're right. This:
https://jennifertherieau.com/wp-content/uploads/2020/04/Sierpinski-tria…
Anonymous
https://youtu.be/tSw6aZV4Sc0
Emily
Very good article. I am teaching a workshop about music and math/science in the elementary classroom. I am interested in fractals and thought that might be a great way to link the subjects together. I was initially thinking of relating fractals to the division of rhythmic notation, in a very simple way, but I also thought about having students create simple 8 beat *ostinato* patterns and then performing them in a fractal-like ternary or binary form . Your article is making me think the latter would make more sense. Thank you for your amazing research and application on this topic. I will have to study it even more.
Willeman
I stumbled across your piece "Anemonae" while Googling "fractals" some years ago and was instantly captivated by it, and though it was far removed from my traditional 'classical music' frame of reference at the time I somehow 'got' it and loved it ever since! Then, recently, I discovered that you added your "Coral reef symphony" to the site and I am just as captivated by that too.
I thought I would just let you know. I have tried to get other people interested too, but they don't seem to 'get' it... (sigh).
Steven Ross
I develop conceptual music theory and compose conceptual music pieces. May I send some to Dmitry and others?