
Mysterious number 6174

Anyone can uncover the mystery
The number 6174 is a really mysterious number. At first glance, it might not seem so obvious. But as we are about to see, anyone who can subtract can uncover the mystery that makes 6174 so special.
Kaprekar's operation
In 1949 the mathematician D. R. Kaprekar from Devlali, India, devised a process now known as Kaprekar's operation. First choose a four digit number where the digits are not all the same (that is not 1111, 2222,...). Then rearrange the digits to get the largest and smallest numbers these digits can make. Finally, subtract the smallest number from the largest to get a new number, and carry on repeating the operation for each new number.
It is a simple operation, but Kaprekar discovered it led to a surprising result. Let's try it out, starting with the number 2005, the digits of last year. The maximum number we can make with these digits is 5200, and the minimum is 0025 or 25 (if one or more of the digits is zero, embed these in the left hand side of the minimum number). The subtractions are:
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
When we reach 6174 the operation repeats itself, returning 6174 every time. We call the number 6174 a kernel of this operation. So 6174 is a kernel for Kaprekar's operation, but is this as special as 6174 gets? Well not only is 6174 the only kernel for the operation, it also has one more surprise up its sleeve. Let's try again starting with a different number, say 1789.
9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
We reached 6174 again!

A very mysterious number...
When we started with 2005 the process reached 6174 in seven steps, and for 1789 in three steps. In fact, you reach 6174 for all four digit numbers that don't have all the digits the same. It's marvellous, isn't it? Kaprekar's operation is so simple but uncovers such an interesting result. And this will become even more intriguing when we think about the reason why all four digit numbers reach this mysterious number 6174.
Only 6174?
The digits of any four digit number can be arranged into a maximum number by putting the digits in descending order, and a minimum number by putting them in ascending order. So for four digits a,b,c,d where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0
and a, b, c, d are not all the same digit, the maximum number is abcd and the minimum is dcba.
We can calculate the result of Kaprekar's operation using the standard method of subtraction applied to each column of this problem:
| a | b | c | d | |
| - | d | c | b | a |
|
|
||||
|---|---|---|---|---|
| A | B | C | D | |
which gives the relations
| D = 10 + d - a (as a > d) |
| C = 10 + c - 1 - b = 9 + c - b (as b > c - 1) |
| B = b - 1 - c (as b > c) |
| A = a - d |
for those numbers where a>b>c>d.
A number will be repeated under Kaprekar's operation if the resulting number ABCD can be written using the initial four digits a,b,c and d. So we can find the kernels of Kaprekar's operation by considering all the possible combinations of {a, b, c, d} and checking if they satisfy the relations above. Each of the 4! = 24 combinations gives a system of four simultaneous equations with four unknowns, so we should be able to solve this system for a, b, c and d.
It turns out that only one of these combinations has integer solutions that satisfy 9 ≥ a ≥ b ≥ c ≥ d ≥ 0. That combination is ABCD = bdac, and the solution to the simultaneous equations is a=7, b=6, c=4 and d=1. That is ABCD = 6174. There are no valid solutions to the simultaneous equations resulting from some of the digits in {a,b,c,d} being equal. Therefore the number 6174 is the only number unchanged by Kaprekar's operation — our mysterious number is unique.
For three digit numbers the same phenomenon occurs. For example applying Kaprekar's operation to the three digit number 753 gives the following:
753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
The number 495 is the unique kernel for the operation on three digit numbers, and all three digit numbers reach 495 using the operation. Why don't you check it yourself?
How fast to 6174?
It was about 1975 when I first heard about the number 6174 from a friend, and I was very impressed at the time. I thought that it would be easy to prove why this phenomenon occurred but I could not actually find the reason why. I used a computer to check whether all four digit numbers reached the kernel 6174 in a limited number of steps. The program, which was about 50 statements in Visual Basic, checked all of 8991 four digit numbers from 1000 to 9999 where the digits were not all the same.
The table below shows the results: every four digit number where the digits aren't all equal reaches 6174 under Kaprekar's process, and in at most seven steps. If you do not reach 6174 after using Kaprekar's operation seven times, then you have made a mistake in your calculations and should try it again!
| Iteration | Frequency |
|---|---|
| 0 | 1 |
| 1 | 356 |
| 2 | 519 |
| 3 | 2124 |
| 4 | 1124 |
| 5 | 1379 |
| 6 | 1508 |
| 7 | 1980 |
Which way to 6174?
My computer program checked all 8991 numbers, but in his article Malcolm Lines explains that it is enough to check only 30 of all the possible four digit numbers when investigating Kaprekar's operation.
As before let's suppose that the four digit number is abcd, where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0.
Let us calculate the first subtraction in the process. The maximum number is 1000a+100b+10c+d and the minimum number is 1000d+100c+10b+a. So the subtraction is:
1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)
The possible value of (a-d) is from 1 to 9, and (b-c) is from 0 to 9. By running through all the possibilities, we can see all the possible results from the first subtraction in the process. These are shown in Table 1.
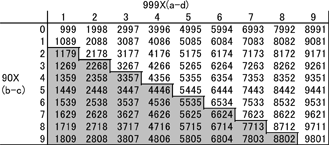
Table 1: Numbers after the first subtraction in Kaprekar's process
We are only interested in numbers where the digits are not all equal and
a ≥ b ≥ c ≥ d,
therefore we only need to consider those where (a-d) ≥ (b-c). So we can ignore the grey region in Table 1 which contains those numbers where
(a-d) < (b-c).
Now we arrange the digits of the numbers in the table in descending order, to get the maximum number ready for the second subtraction:
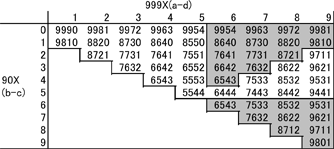
Table 2: Maximum numbers, ready for the second subtraction
We can ignore the duplicates in Table 2 (the grey regions), and are left with just 30 numbers to follow through the rest of the process. The following figure shows the routes which these numbers take to reach 6174.
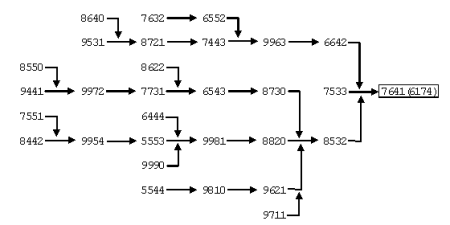
How these 30 numbers reach 6174
From this figure you can see how all the four digit numbers reach 6174 and reach it in at most seven steps. Even so I still think it is very mysterious. I guess Kaprekar, who discovered this number, was extremely clever or had a lot of time to think about it!
Two digits, five digits, six and beyond...
We have seen that four and three digit numbers reach a unique kernel, but how about other numbers? It turns out that the answers for those is not quite as impressive. Let try it out for a two digit number, say 28:
82 - 28 = 54
54 - 45 = 9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 = 9
It doesn't take long to check that all two digit numbers will reach the loop 9→81→63→27→45→9. Unlike for three and four digit numbers, there is no unique kernel for two digit numbers.
But what about five digits? Is there a kernel for five digit numbers like 6174 and 495? To answer this we would need to use a similar process as before: check the 120 combinations of {a,b,c,d,e} for ABCDE such that
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
and
abcde - edcba = ABCDE.
Thankfully the calculations have already been done by a computer, and it is known that there is no kernel for Kaprekar's operation on five digit numbers. But all five digit numbers do reach one of the following three loops:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
As Malcolm Lines points out in his article, it will take a lot of time to check what happens for six or more digits, and this work becomes extremely dull! To save you from this fate, the following table shows the kernels for two digit to ten digit numbers (for more see Mathews Archive of Recreational Mathematics). It appears that Kaprekar's operation takes every number to a unique kernel only for three and four digit numbers.
| Digits | Kernel |
|---|---|
| 2 | None |
| 3 | 495 |
| 4 | 6174 |
| 5 | None |
| 6 | 549945, 631764 |
| 7 | None |
| 8 | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| 10 | 6333176664, 9753086421, 9975084201 |
Beautiful, but is it special?
We have seen that all three digit numbers reach 495, and all four digit numbers reach 6174 under Kaprekar's operation. But I have not explained why all such numbers reach a unique kernel. Is this phenomenon incidental, or is there some deeper mathematical reason why this happens? Beautiful and mysterious as the result is, it might just be incidental.
Let's stop and consider a beautiful puzzle by Yukio Yamamoto in Japan.
If you multiply two five digit numbers you can get the answer 123456789. Can you guess the two five digit numbers?
This is a very beautiful puzzle and you might think that a big mathematical theory should be hidden behind it. But in fact it's beauty is only incidental, there are other very similar, but not so beautiful, examples. Such as:
(We can give you a hint to help you solve these puzzles, and here are the answers.)
If I showed you Yamamoto's puzzle you would be inspired to solve it because it is so beautiful, but if I showed you the second puzzle you might not be interested at all. I think Kaprekar's problem is like Yamamoto's number guessing puzzle. We are drawn to both because they are so beautiful. And because they are so beautiful we feel there must be something more to them when in fact their beauty may just be incidental. Such misunderstandings have led to developments in mathematics and science in the past.
Is it enough to know all four digit numbers reach 6174 by Kaprekar's operation, but not know the reason why? So far, nobody has been able to say that all numbers reaching a unique kernel for three and four digit numbers is an incidental phenomenon. This property seems so surprising it leads us to expect that a big theorem in number theory hides behind it. If we can answer this question we could find this is just a beautiful misunderstanding, but we hope not.
Note from the editors: many readers noticed that repeatedly adding up the digits of any of the kernels of Kaprekar's operation always equals 9. Find out why in this follow-up to the article.
References
- Kaprekar, D. R., "Another Solitaire Game", Scripta Mathematica, vol 15, pp 244-245 (1949)
- Gardner, Martin, "The Magic Numbers of Doctor Matrix", Japanese version, Tokyo: Kinokuniya (1978)
- Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers..., Bristol: Hilger (1986)
- Nishiyama, Yutaka, Kurashi no Algorithm, Kyoto: Nakanishiya (1993)
About the author

Yutaka Nishiyama is a professor at Osaka University of Economics, Japan. After studying mathematics at the University of Kyoto he went on to work for IBM Japan for 14 years. He is interested in the mathematics that occurs in daily life, and has written seven books about the subject. The most recent one, called "The mystery of five in nature", investigates, amongst other things, why many flowers have five petals. Professor Nishiyama is currently visiting the University of Cambridge.
Comments
Anonymous
I would think 9 is the absolute root kernel number.
on the two digit example the sum adds up to 9.
if you add 6174 you get 18 thus 9.
even further you can take 9 down to 3.
the mystery of 5 is in the sacred geometry of the golden ratio.
which is a simple mathematical explanation of remaining numbers and the outward spiral and unfolding of the universe mathematically. five is a spiral symbolically. and in five there are three elements and two polar opposites thus 2:3=5 or 1:1:2:3:5 two and three make five but not one and one. this on whole two polars and three elements.?
I'd like to know more......
starseed
9 is fascinating. you tube "the 9 code" and it will blow your mind. Nikola Tesla believed 3 & 6 were yin & yang while 9 represented the S curve going down the middle. 9 seems to be the ultimate "zen" or "balancer" ...in numerology, 9 is the only number that connects to all numbers. why though? is 9 godly? this is the real mystery imo. Tesla was close...
Anonymous
The article says the same phenomenon occurs with three digit numbers.
Well, this does not seem to be true.
Try with 321 and you'll see it loops...
Gerry
Anonymous
Are you sure about that? When I calculated beginning with 321, the steps went as follows: 321, 198, 792, 693, 594, 495.
Anonymous
Please check the number 6086
In my calculation (all the possible numbers for these four digits) takes up to nine steps to reach 6174 ; which itself is a multiple of 9.
Now why only this takes up to ninth step may be important.
I don't know why; but I have a feeling that it has to do something with the following math puzzle:
1. Take up a number of any digit length.
2. Leave 18 rows empty.
3. write in the 20th row sum of all these unfilled numbers.
4. The sum would always be reached by adding 9 to left of the number in first row; taking rest of the digits same till tens then subtract 9 from the ones. ( Or You may require to adjust the tens with this subtraction.)
5. Then ask the person you're playing with to write another number in second row of same digit length as first.
6. Then in third row you write your number as to make the sum of two rows as 9,99,999,9999....
For Instance:
My friend take up a number 2986.
I would leave another 18 row empty. In row # 20 I write the answer: 92977
now in second row my friend wrote 3342; while I write in 6657 in row # 4 (sum of row # 3 & 4 is 9999)
then repeat the same process 09 more times (first he write a number then I write mine to make the two row sum to be 9999)
Now go check the total which was written long before the whole series of numbers has been written.
2986 My Friend
3342 My Friend
6657 Me
1234 My Friend
8765 Me
0000 My Friend
9999 Me
0932 My Friend
9067 Me
9876 My Friend
0123 Me
1111 My Friend
8888 Me
5003 My Friend
4996 Me
0001 My Friend
9998 Me
2000 My Friend
7999 Me
--------
92977
=====
Please let me know; if this has something to do with 6174. And 6174 divided by 9 gives 686. may be this has something to do too.
Because each new derived number is multiple of nine and hence we reach multiple 686 times to get to 6174.
Kashif Ali Qureshi
Dubai, United Arab Emirates
+971-55-2594599
ksf.110@gmail.com
Rich
Hi Kashif,
I saw your post and your question as to whether the math trick has anything to do with the number 6174. It doesn't. The trick is based on adding a complementary value to each of your friend's values to ensure that the final sum will be the same as the predicted sum. I'll explain why.
The predicted sum will always be accurate because it's fixed that way, by the choice of the number you always add under your friend's number to make it add up to a number composed of all 9's.
So let 'n' denote the number of digits in the number on line 1.
There will be 18 blank lines below this number.
The final sum is predicted as 9<digits of original number up until the final two, final two digits - 9>.
Each of the 9 pairs of numbers (your friend's and yours) will always be n 9's long, as defined by your rules because you're choosing YOUR number to make this happen, dependent on the number your friend writes down.
This means that there will be 9 pairs of numbers whose sum is composed of n 9's. Which is the same as saying there will be 9 pairs whose sum is 10^n - 1, which is 9 * (10^n - 1), which is the same as inserting a 9 to the beginning of the original number, and then subtracting 9 from the result.
In other words, for a 4 digit number, you're making each pair of numbers add to 10000 - 1 = 9999, and this is the same as adding 10000 nine times, and then subtracting 1 nine times, once for each pair of numbers (your friend's and yours). So you end up adding 90000 and then subtracting 9, which you do in step 4.
For example, with a 4 digit number (like in your example), where w, x, y and z can be any 4 digits, and wxuv is the number wxyz minus 9 as you describe in step 4, and you get this:
line 1: wxyz
line 2 & 3:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 4 & 5:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 6 & 7:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 8 & 9:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 10 & 11:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 12 & 13:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 14 & 15:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 16 & 17:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
line 18 & 19:+ 9999 = 10000 - 1 your friend's number + your number : 9999 = 10000 - 1
------ ------ ---
line 20: 9wxuv = wxyz + 90000 - 9 which is what your forced prediction of the sum is.
I hope this helps explain why your math trick results in the predicted sum the way it does. Good luck in life and I hope your interest in math never fades.
Anonymous
When I was at college in the '80 in Derbyshire this was something our computer studies teacher talked about, he had read an article in a forth magazine about this and described it as being 6174 as the center of a series of concentric rings when plotted as a scatter diagram.
After listening to him prattle on about it for so long I eventually set out to prove that he didn't know what he was talking about (not unusual). So on the first day I wrote a program to calculate the route to 6174 for all 4 digit numbers, unfortunately I only had 32k of ram on my home machine and no floppy and I also needed 20k for high resolution graphics. Clearly since any calculation with the same digits would yield the same result I used 4 different FOR loops to reduce the storage requirement.
so
for a= 9 to 0
for b= a to 0
for c= b to 0
for d =c to 0
This allowed me to store and plot the results and it was nothing like as described. Apparently, my teacher explained the scatter diagrams had been rotated to make the plot of concentric rings, LOL
Anyway I said to my teacher that next I would plot the steps for all 4 digit numbers as the start of my proof investigation, when I came into college the following day my teacher said that he has passed my original ideas to the high level course and my work was a waste of time. I pointed out that in their plot they found that most numbers were not a route to 6174 and so were a jumble this as I had discussed the problem with my father who pointed out that the result of this operation is always a multiple of the base -1. Again I was finding storage a problem so I used the model discussed in the forth magazine to keep things simple, i.e. order digits high to low then reading left to right subtract 4rd digit from 1st and 3rd from second so for 7641 that would give the model 62. All numbers with model 62 in base 10 give 6174 as a result in 1 operation. Other models also share the same number of steps to reach that number. So plotting just the models you can see a much smaller graph and this moved me closer to being able to say how many steps would be required before reaching 6174.
So my question is, has anyone else produced the proof for this and answered why the numbers act this way to reach 6174 and also why 5 digits for example make a ring instead of a single number? after my experiences with my teacher I haven't published or discussed my own work on this with anyone else.
Anonymous
I read about this in Parc, S., “50 Visions of Mathematics”, Oxford University Press, (2014) and I wondered if this was true for any number base rather than just base 10.
On trying three digit numbers in octal and hexadecimal I found that they each had an equivalent kernel. This led me to solve the equations for finding the kernel, but using a variable, β, for the number base rather than restricting it to decimal numbers.
The results were as follows:
For two digit numbers there is a kernel if the base is of the form 3*(n – 1) + 5
For three digit numbers there is a kernel if the base is even i.e. of the form 2*n
For four digit numbers there is a kernel if the base is of the form 5*n, though there are kernels for base 2 and base 4.
For five digit numbers there are kernels for bases of the form 3*n
As I was using the computer algebra add-on for Microsoft Word I chose not to solve individually the hundreds of equations for six digit numbers. However, solving the equations based on the base-ten six digit numbers I did find that there are kernels for bases of the form 9*n + 8, 2*n, 15*n + 10, and 2*(n + 2).
In the above n takes the values 0, 1, 2, ...
I haven’t a proof, but it does seem likely that for any value with 3*n digits and an even base, there is a kernel which has n digits of value β – 1, β/2, and β/2 – 1. This is true for three digit numbers, six digit numbers, and some nine and twelve digit numerical examples I’ve tried.
I’ve not seen any references to this so I thought I would post these results as they may be of interest to other readers.
Philip Hickin
UK
janne_PL
Hi there Philip!
I made some brute force computing for test of four digit numbers with different bases up to 40. The principle for presentation is extrapolation of the method used to present HEX code: A = 10, B = 11 ….. F = 15, G = 16 … Z = 35, [ = 36, … ^ = 39, _ = 40.
I found that only bases 5, 10 and 40 terminate to one value: 3032 (=dec 392), 6174 and O7VG (= dec 1548456) respectively with max number of loops 4, 7 and 21 respectively.
When it comes to base = 20, loop terminates to C3F8 (= dec 97508) for many start values with max number of loops = 10
Base 15, 30, 35 do not terminate to one value.
Below a sample of loops for different bases. “…” means that loop is unterminated and will continue for ever. “…” is printed after a value in the last position N when it has been detected earlier in the loop in position N-2 or earlier. E.g. the loop
0045 5311 4132 3043 3552 3133 1554 4042 4132 ...
will continue for ever like
0045 5311 4132 3043 3552 3133 1554 4042 4132 3043 3552 3133 1554 4042 4132 3043 3552 3133 1554 4042 4132 etc
All bases are not included in this comment, but are produced in the program. I’m thinking of extending the number of digits to be variable too…
All bases have been given a random start value within the definition area, and 10 loops are printed. All loops are not presented in this comment.
Kaprekar's constant for BASE = *
***********************************************************
Base = 2:
1001 1001
1010 1001
1011 0111
1100 1001
1101 0111
1110 0111
0001 0111
0010 0111
***********************************************************
Base = 3:
0010 0222 1221 1012 1221 ...
0011 1012 1221 1012 ...
0012 2011 1221 1012 1221 ...
0020 1221 1012 1221 ...
***********************************************************
Base = 4:
3321 2022 1332 2022 ...
3322 1023 3021
3323 0333 2331 2022 1332 2022 ...
3330 2331 2022 1332 2022 ...
3331 1332 2022 1332 ...
3332 0333 2331 2022 1332 2022 ...
***********************************************************
Base = 5:
0140 4031 4121 3032
0141 3441 3032
0142 4031 4121 3032
0143 4121 3032
0144 4211 3032
0200 1443 3032
0201 2033 3032
0202 2123 1443 3032
0203 3122 1443 3032
0204 4121 3032
***********************************************************
Base = 6:
0051 5041 5221 3552 3133 1554 4042 4132 3043 3552 ...
0052 5131 4132 3043 3552 3133 1554 4042 4132 ...
***********************************************************
Base = 10:
0860 8532 6174
0861 8442 5994 5355 1998 8082 8532 6174
0862 8352 6174
0863 8262 6354 3087 8352 6174
0864 8172 7443 3996 6264 4176 6174
0865 8082 8532 6174
0866 7992 7173 6354 3087 8352 6174
0867 8082 8532 6174
0868 8172 7443 3996 6264 4176 6174
0869 9171 8532 6174
***********************************************************
Base = 15:
0796 90D6 D2B2 B854 72B8 90D6 ...
0797 8EE6 8587 30DC D852 B2B4 9676 30DC ...
0798 90D6 D2B2 B854 72B8 90D6 ...
***********************************************************
Base = 16:
0C09 C864 81D8 BFF4 B3B5 8598 3FFC C2C4 A776 3FFC ...
0C0A C954 83B8 7FF8 8688 1FFE E0E2 EB32 C774 7FF8 ...
0C0B CA44 8598 3FFC C2C4 A776 3FFC ...
***********************************************************
Base = 20:
0566 60IE I7B2 G3F4 DA87 61HE G7B4 C3F8
0567 70ID I5D2 G7B4 C3F8
0568 80IC I3F2 GB74 C3F8
0569 90IB I1H2 HE43 E996 7JJC C6C8 63FE C7B8 52GF E996 ...
056A A0IA HJJ2 H1H3 GD54 C7B8 52GF E996 7JJC C6C8 63FE C7B8 ...
056B B0I9 I1H2 HE43 E996 7JJC C6C8 63FE C7B8 52GF E996 ...
056C C0I8 I3F2 GB74 C3F8
056D D0I7 I5D2 G7B4 C3F8
056E E0I6 I7B2 G3F4 DA87 61HE G7B4 C3F8
056F F0I5 I992 FJJ4 F3F5 C998 3JJG G2G4 EB76 83FC C3F8
***********************************************************
Base = 39:
0VZZ Z3Y4 WT87 PKHE B2ZS XGL6 R4XC TENA J8TK L0\I \2Z2 ZW54 VQB8 NENG 96VU PKHE ...
0VZ[ [3Y3 XU76 RMFC F6VO P8TE LARI H2ZM X4X6 TQBA JENK 90\U \KH2 Z2Z4 XU76 ...
***********************************************************
Base = 40:
0I4A I5XM S3ZC WFN8 O7VG
0I4B I6WM Q3ZE WBR8 OFNG 96WV QLHE C3ZS WFN8 O7VG
0I4C I7VM O3ZG W7V8 PMGF A5XU SJJC F^^O OEOG A7VU OJJG 7^^W W6W8 QNFE C7VS OFNG 96WV QLHE C3ZS WFN8 O7VG
0I4D I8UM M3ZI W3Z8 WNF8 O7VG
0I4E I9TM K3ZK V^^8 V7V9 OLHG 83ZW WNF8 O7VG
0I4F IASM I3ZM W3Z8 WNF8 O7VG
0I4G IBRM G3ZO W7V8 PMGF A5XU SJJC F^^O OEOG A7VU OJJG 7^^W W6W8 QNFE C7VS OFNG 96WV QLHE C3ZS WFN8 O7VG
0I4H ICQM E3ZQ WBR8 OFNG 96WV QLHE C3ZS WFN8 O7VG
0I4I IDPM C3ZS WFN8 O7VG
0I4J JDPL C1\S [FN4 W7V8 PMGF A5XU SJJC F^^O OEOG A7VU OJJG 7^^W W6W8 QNFE C7VS OFNG 96WV QLHE C3ZS WFN8 O7VG
Anonymous
Let's omit the first stage of Kaprekar's algorithm and just look at what happens when the only rearrangement is reversing the digits in three of the numbers he looks at and doing a repeated operation.
Find the absolute difference between a number and its reverse, and then the difference between that and its reverse, and so on.
2005, 2997, 4995, 999
1789, 8082, 5274, 549, 396, 297, 495, 99
6174, 1458, 7083, 3276, 3447, 3996, 2997, 4995, 999
The absolute difference between the reverses of these repnines gives us our kernel, which is zero. That's true of all palindromes of course, though the operation in the algorithm producing a palindrome won't necessarily lead to a kernel. For example, consider summing them instead
2005, 7007
1789, 11660, 18271, 35552, 61105, 111221, 233332
6174, 10890, 20691, 40293, 79497
Lastly standard number line subtraction:
2005 ... (17 steps!) ... -8939779398
1789, -8082, -10890, -20691, -40293, -79497
6174, 1458, -7083, -10890, -20691, -40293, -79497 (A negative number can be regarded as a palindrome, eg -121 = 0-121-0)
Look at 6174 still behaving mysteriously, what's more in cahoots with that other notorious number 1089.
2005, 7007
Anonymous
Dear Mr Yutaka Nishiyama
Hello, I'm Asra Rezafadaei.l am 14 years old. l'm an Iranian student.I solved Mysterious number 6174 and my teacher accepted it.
If you read this pleas write to me and I send the answer for you.
My E-mail:gh.fadae1378@gmail.com
Anonymous
Hi all if you use the numbers 221 & 122 it does not result in 495 but rather in 99.
Marianne
That's true, but you then need to carry on, treating 99 as the 3-digit number 099. You then continue by subtracting 099 from 990, etc. Eventually you will reach 495.
Anonymous
Add the kernel 495 to its reverse, 594, and you get another famously mysterious number 1089. Do the same with 6174 and get 10890, (which is also the result of R&A 1089). R&A 549945 = 1099890, R&A 631764 = 1098900.
Chris G
Anonymous
Dear Sir,
do numbers with six digits >always< reach one of the kernels 549945 or 631764? I tried 789102 as an arbitrary number to start with, but my program yielded the following periodic numbers:
1. round: 987210 - 12789 = 974421
2. round: 974421 - 124479 = 849942
3. round: 998442 - 244899 = 753543
4. round: 755433 - 334557 = 420876 <-
5. round: 876420 - 24678 = 851742
6. round: 875421 - 124578 = 750843
7. round: 875430 - 34578 = 840852
8. round: 885420 - 24588 = 860832
9. round: 886320 - 23688 = 862632
10. round: 866322 - 223668 = 642654
11. round: 665442 - 244566 = 420876 <-
Is it a flaw in the program or haven't I yet correctly understood the meaning of your explanations given above?
Thank you!
Mysterious
It's pretty funny that all kernel numbers above 3 will make a 10 if you put the first and the last digit together. Only the 3 don't like being 10. It realy wanna be that 9.
shoutofgaia
Does it surprise anyone that if we treat all numbers from 0 (0000) as four digits up to 9999 we end up at 6174 (excluding the series where numbers are the same), which is pretty darn close to the golden ratio when divided by the whole sample number (0.6180).
Noémio Ramos
You can see the link about that:
http://www.gilvicente.eu/6174.html
FrantzelasG
I wonder could this toy model teach us anything about Collatz conjecture?
Martin Crom
Hi,
The maximum common divisor of 495 and 6174 is 9.
In the 9 scale you can find all the 1467,1476,4167,4617 .. etc iterations.
In a magic scope: +495 + 6174 = 6669. +6669/9 (MCD)= 714. 714 is considered lucifer number.
Best,
Martin
Martín Crom
Some thoughts
*11+22+33+44+55+66+77+88+99=495
*111+222+333+444+555+666+777+888+999+1110+69=6174
*6174+495=6669
*Square root of (1467,1476,1647,1674....) Only hole numbers 42 and 69. 42*42=1764 69*69=4761
* 69+42=111
* 0000,1111,2222,3333,4444,5555,6666,7777,8888,9999. 6174 should have a property similar from the rest of them.
(1467,1476,1674,1647 ...etc)/5555 -average of above, 6174 is 1,111. If variations are in order, 1,111 is in the middle of the variations.
* All numbers in Kaprekar process are divisible by 9.
Anonymous
Hi, the ISBN of your book includes number 6174. This was by chance or you selected it?
The Mysterious Number 6174; One of 30 Amazing Mathematical Topics in Daily Life
ISBN-13: 978-4768761748, ISBN-10: 4768761747
DaveC426913
Authors don't get to pick ISBN numbers. So it is a (very) happy coincidence.
P.S.: A member on my science forum posted the 6174 puzzle (without identifying it to pique curiosity).
I programmed the entire 9999-line output in JavaScript. Then a little research led me here.
It fascinates me that there many be no deeper meaning to this mathematical oddity.
Adam.Antithesis at gmail dot com
Today is Friday 11-10-2017 in the US.
To the Author of the blog:
Here below is sequence 7641, an exact 4 digit sequence in the famous repeating 24 digit Digital Root Fibonacci Sequence. Below, I'll use a date utilizing a special date formula to arrive at a 2 digit result, but a 4 digit result is more interesting; this number was not expected; it's just the result of some inspired calculation methods.
07-28-2017
Using only Addition and Digital Root and Fibonacci Sequences
::
07-28 6017
--------------^--------------
7+1=(8) + [5]= (4):+= [9]
7+1=(8) + [1]= (9):+= [1]
--------------v----------------
7-28 2017
Now, do vertical DR & FS on the above bracketed numbers
.......(7) (6) (4) (1)
Do the same for 7-27-2017, and a 4 digit sequence result is 5628, also exact.
With both 4 digit numbers, those are 8 in exact order in the 24 repeating digit sequences in DR FS.
7641 and 5628 can be translated to English letters (A=1, B=C....J_10 as DR 1, Z_26 = as DR 8 etc).
Since F=6, O=15, and X=24, 6 above can be F, or O or it an be X...
7 can be G, P or Y...(or PIG instead of PYG) since letter I is dr 9 and does not taint the calculation...
7641 5628
GODA EOBH
Likewise, adding an R which is letter 18 which is DR 9, also does not taint the calculation.
And, when you re-arrange those letters, you can see this result:
"HE GOD BOAR"
Just number fun?.... Is this all just for our amusement or for or edification?
Thanks,
This Adam
Martín Crom
Hi,
(11+99)=110
(22+88)=110
(33+77)=110
(44+66)=110
Total=440
55+440=495
If you see how this works in the calculator keyboard you will see all is around number five.
hasan
Please explain the pattern of the following numbers and what is your prediction of the next four digits?
Thanks
8501
6656
6103
9166
4337
7003
6531
9210
3159
1024
i_dikov@yahoo.com
Ivan Dikov, 2019.02.04, Sofia, Bulgaria
//getKaprekarNumber(4); //6174
//getKaprekarNumber(5); //not found
//getKaprekarNumber(6); //549945, 631764
//getKaprekarNumber(7); //not found
//getKaprekarNumber(8); //63317664, 97508421
//getKaprekarNumber(9); //554999445, 864197532
//getKaprekarNumber(10); //6333176664, 9753086421, 9975084201
//getKaprekarNumber(11); //86431976532
//getKaprekarNumber(12); //555499994445, 633331766664, 975330866421, 997530864201, 999750842001
//getKaprekarNumber(13); //8643319766532
//getKaprekarNumber(14); //99997508420001, 99975308642001, 99753308664201, 97755108844221, 97533308666421, 63333317666664
//getKaprekarNumber(15); //555549999944445, 864333197666532
//getKaprekarNumber(16); //9999975084200001, 9999753086420001, 9997533086642001, 9977551088442201, 9975333086664201, 9775531088644221, 9753333086666421, 6333333176666664
//getKaprekarNumber(17); //98765420987543211, 86433331976666532
//getKaprekarNumber(18); //999999750842000001, 555554999999444445, 999997530864200001, 999975330866420001, 999775510884422001, 999753330866642001, 886644219977553312, 997755310886442201, 997533330866664201, 977553310886644221, 975333330866666421, 633333331766666664
//getKaprekarNumber(19); //9987654209875432101, 9876543209876543211, 8643333319766666532
//getKaprekarNumber(20); //99999997508420000001, 99999975308642000001, 99999753308664200001, 99997755108844220001, 99997533308666420001, 99977553108864422001, 99975333308666642001, 88664432199776553312, 99775533108866442201, 99753333308666664201, 97775551108884442221, 97755333108866644221, 97533333308666666421, 63333333317666666664
//getKaprekarNumber(21); //555555499999994444445, 999876542098754321001, 998765432098765432101, 987654332098766543211, 864333333197666666532
//getKaprekarNumber(22); //9999999975084200000001, 9999999753086420000001, 9999997533086642000001, 9999977551088442200001, 9999975333086664200001, 9999775531088644220001, 9999753333086666420001, 9997755331088664422001, 9997533333086666642001, 9977755511088844422201, 8866443321997766553312, 9977553331088666442201, 9975333333086666664201, 9777555311088864442221, 9775533331088666644221, 9753333333086666666421, 6333333333176666666664
If somebody has questions just write on email: i_dikov@yahoo.com.
Matt Carrell
Look at 6 and 9 digit numbers.. 6 and 9 are 2nd and 3rd multiples of 3..
Moreover, the results for 6 an 9 digits are all containing the numbers 495 or 6174 and then taking the 6 digit versions which add extra digits by putting the original numbers backwards interspaced with itself.. For 495, _4 _9_5 woven with 5_9_4_ becomes the mirrored number 549945…. and for 6174 then 6_17_4 and the added two digits 3 and 6 only _3__6_ which is only one off from backwards first and last digits of 4 and 6 becoming 631764.
Now for the related NINE digit versions, you take the six digit versions and stutter the numbers as such
549945 becomes 5_49_94_5 adding the backwards of 495 interspersed as _5__9__4_ to become 554999445 and
864197532 contains _641_753_. or 641753 which is 631764 only shifted up or down one for three of the digits.
Then the EIGHT and TEN digit numbers are related somehow to the 4 and 6 digits numbers for at least the first answer which is the same as the eight digit number answer just stuttering in another mirrored copy of the digits 3 and 6 again. The middle number unsure how that might derive till. The last ten digit answer clearly contains the last eight digit answer as such: 9975084201. =. _9750842_1 ….
And don't get me started on the patterns for the added digits and evens and odds… ;)
Your link to "Mathews Archive of Recreatrional Mathematics" is no longer good. The closest related page I could find by Googling was the one here:
https://www.primepuzzles.net/thepuzzlers/Schnider.htm
I saw some mentions of Kaprekar snooping through lower links but none which addressed the numbers 495 or 6174.
OK, totally done trying to skull-out over this odd mathematical number and its relationships… ;)
Rajhans Kumar Deo
9564
9654
4569
5085
8550
558
7992
9972
2779
7193
9731
1379
8352
8532
2358
5994
9954
4559
5395
9553
3559
5994
Sergio Ap. Paganoti
Calculation: 9972-2799 = 7173 .
Shawn
In the table showing the different digits a pattern involving 495 and 6174 emerges in the higher numbers. For 6, 8, 10 digits they can all end at 6174 with a different number of 3's and 6's in the middle. 6 and 9 digits can end with 495 rearranged 2 then 3 times respectively
Carlos Gonzalez C
The quantity of 4-digits numbers that reach 6174 are 9990
Divided by the golden number is 6174.1595... the closest integer is 6174
It is not intriguing?
stewart mcneill
I keep coming back to this, wish I had appreciated the beauty of maths when I was younger!
What was that one about the boring taxi driver number too? Love that one also! Thanks!
Mike Jones
(or, ‘anagrammatic totients’ for short)
(suggested new terminology)
Definition. For numbers of a specified number of digits (padding with leading zeros if necessary), an anagrammatic totient value (or, an anagrammatic totient, for short) is a totient that is an anagram of the argument.
For example, for 4-digit numbers, Kaprekar’s constant, namely, 6174, has an anagrammatic totient, namely, 1764 (which, incidentally, is the year of Goldbach’s death).
Antonio Cimino
I have been working on perfect numbers, and my observation of this number 6174, shows the first 2 perfect numbers after 1, they are 6 and 28. which 6 can be created by the first 2 numbers 61 giving (6*1) = 6, while 74 giving (7*4) = 28. Not sure what it means yet, but just an observation.
Sarah Mukavetz
Maybe this was mentioned already, but I just noticed something that gave me chills.
Any place you divide the number 6174 then add the two numbers together it equals 9. For example, 6 + (1=7=4) =6+(1+2) =6+3=9
Then to keep going, (6+1+7) +4 =
=14 (1+4) +4
=5 +4 =9
Same if you divide the number 6174 in the middle... (6+1)+(7+4)= 9
Go ahead and try it. :) Math is fun.
Michael
The results number of iterations are {'0': 1, '1': 383, '2': 576, '3': 2400, '4': 1272, '5': 1518, '6': 1656, '7': 2184, '8': 0}??
Mike Jones
Kaprekar’s constant 6174 can be
considered to be a disguised form
of the silver ratio (that is, the
reciprocal of the golden ratio).
Rationale:
There are 9990 4-digit numbers
having at least 2 distinct digits.
The location of Kaprekar’s
constant among them is, to
4 decimal places, the silver
ratio deep among them,
the silver ratio being the
reciprocal of the golden ratio
(not to be confused with
the silver mean, also known
as the silver ratio).
That is to say, 6174/9990 is,
to 4 decimal places, 0.6180.
So, every 4-digit number, at
the beginning of the Kaprekar
process, shouts out “Hi-Yo Silver!”
Rehan Kashif
Four Numbers Max-Min=3087
Min Max Difference
1234 4321 3087
2345 5432 3087
3456 6543 3087
4567 7654 3087
5678 8765 3087
6789 9876 3087
3087*2=6174
Rob Legg
9455 begets 9455
4111 begets 9455
Pat McCarthy
9455...
9554
-4559
=4595 so ummm...
Pat McCarthy
I was amused to note that only 2 multiples of digits only have 1 sink (3:-> 495 and 4->6174)
But for all the others that have a sink, One of the solutions will contain 6, 1, 7, and 4 while the other will contain 4, 9, and 5
10 has 3 sinks. 2 of them contain 6, 1, 7, 4 and 2 of them contain 4, 9, and 5 (One sink contains both sets)
Yan Lin Aung
I am searching the basic number of gold.
In sigil,need to remove a,e,i,o,u ,
gold= 7+30+4=41 , 7+3+4=14
Dollar
Dllr=4+30+90=124, 4+3+9=16
By chemical name,XAU,X=600,if remove zeros,x=60 or 6
Abbreviation of Dollar=USD=SD=100+4=104
If remove zeros,10+4=14 or 1+4=5
The ratio of Xauusd=4:5
But many technical indicators use 14.
Is there specific number for gold or xau?
Stash
I know this really old but did any notice that each kernel when broken into individual numbers and added together then break the answer into individual numbers and add them, always gives you 9
Ex1
631764
6+3+1+7+6+=27
2+7=9
Ex 2
6174
6+1+7+4=18
1+8=9
Ex3
495
4+9+5=18
1+8=9
Ex4
554999445
5+5+4+9+9+9+4+4+5=54
5+4=9
dsect
Being an old assembler programmer, I was curious about hexadecimal. I've tried 2, 3, and 4 digit hex numbers and found that the 2 digit loops on C3 87 0F E1, the 3 digit did in fact have a kernel (7F8 = 2040 decimal), and the 4 digit had a larger loop. As suspected, after the first subtraction, adding the digits of each result gave a multiple of F (decimal 15, base - 1). Fascinating stuff...
stevieshepp
I’ve been reading this page for about 30 minutes now and trying to understand why the 7 digit kernel isn’t possible but either I’m stupid or not doing it right but I found a loop. Or is it not possible because there are just too many loops therefore not possible?