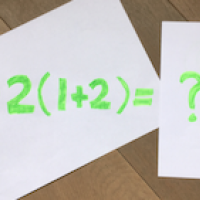
The PEMDAS Paradox
It looks trivial but it keeps going viral. What answer do you get when you calculate $6\div 2(1+2)$? This question has reached every corner of social media, and has had millions of people respond with two common answers: $1$ and $9$.
You might think one half of those people are right and the other half need to check their arithmetic. But it never plays out like that; respondents on both sides defend their answers with confidence. There have been no formal mathematical publications about the problem, but a growing number of mathematicians can explain what's going on: $6\div 2(1+2)$ is not a well-defined expression.
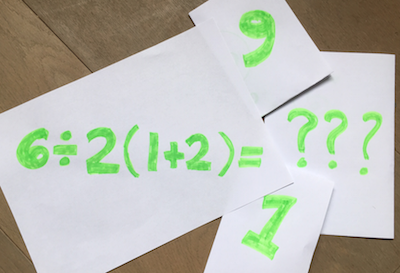
Well-defined is an important term in maths. It essentially means that a certain input always yields the same output. All maths teachers agree that $6\div (2(1+2)) = 1$, and that $(6\div 2)(1+2) = 9$. The extra parentheses (brackets) remove the ambiguity and those expressions are well-defined. Most other viral maths problems, such as $9-3\div 1/3 + 1$ (see here), are well-defined, with one correct answer and one (or more) common erroneous answer(s). But calculating the value of the expression $6\div 2(1+2)$ is a matter of convention. Neither answer, $1$ nor $9$, is wrong; it depends on what you learned from your maths teacher.
The order in which to perform mathematical operations is given by the various mnemonics PEMDAS, BODMAS, BIDMAS and BEDMAS:
- P (or B): first calculate the value of expressions inside any parentheses (brackets);
- E (or O or I): next calculate any exponents (orders/indices);
- MD (or DM): next carry out any multiplications and divisions, working from left to right;
- AS: and finally carry out any additions and subtractions, working from left to right.
Two slightly different interpretations of PEMDAS (or BODMAS, etc) have been taught around the world, and the PEMDAS Paradox highlights their difference. Both sides are substantially popular and there is currently no standard for the convention worldwide. So you can stop that Twitter discussion and rest assured that each of you might be correctly remembering what you were taught – it's just that you were taught differently.
The two sides
Mechanically, the people on the "9" side – such as in the most popular YouTube video on this question – tend to calculate $6\div 2(1+2) = 6 \div 2 \times 3 = 3\times 3 = 9$, or perhaps they write it as $6\div 2(1+2) = 6\div 2(3) = 3(3) = 9$. People on this side tend to say that $a(b)$ can be replaced with $a\times b$ at any time. It can be reduced down to that: the teaching that "$a(b)$ is always interchangeable with $a\times b$" determines the PEMDAS Paradox's answer to be $9$.
On the "1" side, some people calculate $6\div 2(1+2) = 6\div 2(3) = 6\div 6 = 1$, while others point out the distributive property, $6\div 2(1+2) = 6\div (2+4) = 6\div 6 = 1$. The driving principle on this side is that implied multiplication via juxtaposition takes priority. This has been taught in maths classrooms around the world and is also a stated convention in some programming contexts. So here, the teaching that "$a(b)$ is always interchangeable with $(ab)$" determines the PEMDAS Paradox answer to be $1$.
Mathematically, it's inconsistent to simultaneously believe that $a(b)$ is interchangeable with $a\times b$ and also that $a(b)$ is interchangeable with $(ab)$. Because then it follows that $1 = 9$ via the arguments in the preceding paragraphs. Arriving at that contradiction is logical, simply illustrating that we can't have both answers. It also illuminates the fact that neither of those interpretations are inherent to PEMDAS. Both are subtle additional rules which decide what to do with syntax oddities such as $6\div 2(1+2)$, and so, accepting neither of them yields the formal mathematical conclusion that $6\div 2(1+2)$ is not well-defined. This is also why you can't "correct" each other in a satisfying way: your methods are logically incompatible.
So the disagreement distills down to this: Does it feel like $a(b)$ should always be interchangeable with $a\times b$? Or does it feel like $a(b)$ should always be interchangeable with $(ab)$? You can't say both.

(Image from Quora)
In practice, many mathematicians and scientists respond to the problem by saying "unclear syntax, needs more parentheses", and explain why it's ambiguous, which is essentially the correct answer. An infamous picture shows two different Casio calculators side-by-side given the input $6\div 2(1+2)$ and showing the two different answers. Though "syntax error" would arguably be the best answer a calculator should give for this problem, it's unsurprising that they try to reconcile the ambiguity, and that's ok. But for us humans, upon noting both conventions are followed by large slices of the world, we must conclude that $6\div 2(1+2)$ is currently not well-defined.
Support for both sides
It's a fact that Google, Wolfram, and many pocket calculators give the answer of 9. Calculators' answers here are of course determined by their input methods. Calculators obviously aren't the best judges for the PEMDAS Paradox. They simply reflect the current disagreement on the problem: calculator programmers are largely aware of this exact problem and already know that it's not standardised worldwide, so if maths teachers all unified on an answer, then those programmers would follow.
Consider Wolfram Alpha, the website that provides an answer engine (like a search engine, but rather than provide links to webpages, it provides answers to queries, particularly maths queries). It interprets $6\div 2(1+2)$ as $9$, interprets $6\div 2x$ as $3x$, and interprets $y=1/3x$ as the line through the origin with slope one-third. All three are consistent with each other in a programming sense, but the latter two feel odd to many observers. Typically if someone jots down $1/3x$, they mean $\frac{1}{3x}$, and if they meant to say $\frac{1}{3}x$, they would have written $x/3$.
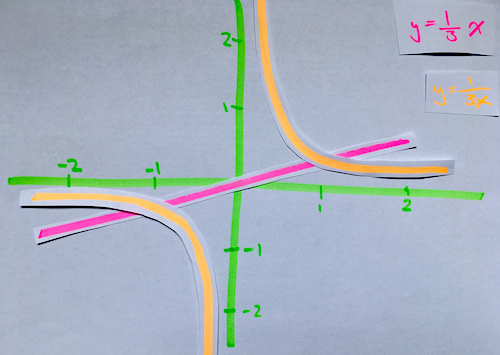
In contrast, input $y=\sin 3x$ into Wolfram Alpha and it yields the sinusoid $y=\sin (3x)$, rather than the line through the origin with slope $\sin 3$. This example deviates from the previous examples regarding the rule "$3x$ is interchangeable with $3\times x$", in favor of better capturing the obvious intent of the input. Wolfram is just an algorithm feebly trying to figure out the meaning of its sensory inputs. Kinda like our brains. Anyway, the input of $6/x3$ gets interpreted as "six over $x$ cubed", so clearly Wolfram is not the authority on rectifying ugly syntax.
On the "1" side, a recent excellent video by Jenni Gorham, a maths tutor with a degree in Physics, explains several real-world examples supporting that interpretation. She points out numerous occasions in which scientists write $a/bc$ to mean $\frac{a}{bc}$ . Indeed, you'll find abundant examples of this in chemistry, physics and maths textbooks. Ms. Gorham and I have corresponded about the PEMDAS Paradox and she endorses formally calling the problem not well-defined, while also pointing out the need for a consensus convention for the sake of calculator programming. She argues the consensus answer should be 1 since the precedence of implied multiplication by juxtaposition has been the convention in most of the world in these formal contexts.
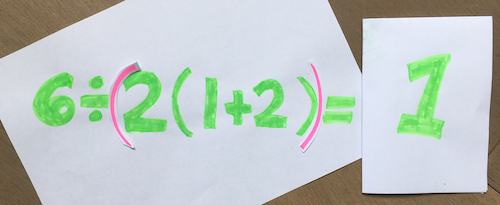
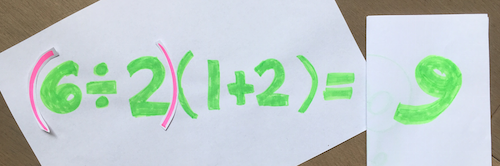
The big picture
It should be pointed out that conventions don't need to be unified. If two of my students argued over whether the least natural number is 0 or 1, I wouldn’t call either of them wrong, nor would I take issue with the lack of worldwide consensus on the matter. Wolfram knows the convention is split between two answers, and life goes on. If everyone who cares simply learns that the PEMDAS Paradox also has two popular answers (and thus itself is not a well-defined maths question), then that should be satisfactory.
Hopefully, after reading this article, it's satisfying to understand how a problem that looks so basic has uniquely lingered. In real life you should use more parentheses and avoid ambiguity. And hopefully it’s not too troubling that maths teachers worldwide appear to be split on this convention, as that’s not very rare and not really problematic, except maybe to calculator programmers.

For readers not fully satisfied with the depth of this article, perhaps my previous much longer paper won't disappoint. It goes further into detail justifying the formalities of the logical consistency of the two methods, as well as the problem's history and my experience with it.
About the author

David Linkletter
David Linkletter is a graduate student working on a PhD in Pure Mathematics at the University of Nevada, Las Vegas, in the USA. His research is in set theory - large cardinals. He also teaches undergraduate classes at UNLV; his favourite class to teach is Discrete Maths.
Comments
Anonymous
thank you for stealing my time...
Pete Martin
I have followed a lot of the comments regarding the subject expression and the controversy created. Many agree that the expression is ambiguous but some settle for either PEMDAS and the order of operations from left to right while others use juxtaposition to resolve the group first. A lot of the confusion results from the use of the obelus (:-) for division with some noting that it is a syntax error and one should use either the slash (/) or more preferably the vinculum (---) instead. However, I have seen a different way of solving the expression that uses the uncontroversial rule for how to solve the division of fractions. i.e, multiply the first fraction by the reciprocal of the second fraction. To wit: the expression 6:- 2(1+2) uses the obelus to indicate division. But all can agree that any value is equal to itself if divided by 1, so if we write the expression as 6 over 1 :- 2(1+2) over 1 then it becomes 6 over 1 x 1 over 2(1+2)[the reciprocal]. From here it does not matter which operation is chosen first, i.e to either resolve the denominator first: 6 over 6 or to divide the group factor (in this case 2) into the numerator it becomes 3 over 3, and both methods result in 1 as the answer. Any comment on this?
Shawn
When you bring something like x/yz into the discussion, you're talking apples and oranges.
In dealing with algebra, an expression like yz is known as a monomial. A monomial is defined as:
"an expression that has a single term, with variables and a coefficient. For example, 2xy is a monomial since it is a single term, has two variables, and one coefficient. Monomials are the building blocks of polynomials and are called 'terms' when they are a part of larger polynomials. In other words, each term in a polynomial is a monomial."
A monomial is a convention used in algebra that mathematicians understand to be a single unit. So when you run into something like x/yz, you know to interpret it as x divided by yz, not x divided by y and then multiplied by z.
Simply put, 2(1+2) is not a monomial, and shouldn't be treated the same way. 2(1+2) is exactly the same as 2 x (1+2) and should be treated as such.
Order of Operations is clear and is intended to bring unambiguity to math. Those of you talking about juxtaposition multiplication having a higher priority are just adding confusion to the mix.
Steve
Sin 2(3) is interpreted as Sin (2 * 3) = Sin 6 not as (Sin 2) * 3 so I respectfully disagree. Logically if ab is algebraically interpreted as (ab), {that is as the single number which is the product of a and b}, then a(-b) has to be interpreted as (a(-b)) = (-ab) which means that a(b) is as much of a monomial as ab is and therefore 2(3) is a monomial (a number is a monomial: the monomial 2X**0 = 2(1) = 2).
Dee
Shawn, you were on the right track when you said, "A monomial is a convention used in algebra that mathematicians understand to be a single unit. So when you run into something like x/yz, you know to interpret it as x divided by yz, not x divided by y and then multiplied by z."
By virtue of identifying what a monomial is, you're saying that a monomial is "glued together" by multiplication by juxtaposition -- and that a monomial does not need to be encased inside a set of parentheses to be understood as having a single value (the PRODUCT of the coefficient multiplied by the variable or variables).
In your " x/yz" example...
x=6
y=2
z=(1+2)
To solve, all you're going to do is plug in the numerical values of the variables -- which does not change the mathematical procedures at all.
With the numerical values of the variables given above, will you please show the steps to arrive at the quotient of your monomial division statement, "x/yz"?
Dev R.
As you pointed out, a construction such as "yz, "xy" or "2y" is a monomial (one term, formed by implied multiplication by juxtaposition, holding a single value which is the product of its factors). Thus, the value of the monomial term xy (or 2y) must be calculated first, before executing the division:
I do, however, take issue with your assertion that, "Simply put, 2(1+2) is not a monomial, and shouldn't be treated the same way. 2(1+2) is exactly the same as 2 x (1+2) and should be treated as such."
We both agree that "yz" is a monomial (one "unit"), even though it is not encased in parentheses. Then obviously it is understood that substituting in the numerical values for y & z does not change the value of the monomial term yz: When y=2 & z=3, then yz=2(3) and 2(3)=6, so yz=6
Thus, according to Leibniz's Law/Substitution Property of Equality, 2(1+2) or 2(3) is indeed a monomial.
from Math.net:
https://www.math.net/equality#:~:text=The%20substitution%20property%20of%20equality%20states%20that,basic%20arithmetic%20operations%20to%20demonstrate%20this%20property.
"The substitution property of equality states that for any quantities or expressions, if a=b, then substituting a or b for the other in a given expression will yield the same result."
In accordance with Leibniz's Law/Substitution Property of Equality, a number can be substituted for a letter-variable, and a letter-variable can be substituted for a number (and back and forth an infinite number of times) because the equals sign goes in both directions since the values are identical.
Given:
z=6 so 6=z
x=2 so 2=x
y=3 so 3=y
Now substituting in those equal values, one step at a time:
z÷xy=6÷xy
z÷xy=6÷2y
z÷xy=6÷2(3)
And because the equals sign goes in both directions...
6÷2(3)=z÷xy
...so everything that applied in the expression z÷xy also applies in 6÷2(3) -- including the fact that the monomial xy is not completely encased in parentheses but is understood to be one "unit," so its numerical equivalents share that same identity, since simple substitution does not change a term's or an expression's value.
so...
xy=2(3)=6
z÷xy=6÷6=1
And again, because the equals sign goes both ways...
6÷2(3)=z÷xy=6÷6=1
2(1+2) or 2(3) is indeed a monomial since there is a mathematical law which says you can substitute equal values without changing the value or meaning of the expression -- even if those equalities are in letter-variable form rather than numbers or vice-versa.
PEMDAS is a very simplified introduction to dealing with expressions with mixed operations, geared for elementary school children to give them a "running start" to deal with that situation that they had not encountered before. there is no demonstration of solved examples featuring implied multiplication by juxtaposition (how a monomial is formed) for those children, probably because it's too sophisticated a concept for them to understand at that early juncture. Thus, they are never specifically instructed to insert an explicit multiplication sign where there isn't one, and then treat each individual element as if it had nothing to do with the others. The definition of what a monomial is, how it is formed and how it works, comes later in school, when they can better understand that much more sophisticated and abstract concept.
The rules for algebra are not "different" to the basic rules of mathematics -- it's only that new information gets added, to deal with mathematical situations that they had not been exposed to up to that point. The old rules still apply -- but in a new way (with that additional information). Think of it as the explanation that a young child is given as to where babies come from -- it does not include explicit descriptions of sexual intercourse of mammals, but a few years later when they're in high school, there's a much more detailed explanation including sexual intercourse and genetics. The original information still applies but now there is a whole new context.
PEMDAS is a very simplified mathematical methodology taught to young children that they can readily understand -- a methodology with "training wheels." By high school, they can understand more sophisticated context, so the training wheels come off.
John Yoepp, PhD
There is no paradox. The expression is a well formed formula and it has the value 9 when evaluated using PEMDAS.
Bielec
The confusion is caused by order of operations, in this case, whether division or multiplication should be done first. The question, in fact, is:
6 / 2 * 3 as brackets always go first.
Instead of determining the order of operations, let's change the division into mutiplication:
6 * 1/2 * 3
Now, we only have multiplication, but let's make it even easier than that. Let's change all numbers into fractions:
6/1 * 1/2 * 3/1
We multiply fractions by multiplying the numerators:
6 * 1 * 3 = 18
and by multiplying denominators:
1 * 2 * 1 = 2
As a result, we have a fraction:
18 / 2
and the answer is 9.
Daniel
As one who majored in MAE with a minor in math and computer programming, I did find it more intuitive to treat a/bc as a/(bc). I did not until recently swap camps when I realized that in several problems where multiple operators were present, the commutative and associative properties of multiplication would go away. Not only that, if we look at another formerly ambiguous expression (for those who forget that association and commuting do not work with subtraction):
a - b + c = (a - b) + c
a - b + c ≠ a - (b + c)
Likewise:
-x² = -(x²)
-x² ≠ (-x)²
So for if nothing more than the sake of consistency:
a/bc = (a/b)(c) [where distribution still works]
a/bc ≠ a/(bc)
We all agree that the two following statements are true:
1. a/b/c = a/(bc)
2. a/b × c = (ac)/b
If a/bc = a/(bc), then a/bc = a/b/c
Which seems nonsensical to me.
But if a/bc = (ac)/b, then a/bc = a/b × c
Which to me makes more logical sense since the two sides of the equation both deal with multiplication (one implied and one expressed)
Just my $0.02
Donald
You said...
"If a/bc = a/(bc), then a/bc = a/b/c
Which seems nonsensical to me."
In fact that is completely correct - just put some numbers in...
1÷2÷3=(1/2)÷3=1/6=1/(2*3)
In the same way that distributing a minus over a bracketed term changes any + to a -, distributing a ÷ over any bracketed term changes a x to a ÷.
This is a well-known property in Maths which is covered when teaching multiplying and dividing fractions.
Someone once asked me "what is a/b/c/d?". Easy, a/bcd
James Mauro
An obelus was added to the mathematical language in the 1600's to write simple ratios. The orginal symbol for this looked like this ÷ . Eventually overtime especially with typewriters the symbol became looking like this : .
A viniculum was added shortly after an obelus and to write an equation that had an obelus into a equation using a vinculum you would write
6
6÷2×(3+3) into. _____×(3+3)
2
But this can also be written as 6:2×(3+3)
A solidus / was added to the mathematical language in the 1700's in order to write complex fractions that would normally require the use of a vinculum in the "inline fraction form". The use of a vinculum in math can easily require 3 times more paper use. The length of the equation is equal to the longest of either the denominator or numerator respectively, and even if one of the 2 is only 1 character, and the other is 32 characters long. You are wasting 31 extra characters on a vinculum and also the opossing side of the fraction. For this fact a solidus is not only a needed symbol in mathematics but also a cost saving method.
6/2(3+3) written with a vinculum would look like
6
__________
2(3+3)
Scientific calculator in the programming can switch between if they recognize a solidus or an obelus. Very expensive calculators can utilize both symbols in the same equation. Many physics professors will have 2 identical calculators with a label on each that states obelus, or solidus; or use the corresponding symbol on the label. This is done to help teach students that do not understand the difference.
If you have an equation such as ab÷cd and have a calculator set up to only solve for solidus than you need to convert that into a(b/c)d for the calculator to solve that equation correctly.
If you have an equation such as ab/cd and have a calculator only capable of solving for obelus(ratio) equation than it will need to be converted into (ab)÷(cd)
In the 1900's a printing press thought a solidus looked better than an obelus. So instead of placing the key for an obelus down as they where suppose to do, they changed the symbol and printed that mathematical text wrong. Still to this day there are many examples of this still found in high-school math text books.
For example when they have an excel spread sheet of mathematical notation a vinculum is referenced as being a horizontal or a vertical line and the horizontal symbol is removed from the symbols column. With ÷ and : symbols they are in there own column together and they both simply reference division symbols and not there intended references of being simple ratio symbols. In a column far away from obelus symbols generally next to a vinculum it has a solidus / symbol. Again only referencing it as a division symbol, instead of writing in-line fraction bar. If they could actually be used interchangeably than the orginal pre-printing company edits would have had all 3 symbols on the same excel column.
During the 1900's many public education school teachers wouldn't even have an associates degree. As a result many of the books sold to schools where never peered reviewed after printing.
A good scientific calculator not only should be able to switch between if it reads a solidus and obelus in the equation by going into setting. But also when it is set to obelus; to show an obelus on the screen. When it is set to do math in terms of a solidus than it shows a solidus on screen.
All these problems exist solely do to publishers such as wolfram misprinting mathematical textbooks. They have a web page dedicated to the fact that all peer reviewed mathematical textbooks used by people with phd. and peer reviewed by people with Phd's have the solidus and obelus meaning different things.
For this reason wolfram is not used in any college that teaches physics, programming, engineering or any other degrees that require advanced mathematics. As they would be peer reviewed and thrown out do to the level of misprinted textbooks they produce.
Instead of wolfram correcting there misprinted textbooks and printing a retraction and an apology to the mathematical community and public educational facilities, they ask others to join in with them for there misprints on there web page that dedicated to the fact that all peer reviewed advanced math text books would have 6÷2×(3+3)=18 and 6/2(3+3)=1÷2
A solidus is a necessary symbol in mathematics, it allows for easier reading of complex fractions, it saves on paper, ink.
https://mathworld.wolfram.com/Solidus.html
Paco
Ok we have that problem and 2 "plausible" answers so make a little trick.
Change the 1 to be a X.
So instead of 6/2(1+2)= you make that 2 equations:
6/2(X+2)=9 and 6/2(X+2)=1. I never reach the obvious X=1 with one of them 🤷♂️
Dee
A monomial is one term with a single value -- the PRODUCT of the coefficient multiplies by the variable (factor). An example of a monomial is "2x," which means "x" taken two times -- in other words...
2x = [ x + x }
Notice that the coefficient of 2 "disappears" when you write out the indicated additions of the monomial.
Every Basic Algebra textbook & online math tutoring website shows examples of monomials without each monomial being encased in a set of parentheses, even though the monomial is part of a larger statement. For example...
from Algebra Practice Problems. com:
https://www.algebrapracticeproblems.com/dividing-monomials/
"How to divide a monomial by a monomial"
"Any division of monomials can also be expressed as a fraction:
8x^3 y^2 z ÷ 2x^2y
[shown on the site as equal to a top-and-bottom fraction, with "8x^3 y^2 z" as the numerator & "2x^2y" as the denominator, but this comment box won't let me show it that way]
Note that an obelus was used as the original division symbol & that there were no parentheses in any part of the horizontally written monomial division statement.
--------------
In the monomial division "2x ÷ 2x ," the monomial division is actually...
[ x + x ] ÷ [ x + x ]
In the monomial division statement "2x ÷ 2x ," x = (1+2)
To solve, all you're going to do is plug in the value of "x," so the math doesn't change -- remember that multiplication by juxtaposition identifies a monomial which holds a single value, which is the PRODUCT the coefficient multiplied by the variable (factor). Please show your steps in solving the monomial division "2x ÷ 2x ," when x= (1+2).
Jean-Pierre White
Educators developed an acronym to help students remember how to apply the order of operations. Unfortunately it has a flaw, it does not consider multiplication by juxtaposition. How this came to be is unknown, it could have been deliberate or simply an oversight.
When calculators came on the scene that did apply multiplication by juxtaposition then educators had a problem. In North America manufacturers were asked to drop multiplication by juxtaposition in calculators since it created a conflict with textbooks which applied PEMDAS strictly. A few manufacturers did comply (Casio comes to mind) which resolved the conflict in NA and assured of sales of calculators in that market. This then created another conflict in other nations where multiplication by juxtaposition was taught. Several manufacturers have subsequently switched back to applying multiplication by juxtaposition. And then we have online calculators which also disagree with each other.
This is a case of educators trying to make life easier for students and then breaking mathematics using arithmetic rules.
In my mind Arithmetic is a mechanical calculation to arrive at a single evaluated number, or the 'answer'. Mathematics goes way beyond Arithmetic and is more involved in solving problems through the application of logic.
Another reason North America caught the PEMDAS bug is that America loves multiple choice tests. It allows educators to grade students using automation and is focused on students getting the right 'answer'. I was always graded in school mostly on my method and I would only lose a small amount of my final grade if the answer I arrived at was "wrong' due to a calculation mistake. Showing your method was a requirement to get a passing grade. In the US that has largely been lost in grade schools. I believe this is why Americans that have been taught PEMDAS and have been graded on their ability to get the right answer argue for the strict application of PEMDAS rather than look at the problem mathematically. Adding parentheses to "encapsulate" multiplication by juxtaposition would make mathematical formulas harder to read and write (by hand) and certainly make solving mathematical problems burdensome. Mathematicians are less interested in the minutia of evaluation and focus on the problem at hand.
In my mind logic should prevail insead of being a slave to arithmetic rules that may have limitations.
Don
what happens when you replace 2 with -(1+2) or 5! or 2 arc tangent 60 degrees?
Does Right to left still dominate?
Harold
Exactly. The more sophisticated and algebraically consistent implied multiplication should be standard. Just think about what should be the logical result when one divides collections or variables with units: distance/time = 100 km / 2 hours = 50 km/hour.
Mike
The reason this problem seems 'ambiguous' to people is because they lack understanding of the Order of Operations. Division and multiplication are the same and should be performed in the same step, from left to right. Subtraction and addition are the same and should be performed at the same step.
Note that when I say 'division and multiplication are the same,' I am saying that you can rewrite all division as multiplying by the reciprocal. The division happens to anything directly after the division sign. If there are no parentheses grouping the denominator (like a fraction bar naturally does), then only the first thing after the division sign is divided. Implied multiplication shouldn't take any more precedence than 'regular' multiplication that is shown. Also, when I say 'subtraction and addition are the same,' I am saying that subtraction can be rewritten as adding the opposite.
The order of operations in this problem is as follows:
Work inside parentheses (1+2=3).
Divide 6 by 2 (3).
Multiply 3 by 3 to get 9.
Any perceived 'ambiguity' is from a substandard understanding of the Order of Operations and/or understanding of division/multiplication features. This article suggests that someone jotting down 1/3x means 1/(3x) which is flat out untrue. Jotting that down while intending it to be 1/(3x) shows you don't understand how the Order of Operations ACTUALLY works.
Jon Cherney
Order of Operations is not math. It is a convention, a linguistic agreement between a writer and a reader as to how to decode a written series of symbols into mathematical concepts. Ambiguity occurs when decoders disagree on the method of decoding. If I type 10-6×2 using common western numerals and mathematical symbols, people would come up with the answer of 8. However if I were evaluating 10-6×2 as transliteration of a mahgreb arabic math expression the correct answer would be 2. This is because mahgreb Arabs do order of operations from right to left. (Follow the order of their writing) if they had intended the answer to be 8, they would have written it as 2×6-10. Doing math left to right is just a made up rule devised by Eurocentric left to right readers. It is a convention, not a rule of math. Interpreting a/bc to mean either (a/b)×c or a/(b×c) do not break "rules of math" they just define two similar but distinct decoding interpretations Using one decoding method to attempt to disprove the other is simply circular reasoning. All you need to understand is that there are calculators that use one and calculators that use other. Textbooks and journals that use both and millions of people that USE alternate interpretations to decode math expressions. None answer is universally "right" or "wrong" it is "correctly decoded" or "incorrectly decoded" according to the convention you chose to use. If your purpose is to clearly communicate your intent to your reader, write your expression with sufficient parentheses so everyone, using either convention will correctly interpret your intent.
jack
the dogmatism around the PEMDAS paradox is amazing - I shouldn't waste time on it, but it's a kind of mindless leisure - I ultimately found the APS submission guidelines, published by the American Physical Society, which address precisely the PEMDAS paradox, while never once mentioning PEMDAS, BODMAS, nor any other MASS, fitting expression considering the near-religious fervor of many proponents of these mnemonic devices
https://journals.aps.org/authors/bracketing-mathematical-expressions-h9…
the salient point: [...] "Use enough bracketing to make the meaning clear and unambiguous. Be especially clear with fractions formed with the solidus (/). According to accepted convention, all factors appearing to the right of a solidus are to be construed as belonging in the denominator" [...]
Johnmanjaybee
The real answer to these "problems" posted on social media is "I don't care. I just want to stir up controversy and argument to create lots of comments on my post earning me increased $$$ value to my account." As long as people keep arguing this question, posters keep earning more money.
Pete Palmere
PEMDAS may be a good mechanism for teaching grade school students but it has serious drawbacks especially when moving on to more complex expressions. One teacher, Jason Taff at the Burroughs School in St. Louis points out some of the shortcomings of the mnemonic and has come up with a method for teaching the order of operations based on identifying terms and factors (mathematics Teacher, Vol III, No 2, Oct 2017). Let me quote from that article, "PEMDAS fares poorly because it never was an order of operations to begin with. It has always been a hierarchy of operations. PEMDA tells us what comes first or second or third, when the more relevant concept involves which operations more closely bind numbers and expressions into their nested structure..." So here is where the real foundational differences appear between the sides with those seeing implied multiplication and juxtaposition of variables as more closely binding than explicit multiplication. The one proponents see the sub-expression 2(1+2) as a product in itself with a unique value as if it was surrounded by another set of grouping symbols. Why is this? Let's examine a few areas where grouping is implied though not shown overtly. Take for example the expression 8÷2^3 (8 divided by 2 cubed). One could not simply write as a step to calculate this 8÷2*2*2 since PEMDAS (using the strict left-to-right convention) would evaluate this as 16. So, the indicated exponentiation has to be enclosed in parentheses. Also, take 6÷3! (6 divided by 3 factorial). Again, one could not simply write 6÷3*2*1 as PEMDAS would solve this incorrectly. So, again, parentheses are implied. Now, let's talk about juxtaposition and implied multiplication. My college text, written by a Ph.D. Professor, clearly states that a÷bc is a÷(bc) or a over bc but not (a÷b)*c. For one thing, bc should be seen as a product before division takes place since we are allowed to use commutation and the associative properties of multiplication (in this case variables) to move things around so that bc=cb, and substituting this in the expression would result in different PEEMDAS solutions. that is problematic. Also, what about implied multiplication especially when it comes to factored expressions? Do we now just forget about the distributive property? After all, one could make the case that 2(1+2) is just the factored form of (2+4). Or in its expanded form, (2*1+2*2) using distribution. In each case, the viral expression would resolve to 1. Yes, not every expression showing implied multiplication is a factored version of some group, but even if not, do they not have a unique value in that the multiplier outside the group is the coefficient of that group (or in some cases as factoring also is a GCF). Further, many assert that the P in PEMDAS simply means doing the operation in the grouping. So, in the sub-expression, 2(1+2) they simply add (1+2) and assert that the group is resolved. One could take issue with that especially if it is a factored expression and the GCF is essential in computing the original value of the expression. One could go on about simplifying expressions especially when variables are involved, but let's leave things here and hopefully get some enlightening comments.
Doug
6÷2(1+2) is a simple, well formed, unambiguous problem of division, a÷b, where a=6 and b= 2(1+2), which simplifies to 6. 6÷6=1
Question of notation: axb=ab, and/or any other character, for example c. If we want to show the factors of c, we write (axb).
Factor out the a from (axb) and we get a(b). Thus, ab=c=(axb)=a(b).
a(b) is not interchangeable with a x b, because a(b) represents a product, (a SINGLE number) while a x b is an expression, that is, TWO numbers connected by an operator. However, if we enclose axb in (), it becomes interchangeable with a(b).
Illustration: If 6÷6=1, and 6=2x3, does 6÷6 = 6÷2x3 or 6÷(2x3)????
Easy Rule: Whenever switching from Implicit to Explicit multiplication, ALWAYS enclose the factors involved in ().
Finally, remember that different calculators work differently. Read the instructions, and adjust input accordingly. We should be able to get the same answer on any and all calculators, every time, all the time. If we don't, the problem is probably with our input, not the calculator.
Daniel
I agree completely. Mathematical notation is the written language of maths, so resolving the ambiguity is a language problem, not a mathematical problem.
The division and multiplication symbols are rarely seen in higher mathematics where we tend to use 'algebraic notation', as opposed to 'number sentences' as my teacher wife would call them. This ambiguity arises most often when the two notational forms are used together, either deliberately to provoke discussion on social media, or because it's easier to type inline.
In 'algebraic notation' we treat terms like 'ab' and '6x' as single terms that have already been operated on, so they stay intact. Division is generally represented with a division bar (fraction form) and the grouping of terms above and below the bar makes the order of operations clear. If you choose to use a slash (/) in place of a division bar so it can be typed, then you should add parentheses to indicate the grouping that would have been visually apparent when written with a bar.
Dee
2x = [x + x]
So the statement "2x divided by 2x" is:
[ x + x ] ÷ [ x + x ]
...which, given that x is not zero, has a quotient of 1.
Let's say that in the statement "2x divided by 2x" the value of x is 3
Now the statement is:
[ 3 + 3 ] ÷ [ 3 + 3 ]
Inside each set of brackets, it's "3 + 3" on each side of the division sign, making the statement "6 divided by 6."
A monomial is a single term with ONE VALUE -- which is the PRODUCT of the coefficient multiplied by the variable (factor). With that understanding, a monomial never needs parentheses around it -- it's as if it already has parentheses around it, in much the same way an exponent attached to a base number never needs to be encased inside a set of parentheses. In both cases, you're told how many times to multiply a quantity.
The division sign (obelus), the slash (solidus), and the fraction bar (vinculum) all mean "divided by" -- they are synonymous. Therefore, those division symbols are interchangeable. If you do an internet search for "How to divide one monomial by another monomial," you will find example after example being worked through as a top-and-bottom vertical fraction, even if the division statement was originally written horizontally with an obelus or slash.
The statement "6 ÷ 2(1+2)," the numerator "6" can be factored out as: 2(1+2) ...making the statement: 2(1+2) ÷ 2(1+2) and if we replace what's inside the parentheses with the variable "x," the statement is:
2x ÷ 2x
which can also be written as the horizontal fraction...
2x / 2x
or as the vertical fraction...
2x
__
2x
...since all of those symbols mean "divided by."
The statement "6 ÷ 2(1+2)" is dividing one monomial by another monomial -- it's "2x divided by 2x." Because a monomial is a SINGLE TERM with a SINGLE VALUE, the coefficient cannot just be "peeled off" & used in some other operation as if it had no bearing on the variable (factor).
2x is equal to: (x + x), Therefore, the "2" in "2x" is not a stand-alone number unto itself -- it's the coefficient in a monomial which tells you how many times to multiply the factor (which is actually adding the factor to itself), in much the same way that an exponent tells you how many times to multiply the base number by itself. Just as the exponent is "attached" to the base number, the coefficient of a monomial is "attached" to the variable (factor). So the monomial division statement "2x divided by 2x" is: [ x + x ] ÷ [ x + x ]
Notice that the coefficient number of 2 "disappears" when the statement is written out in its most basic form (as the indicated additions). That proves, once and for all, that using the coefficient of the monomial (the "2" in "2x") in some other operation is not valid.
Division is fractions. Fractions is division. We all know how to work through a fraction: Do all the operations indicated in the numerator, then do all the operations indicated in the denominator, and finally divide the numerator by the denominator.
PEMDAS is incorrect for "processing" division statements.
Dee
According to Study.com:
"Monomials are the product of a coefficient, and a variable or variables."
from Cue Math teaching website:
"Practice Questions on Dividing Monomials"
"Q.1. Divide. 15a^2b^3 ÷ 5b"
The correct answer is listed as: 3a^2b^2
That means that even though an obelus was used to indicate "divided by," the statement was treated as a top-and-bottom vertical fraction, with 15a^2b^3 as the numerator & 5b as the denominator -- with NO PARENTHESES anywhere in the statement.
The "2" in "2x" is not a stand-alone number -- it's the coefficient in a monomial which tells you how many times to multiply a quantity (which is actually adding the quantity to itself), in much the same way that an exponent tells you how many times to multiply the base number by itself. Just as the exponent is "attached" to the base number, the coefficient of a monomial is "attached" to the variable (factor). Thus, the monomial division statement "2x divided by 2x" is: [ x + x ] ÷ [ x + x ]. Notice that the coefficient "disappears" when the statement is written out in its most basic form (as the indicated additions of the quantity). That proves, once and for all, that "peeling off" the coefficient of the monomial (the "2" in "2x") & using it in some other operation is not valid.
In the statement "6 ÷ 2(1+2)," the numerator "6" can be factored out as: "2(1+2)," making the statement:
2(1+2) ÷ 2(1+2)
Replacing what's inside the parentheses with the variable "x," the monomial division is:
2x ÷ 2x
If x equals 3 [expressed as (1+2) ], then the statement "2x ÷ 2x" can also be written as: "6 ÷ 2(1+2)," which is 6 divided by 6 -- which has a quotient of 1.
Division is fractions. Fractions is division. Do all the operations indicated in the numerator, then do all the operations indicated in the denominator, and finally divide the numerator by the denominator. Division has to go LAST. PEMDAS is incorrect for division statements -- because they're fractions.
Mike Stickles
That line from the second paragraph of the article has been well-supported by the comments.
It would be nice if we had an unambiguous order of precedence for operations. Instead, we don't even have an unambiguous list of operations if we can't agree on whether 2(1+2) in the original equation is the same as 2 x (1+2).
I was taught explicitly in school that implicit multiplication was evaluated before explicit multiplication and division. Meaning the answer to the original question is definitely 1, and so 9 is the wrong answer - in my high school math classes. For my kids' math classes, the 'correct' answer would have varied depending on which kid's classes you were looking at.
My only quibble with the author's statement is to note that the question may indeed be well-defined IF you have explicitly defined ahead of time what rules of precedence you're using. Otherwise, it's like asking whether a 17-year-old can legally buy an alcoholic beverage without knowing what country you're in.
Dee
Example:
I own a diner, and just as the breakfast special is about to end, 2 different groups of a dozen people each, walk in & are seated at separate tables. All of those customers order eggs. I look in the restaurant’s refrigerator & see that I have 4 dozen eggs left. If each customer receives an equal number of eggs, how many eggs does each customer get?
4 dozen eggs divided by 2 dozen customers
4 dozen ÷ 2 dozen
(or written with a slash as: 4 dozen / 2 dozen)
Numerically, the statement is:
4(12) ÷ 2(12)
…or…
4(9+3) ÷ 2(9+3)
…which is the monomial division of…
4x ÷ 2x
…when x=12 or x= (9+3).
I deliberately chose to use the word “dozen” because we are all accustomed to buying eggs in that “unit,” which is a box of 12 eggs. It’s easy to understand that when there are 4 full standard packages of eggs, there are 48 eggs in all. That mental image of “4 dozen eggs,” highlights the reason that the coefficient of 4 cannot be separated from its factor of “dozen.” Since multiplication is just a fast way of doing addition, the value of the term “4 dozen” is actually…
1 dozen + 1 dozen + 1 dozen + 1 dozen
...and 2 dozen is actually...
1 dozen + 1 dozen
Also, everyone can easily picture two individual groups of a dozen people, with each group seated as a “unit” of 12 customers at two separate tables in a restaurant, understanding that there are 24 total customers now seated in the restaurant, who are all ordering eggs for breakfast.
The use of “dozen” makes it easy to understand that…
4 dozen divided by 2 dozen = 2
…which can be numerically calculated as…
4(12) / 2(12) =
48 / 24 = 2
…or calculated by canceling out the like factor of “dozen,” which leaves the statement as…
4 / 2
…which, of course, also equals 2.
And if the word “dozen” is replaced with a variable such as “x,” then the statement is…
4x / 2x
…which is one monomial being divided by another monomial, with x=(12) or x=(9+3).
Implied multiplication by juxtaposition indicates that a term is a monomial, such as 4x or 2x (one term with a coefficient & a variable) — never needing parentheses around it, any more than “4 dozen” needs to be completely encased in a set of parentheses to be understood as one term with a single value. Therefore, the “4” in the term “4 dozen,” or the “2” in the term “2 dozen” cannot be detached and used in some other operation in the statement before calculating the total value of the monomial, first. It's the same with monomials like "4x" or "2x," when x=12-- the coefficient can't be "peeled off" and used in some other operation in the statement.
In the monomial division statement 6 ÷ 2(1+2), "6" can be factored out as 2(1+2), making the statement:
2(1+2) ÷ 2(1+2)
Replacing what is inside the parentheses with the variable "x" the statement is:
2x ÷ 2x
...and that monomial division yields a quotient of 1.
Jim Inverness
The Problem with PEMDAS: Why Calculators Disagree
https://www.youtube.com/watch?v=4x-BcYCiKCk
Just to add to the video, From 9:00 you can read what CASIO wrote to her, and here is most of it transcribed:
CASIO describe their PEJMDAS as:
" take following process about calculations because they said that it is natural to calculate inside parenthesis and multiplication with abbreviated multiplicative mark right before parenthesis as top priority, after that to calculate the divisions at the both side:
6÷2(1+2)
=6÷6
=1
"Since 2005 we have launched our calculator fx-ES series to the market ... we adopted an idea supported mainly in North America. They say it is natural to calculate a formula with abbreviated multiplicative sign just the same as a formula without multiplicative one. Based on our hearing result at that moment and under the calculation process below:
6÷2(1+2)
=6÷2x3=3x3
=9
"After launching out calculator FX-ES PLUS series, such as fx-95SG PLUS ... since 2008, our calculator returned to the same specification on the calculation order in a formula as the unit like FX-570MS, base on latest hearing result; we adopted the way of thinking to calculate inside parenthesis and multiplication with abbreviated multiplication sign right before parenthesis as top priority, after that to calculate the divisions at the both side. And this way of thinking is to be kept using as a specification at Casio future calculator products, such as fx scientific series."
Anonymous
There is no way to get 1 legitimately.
First, the article mentions that you can use the distributive property to get 1 by simplifying the expression to 6/(2(2)+2(1)). This is not allowed as the distributive property must distribute the entire term i.e. (6/2) not just the 2 which will give you an answer of 9.
Second, the definition of a(b) is (a x b). There is no debate on this. Taking 6/2(3) can be rewritten as 6/2*3. If one were to evaluate 2(3) first, this breaks the rules of order of operations.
I want to point out that graphing functions present issues with shorthand as shown in the article. Shorthand for graphing software is not well unified and can be interpreted differently as several various companies have created their algorithm to handle these issues, leading to a discrepancy. As the author said, just use parentheses to emphasize what you mean.
Katyakitka
saying The Order of Operations is Intererior of Parenthesis; Exponents; Multiplication and Division whichever comes First leftvto right and then Addition and Subtraction left to right is incomplete.
First it is the Order of Operations between Terms. We have dropped the part "Between Terms" over the years in our obsession to oversimplify or use less syllables.
So the first question is what is a "Term" in mathematics. A term is any single rotated fraction, whole number, number with decimal, or variable (or mathematical symbol of a known value like π or i. A term is also the product of any 2 terms adjacent to each other when at least one is a variable as in 2N. Or AB. A term also includes a parenthetical expression with any term immediately adjective to it. As in a(b+c) or 2(2+N) or in 2(1+3)
We can further see the implications of implied multiplication resulting in a single term when we see a problem like 3N. We understand that 3N is a single term that cannot be solved until we know the value of the variable.
We can learn the value of N if we have one of the following: a value of N listed as 6÷3N= where N = 3-1 so it becomes 6÷3(3-1)= ; or we can solve for N if we already know the equation's total as in 6÷3N=1 or 6÷3N=4.
In the later in 6÷3N=4 to solve for N we would Need to Isolate "N" on one side of the equation. So first step would be to Multiply both sides of the equation so we would get
6 ÷ 3N × 3N = 4 × 3N
The two teams of 3N cancel out on the left side and we now get
6 = 4 × 3N at this point we simplify the right side to get
6 = 12N.
Now divided both sides by 12 and we get
6÷12 = 12N÷12. This time the two 12 cancel out on right side leaving the sole N and we get
½ or 0.5 = N
Now let's look at the 6÷3N= when N=3-1 . First we need to plug in the value for N into the equation. There are 2 ways. We can solve it first or put it in it's spot and then solve.
Either way we need to properly plug it in. Well whether we use 2 or the 3-1 if we don't use parenthesis we would end up with 6÷32 or 6÷33-1. These are both wrong. The value of the parenthesis stays inside parenthesis, but why? Because in 3N the 3 is known as a Coefficient or a factor of N . 3N is like saying (N+N+N) or (3N) But we take the 3 out of the parenthesis for easier equating. So now it looks like 3N or 3(N) when it's outside like this, it is because we have 3 SETS of data or 3 groups of the parenthesis.
So I. 6÷3(3-1) it is literally saying Six divided by 3 Sets of... .
The confusion is when teachers say ÷ and / are the same and ×, *, and ( ) are the same. Not true. When there is only one TERM on either side of the operator / so we have 6/3 and no other operations or terms then yes. It's the same. But is it a fraction or a data set? This question is very important later in more advanced sciences as data sets are maintained as much as possible.
So in 6÷3(3-1) the parenthesis or data set must remain. It's the difference of saying I have 6 fruit and I will divided it but the contents of 3 rooms which each have 3 women and 1 man. Vs saying I have 6 fruit and I will divide it by 3 rooms and then multiply that result by the total of 3 women and 1 man. One will get you 1 fruit per person the other will tell say you need 12 fruit per person. An easier way to write this would be what happens if you put a self identifier of 1 in front of the parenthesis as in 1(3-1). Do you write it as 6÷3(1(3-1)) or 6÷3×1(3-1) or is it 6÷31(3-1)? We all know that the 6÷31(3-1) is incorrect as we cannot change the terms. And just adding the 1 after the 3 changes the term of 3 to 31 (thirty-one) .
But something you also cannot do is add an operation to an equation.
In 6÷3((3-1)/2), -- just to make this easier to observe. -- we can re-write this so easier to see. Aaron 6÷3(½(3-1)) now is that the same? Due to juxtaposition it is. Then according to the idea that / and ÷ Are the same and ( ), ×,* are the same . Then we should get 6÷3(1/2(3-1)) = 6÷3×1÷2×3= 3.
But in the original 6÷3((3-1)/2) we get
6÷3(2÷2) or
6÷3×1= 2. But this should be the same answer why isn't it?
Because implied multiplication takes priority.
Remember that 1 identity addition to (3-1) so it becomes 1(3-1) that can only be done if there is no other term immediately adjacent.
Anytime you see the pattern a(b+c) or a(b-c) they will become (ab+ac) or (ab-ac) respectively. But in 6÷a(b+c) we get 6÷(ab+ac) not ((6b)/a)+((6c)/a).
Now a history lesson. In the late 1980s to early 1990s we had a revolution in home computer access.
With that came Excel. Excel required, due to software programming memory restraints. The earliest computers did not have a way to type an "÷" (obelus) nor a way to type a single fraction like ⅔ with a horizontal bar that was common in text books. They also could not recognize an x as multiplication due to it being a font. So / and * became used.
In the early Excel 6÷3(3-1) would need to be entered as 6/(3*(3-1)). While ÷ and / became somewhat interchangeable the * and ( ) wre not.
Over the next few years Excel began programming ( ) and to be interchangeable but also still required fractions to be ser off by ( ) so seeing 6÷⅗×5(3+2)= you would enter 6/(3/5)*5(3+2).
At the same time teachers had already begun allowing certain brand calculators to be used in schools as a tool. Casio and Texas Instruments (TI) brands were almost exclusively the only ones. Originally both scientific and graphing calculators were programmed with implied multiplication priority. Casio still does. But in 1994 TI introduced a TI-83 which gave implied and explicit multiplication the same and equal priority.
This confused many elementary teachers, many of whom only had general education degrees and not degrees in Mathematics. They.asked TI to pick one method. They chose to not listen, but rather gave instructions in their earlier calculators. Today TI has their answer listed on their Soltuions pages; specifically Texas Instruments Solution 11773. On the page, TI explicitly say IMPLIED MULTIPLICATION has priority so when you type equation as they are written you will get the proper answer. But some of their calculators are written without implied multiplication priority and require an extra set of Parenthesis. For example if you saw 1/2X in a textbook you would type it as is in TI-81, TI-82, and TI-85 family calculators. But in a TI-83, TI-84 Plus, or TI-92 you would need to type it as 1/(2X) to get the proper answer.
Now lets run proofs of 6÷3(3-1)=
If you are of the persuasion of ÷ and / are the same; ×,*, ( ) are the same, and PEDMAS does not give priority to Implied Multiplication you would say 6÷3(3-1)=4
So let's run 2 proofs of answer using a variable in the expression of the equation equal to 4.
Proof a) (compared with the original)
3N÷3N = vs. 6÷3(3-1)
In 3N÷3N as long as N is NOT 0 the answer is 1. Because as we stated earlier 3N is a single term and in mathematics a single term divided by itself is 1.
So we know 3N÷3N=1 and we will compare with 6÷3(3-1)=4
If N = (3-1) we will get
3(3-1)÷3(3-1) = 1. And 6÷3(2)=4
3(2)÷3(2)= 1 (as nothing has changed but solved the interior of the parenthesis.
Next we get
6÷3(2)=1. Again vs 6÷3(2)=4.
If both 3N÷3N=1 and we get to 6÷3(2)=1 when N was equal to 3-1 then how is it when
3N÷3N=1 and 6÷3(3-1)=4 both get to
6÷3(2) one answer is still 1 but the other is 4 only one can be correct.
So now lets look at proof #2.
Since the 2 possible answers are still 1 and 4 lets compare by setting the 3 inside the Parenthesis as a variable to both.
6÷3(N-1)=2. Vs. 6÷3(N-1)=4 and see which gives us N=3
6 ÷ 3(N-1) = 1. Vs. 6 ÷ 3(N-1) = 4
=>
6 ÷ (3N-3) =1. Vs. 6 ÷ (3N-3) = 4
=>
6 ÷ (3N-3) × (3N-3) = 1 × (3N-3) vs. 6 ÷ (3N-3) × (3N-3) = 4 × (3N-3)
=>
6 = 1 × (3N-3) vs 6 = 4 × (3N-3)
=>
6 = 3N-3. Vs 6 = 12N - 12
=>
6 + 3 = 3N -3 + 3 vs 6 + 12 = 12N - 12 + 12
=>
9 = 3N. Vs 18=12N
=>
9 ÷ 3 =3N ÷ 3. Vs 18 ÷ 12 = 12N ÷ 12
=>
3=N. Vs 1.5 = N
So the N im the Equation equal to 1 returns 3 for N while the equation set to equal 4 returned 1.5 for N.
Therefore, since N in 6÷3(N-1)=1 is in the place of 3 in 6÷3(3+1)= is also 1. Not 4.
Please stop teaching / and ÷ Are the same, and stop teaching ×,*,( ) are the same. They are not. You may use them as the same in simple equation of 3(3-1) alone or 3/6 alone, but wjen an equation is expressed with multiple operators they remain unique with their own grammar.
Yes, Math has Grammar.
Dev R.
Leibniz’s Law/Substitution Property of Equality dictates that identical values can be substituted for one another: When z=8, 8=z; when x=2, 2=x; when y=4, 4=y. That’s because the equals sign goes in both directions. On that basis, 8÷2(4)=z÷xy.
Given:
z=8
x=2
y=4
z÷xy
Substituting in numbers for letters, one step at a time:
8÷xy
8÷2y
8÷2(4)
I am certain that every algebra textbook and teaching website on the planet instructs students that a term such as xy or 2y is one term (a monomial), holding the value of the product of its factors. In this case, xy=2(4) and 2y=2(4). So xy=8 and 2y=8.
See teaching website links for definitions and examples of how to divide by a monomial:
https://www.algebra-class.com/monomial.html
https://thirdspacelearning.com/gcse-maths/algebra/simplifying-expressions/
https://www.siyavula.com/read/za/mathematics/grade-8/algebraic-expressions-part-2/08-algebraic-expressions-part-2-02
So…
8÷xy
Calculate the value of xy:
xy=2(4)
xy=8
…making 8÷xy…
8÷8=1
The Substitution Property of Equality is a mathematical law, whereas PEMDAS is just an elementary school highly simplified convention to give kids a “running start” to learn to deal with mixed operations in the same expression. There are no elementary school textbooks I have ever seen which specifically demonstrate for students how to deal with implied multiplication after a division sign (obelus). I have no doubt, however, that there are a myriad of algebra textbooks which demonstrate for students how to divide one single term by another single term, using an obelus in the original expression (even if the term to the right of the obelus has multiple components that are “held together” by implied multiplication, acting as implied parentheses).
Additionally, on a number of tutoring websites (mirroring what is taught in the classroom), algebra students are explicitly instructed to "Rewrite as a fraction," when an expression is originally written with an obelus, with the numerator being the term to the left of the obelus and the denominator being the entire term to the right of the obelus (not just the monomial's coefficient).
It seems that the "strict PEMDAS" crowd forgot that mathematical substitution applies in both directions of an equals sign (from letters to numbers AND from numbers to letters and back again, an infinite number of times).
Dev R.
Hello Dr. Linkletter,
Here's something to consider in your analysis for how to calculate 6÷2(1+2): Leibniz's Law/Substitution Property of Equality, which dictates that substitution cannot change the truth value of a term or an expression. Also, the equals sign is bidirectional, so when a=b, b also equals a.
Additionally, a monomial is defined as one inseparable term holding a single value which is the product of its factors. Thus, xy and 2y are each a monomial.
Therefore, when x=2 and y=3, 2=x and 3=y. In that case, xy=2(3), so 2(3)=xy, as well as 2y=2(3) and 2(3)=2y. In both cases [xy & 2y], the monomial has a combined total value of 6 (via implied multiplication by juxtaposition, which is how a monomial if formed).
Replacing the values of x and y into the term xy cannot change the truth value of the monomial term, thus, xy=2(3) and 2(3)=6, making xy÷xy=6÷6=1, which is identical to 2y÷2y, with 2y=2(3)=6, so xy=6 and likewise, 2y=6.
With all of that being the case with Leibniz's Law and the definition of a monomial, all of the following equalities are true, in sequential substitutions when x=2 and y=3:
xy÷xy=
2y÷xy=
2(3)÷xy=
6÷xy=
6÷2y=
6÷2(3)=
6÷6=1
No math textbook tells students that parentheses are required around a monomial such as xy or 2y. In fact on a number of teaching websites, the phrase "implied parentheses" is used to instruct students on how to interpret and calculate a monomial's value and how to handle a monomial in a division expression.
See teaching websites links below for definitions and solved examples for how to divide by a monomial, including instructing students to "Rewrite as a fraction," when the original expression was written using an obelus:
https://www.siyavula.com/read/za/mathematics/grade-8/algebraic-expressions-part-2/08-algebraic-expressions-part-2-02
"Worked example 8.2 Dividing Algebraic Monomials" tells students to "Rewrite as a fraction."
https://openstax.org/books/algebra-1/pages/6-3-1-dividing-by-monomials
"Look at the division expression -56a^6b^3÷9a^4b^2
"1. Rewrite the division expression as a fraction."
and from Mathway's calculator Algebra Examples:
https://www.mathway.com/popular-problems/Algebra/1012959
Input:
2x÷2x
[Steps]
Rewrite the division as a fraction:
2x
-------
2x
~ ~ ~ ~ ~ ~
Those examples perfectly illustrate that Division=Fraction (so Fraction=Division), thus Obelus=Fraction Bar and vice versa. Since those operational symbols are interchangeable with one another, the obelus and fraction bar share the identical grouping property: Everything above the fraction bar (sans parentheses) is the numerator/dividend and everything below the fraction bar is the denominator/divisor, just as everything to the left of the division symbol is the numerator/dividend and everything to the right of the division symbol is the denominator/divisor.
If that doesn't seem correct to you, take a piece of paper and write the improper fraction of forty-eight twenty-fourths as a top-and bottom fraction, and then write it horizontally using a slash (which is interchangeable with the obelus). Now rotate the paper 90 degrees counterclockwise. Aren't they identical, with the fraction bar slightly angled, only with the numbers 48 and 24 just facing a different direction?
xy÷xy is dividing the product of x & y by the product of x & y, which, when x=2 and y=3, equals 6÷6=1. Any other calculation method would violate Leibniz's Law/Substitution Property of Equality by changing the value of the monomial xy [or 2y] to the right of the obelus, when those are identical terms: xy=xy and 2y=2y, even with an operational sign between them. Thus, the substituted values for xy [and 2y] must still retain its monomial identity as a single term holding the combined total value of the product of its factors.
Isn't this irrefutable proof that some calculators produce an erroneous answer because the programmer failed to take into account Leibniz's Law/Substitution Property of Equality and the definition of a monomial (and how to divided by a monomial)?