Maths in a minute: The fundamental group
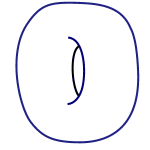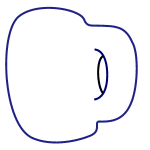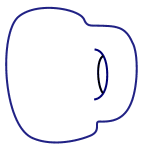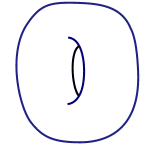
A doughnut mug
In the field of topology two shapes are considered the same if one can be deformed into the other without tearing or cutting. An example are a coffee cup and a donut, as you can see on the right. In other words, topology doesn't care about exact measurements of quantities like lengths, angles and areas. Instead, it looks only at the overall shape of an object, considering two objects to be the same as long as you can morph one into the other without breaking it. But how do you work with such a slippery concept?
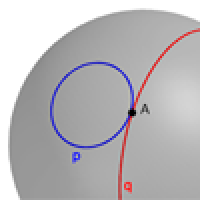
One useful tool is what's called the fundamental group of a shape. Take the sphere as an example. Pick a point A on the sphere and consider all the paths you can trace out on the sphere which start and end at your point A. We will call such paths loops. You consider two loops to be equivalent if you can morph one into the other without cutting either of them. You can combine two loops p and q to get a third one by simply going around p first and then going around q. Also, if you traverse a loop in the clockwise direction, then this movement has an opposite, or an inverse, which is traversing it in the counterclockwise direction.
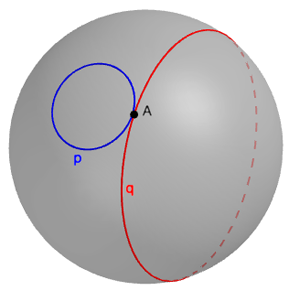
A sphere with two loops passing through a common point.
These two properties, that two loops can be combined to get a third and that every loop has an inverse (together with a couple of other properties), mean that the set of loops (where you consider two loops as equivalent if the can be morphed into one another) form a neat and self-contained structure called a group. It turns out that as long as your object is path-connected (there's a path linking any two points on it) this structure is the same no matter which point A you used as the base for your loops.
Now on the sphere every loop can be transformed into every other loop. In particular, every loop can be contracted into the trivial loop, which goes nowhere and is just your base point A. The fundamental group in this case is also trivial, in other words it contains just one loop. This is true not only for the perfectly round sphere, but also for a deflated football, and for any other 2D surface that's topologically the same as the sphere.
But now think of the surface of a doughnut, also called a torus. In this case not all loops can be contracted to a point because they may wind around the hole of the torus and also around its body.
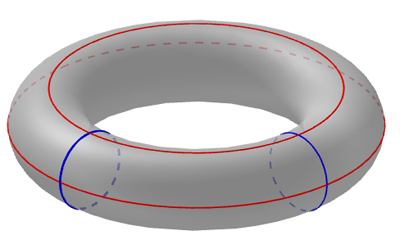
The two red loops wind around the body of the torus and the two blue ones wind around the hole. While the red loops are equivalent to each other and the blue loops are equivalent to each other, a red loop is not equivalent to a blue loop because the two can't be morphed into each other without cutting.
A general loop may wind around the hole a total of m times and around the body a total of n times. It turns out that any two loops are equivalent if they wind around the hole the same number of times and also wind around the body the same number of times. The fundamental group of the torus has the same structure as a group you get from looking at ordered pairs of whole numbers (to be precise, the fundamental group of the torus is isomorphic to direct product ZxZ, where Z is the set of whole numbers). This is true not only for a perfectly round torus, but also for a really irregular and lumpy one. So the direct product of ZxZ, which is a well-understood structure, gives a good characterisation of tori, regardless of their exact geometry.
The concept of fundamental group is a powerful tool in topology, where you can't use precise measurements to describe an object. It's also connected to one of the trickiest problems of modern maths: the Poincaré conjecture. It seems obvious that any object with a trivial fundamental group is topologically the same as the sphere: a trivial fundamental group means that the object has no holes for the loops to wind around and if there are no holes, then the object can always be deformed into a perfect sphere. At the beginning of the twentieth century Henri Poincaré asked whether a similar statement was true for the 3D sphere (which is hard for us to visualise) and found the problem was a lot trickier. It took around 100 years to prove that the answer is yes.
Read more about the Poincaré conjecture, about topology in general and about groups on Plus.
About this article
This article now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Anonymous
Thank you very much