
101 uses of a quadratic equation
It isn't often that a mathematical equation makes the national press, far less popular radio, or most astonishingly of all, is the subject of a debate in the UK parliament. However, in 2003 the good old quadratic equation, which we all learned about in school, was all of those things.
Where we begin

Where would it all end? Was the quadratic equation really dead? Did anyone care? Are mathematicians really evil monsters who only want to inflict quadratic equations on a younger generation as a means of corrupting their immortal souls?
Maybe so, but it's not really the quadratic equation's fault. In fact, the quadratic equation has played a pivotal part in not only the whole of human civilisation as we know it, but in the possible detection of other alien civilisations and even such vital modern activities as watching satellite television. What else, apart from the nature of divine revelation, could be considered to have had such an impact on life as we know it? Indeed, in a very real sense, quadratic equations can save your life.
The Babylonians
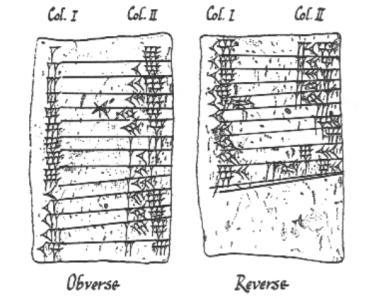
Babylonian cuneiform tablets recording the 9 times tables
Let's suppose that you are a Babylonian farmer. Somewhere on your farm you have a {\em square} field on which you grow some crop. What amount of your crop can you grow on the field? Double the length of each side of the field and you find that you can grow {\em four} times as much of the crop as before. The reason for this is that the amount of the crop that you can grow is proportional to the {\em area} of the field, which is in turn proportional to the {\em square} of the length of the side. In mathematical terms, if $x$ is the length of the side of the field, $m$ is the amount of crop you can grow on a square field of sidelength 1, and $c$ is the amount of crop that you can grow, then $$c = m x^2.$$ This is our first quadratic equation, naked and blinking in the sunlight. Quadratic equations and areas are linked together like brothers and sisters in the same family. However, at the moment we don't have to solve anything - until the tax man arrives, that is! Cheerily he says to the farmer "I want you to give me $c$ crops to pay for the taxes on your farm." The farmer now has a dilemma: how big a field does he need to grow that amount of crop? We can answer this question easily, in fact $$x = \sqrt{ \frac{c}{m} }.$$
Finding square roots by using a calculator is easy for us, but was more of a problem for the Babylonians. In fact they developed a method of successive approximation to the answer which is identical to the algorithm (called the Newton-Raphson method) used by modern computers to solve much harder problems than quadratic equations.
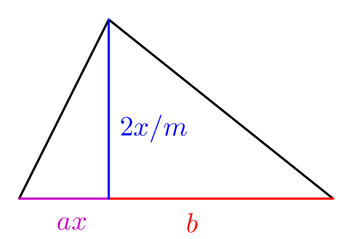
For appropriate values of $a$ and $b$ the amount of crop that the farmer can grow in this field is given by $$c = a x^2 + b x.$$ This looks a lot more like the quadratic equation that we are used to, and even under the evil eye of the tax man, it's a lot harder to solve. Yet the Babylonians came up with the answer again. First we divide by $a$ to give $$x^2 + \frac{b}{a} x = \frac{c}{a}.$$ Now we {\em complete the square} by using the fact that $$\left( x + \frac{b}{2a} \right)^2 = x^2 + \frac{b}{a} x + \frac{b^2}{4a^2}.$$ Combining this with the original equation we have $$\left( x + \frac{b}{2a} \right)^2 = \frac{c}{a} + \frac{b^2}{4a^2}.$$ This is now an equation that we can solve by taking square roots. The result is the famous "$-b$ formula": \[ x = -\frac{b}{2a} \pm \sqrt{\frac{c}{a} + \frac{b^2}{4a^2}}, \] which can be rewritten as \[ x = \frac{-b \pm \sqrt{b^2 + 4ac}}{2a}. \] (The formula usually has "-4ac" because the quadratic equation is more usually written in the form "$ax^2+bx+c=0$".) \par The fact that taking a square root can give a positive or a negative answer leads to the remarkable result that a quadratic equation has {\em two} solutions. So much for mathematical puzzles only having one solution! \par Now, this is where the teaching of quadratic equations often stops. We have reached that object beloved of all journalists when they interview mathematicians - a {\em formula}. Endless questions can be made up which involve putting values of $a,b$ and $c$ into the formula to give (two) answers. But this isn't what mathematics is about at all. Finding a formula is only the first step on a long road. We have to ask, what does the formula {\em mean}; what does it tell us about the universe; does having a formula really matter? Let's now see where this formula will take us.
A surprise for the Greeks, a bit of mathematical origami and a sense of proportion
We now fastforward 1000 years to the Ancient Greeks and see what they made of quadratic equations. The Greeks were superb mathematicians and discovered much of the mathematics we still use today. One of the equations they were interested in solving was the (simple) quadratic equation $$x^2 = 2.$$
They knew that this equation had a solution. In fact it is the length of the hypotenuse of a right angled triangle which had sides of length one.
It follows from Pythagoras' theorem that if a right-angled triangle has shorter sides $a$ and $b$ and hypotenuse $c$ then $$a^2 + b^2 = c^2.$$ Putting $a=b=1$ and $x = c$ then $x^2 = 2$. Thus $x = \sqrt{2}.$ \par So, what is $x$ in this case? Or, to ask the question that the Greeks asked, what {\em sort} of number is it? The reason that this mattered lay in the Greek's sense of {\em proportion}. They believed that all numbers were in proportion with each other. To be precise, this meant that all numbers were {\em fractions} of the form $a/b$ where $a$ and $b$ are {\em whole numbers}. Numbers like 1/2, 3/4 and 355/113 are all examples of fractions. It was natural to expect that $\sqrt{2}$ was also a fraction. The huge surprise was that it isn't. In fact $$\sqrt{2} = 1.4142135623730950488 \ldots ,$$ where the dots $\ldots$ mean that the decimal expansion of $\sqrt{2}$ continues to infinity without any discernible pattern. (We will meet this situation again later when we learn about chaos.) \par $\sqrt{2}$ was the first {\em irrational number} (that is, a number which is not a fraction, or rational), to be recognised as such. Other examples include $\sqrt{3}$,$\pi$, $e$ and in fact "most" numbers. It took until the 19th century before we had a good way of thinking about these numbers. The discovery that $\sqrt{2}$ was not a rational number caused both great excitement (100 oxen were sacrificed as a result) and great shock, with the discoverer having to commit suicide. (Let this be an awful warning to the mathematically keen!) At this point the Greeks gave up algebra and turned to geometry. \par Far from being an obscure number, we meet $\sqrt{2}$ regularly: whenever we use a piece of A4 paper. In Europe, paper sizes are measured in A sizes, with A0 being the largest with an area of $1 m^2$. The A sizes have a special relationship between them. If we now do a bit of origami, taking a sheet of A1 paper and then folding it in half (along its longest side), we get A2 paper. Folding it in half again gives A3, and again gives A4 etc. However, the paper is designed so that the proportions of each of the A sizes is the same - that is, each piece of paper has the same shape.
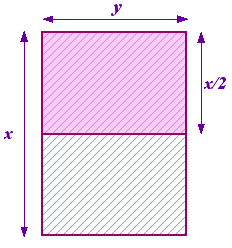
The proportions of the first piece of paper are $x/y$ and those of the second are $y/(x/2)$ or $2y/x$. We want these two proportions to be equal. This means that $$\frac{x}{y} = \frac{2y}{x},$$ or $$\left( \frac{x}{y} \right)^2 = 2.$$ Another quadratic equation! Fortunately it's one we have already met. Solving it we find that $$\frac{x}{y} = \sqrt{2}.$$ This result is easy for you to check. Just take a sheet of A4 (or A3 or A5) paper and measure the sides. We can also work out the size of each sheet. The {\em area} $A$ of a piece of A0 paper is given by $$A = xy = x \left( \frac{x}{\sqrt{2}} \right) = \frac{x^2}{\sqrt{2}}.$$ But we know that $A=1 m^2$ so we have another quadratic equation for the longest side $x$ of A0, given by $$x^2 = \sqrt{2} m^2 \quad \mbox{or} \quad x = \sqrt{\sqrt{2}} m = 1.189207115 \ldots m.$$ This means that the longest side of A$2$ is given by $x/2 = 59.46 cm$ (why?) and that of A$4$ by $x/4 = 29.7cm.$. Check these on your own sheets of paper.
Paper used in the United States, called foolscap, has a different proportion. To see why, we return to the Greeks and another quadratic equation. Having caused such grief, the quadratic equation redeems itself in the search for the perfect proportions: a search that continues today in the design of film sets, and can be seen in many aspects of nature.
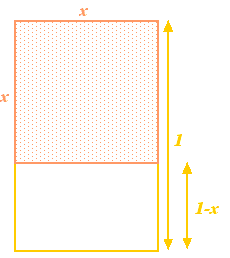
Let's start with a rectangle, and then remove a square from it with the same side length as the shortest side of the rectangle. If the longest side of the rectangle has length 1 and the shortest side has length $x$, then the square has sides of length $x$. Removing it from the rectangle gives a smaller rectangle with longest side $x$ and smallest side $1-x$. So far, so abstract. However, the Greeks believed that the rectangle which had the most aesthetic proportions (the so called Golden Rectangle) was that for which the large and the small rectangles constructed above have the same proportions. For this to be possible we must have $$\frac{x}{1} = \frac{1-x}{x} \quad \mbox{or} \quad x^2 + x = 1.$$ \par This is yet another {\em quadratic equation}: a very important one that comes up in all sort of applications. It has the (positive) solution $$x = \frac{\sqrt{5}-1}{2} = 0.61803 \ldots.$$ The number $x$ is called the {\em golden ratio} and is often denoted by the Greek letter $\phi$.

 Sunflower seeds, arranged using Fibonacci numbers |
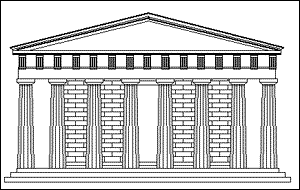 The Parthenon, embodying the Golden Ratio |
In this sequence each term is the sum of the previous two terms. Fibonacci discovered it in the 15th century in an attempt to predict the future population of rabbits. If you take the ratio of each term to the one after it, you get the sequence of numbers \[ \frac{1}{1}, \frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}, \frac{8}{13},\ldots \quad\mbox{or}\quad 1, 0.5, 0.66667, 0.6, 0.625, 0.61538, \ldots \] and these numbers get closer and closer to (you guessed it) the Golden Ratio $\phi$. \par By finding both of the roots of the above quadratic equation we can actually find a formula for the nth term in the Fibonacci sequence. If $F_n$ is the $n$th such number with $F_0 = 1$ and $F_1 = 1$ then $F_n$ is given by the formula $$ F_n = \frac{(1/\phi)^n + \phi^2 (-\phi)^n }{1 + \phi^2}. $$
Conics link quadratic equations to the stars

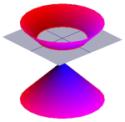
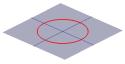
Half of the cone can be visualised as the spread of light coming from a torch. Now, if you shine a torch onto a flat surface such as a wall then you will see various shapes as you move the torch around. These shapes are called {\em conic sections} and are the curves that you obtain if you take a slice through a cone at various different angles. Precisely these curves were studied by the Greeks, and they recognised that there were basically four types of conic section. If you take a horizontal section through the cone then you get a {\em circle}. A section at a small angle to the horizontal gives you an {\em ellipse}. If you take a vertical section then you get a {\em hyperbola} and if you take a section parallel to one side of the cone then you get a {\em parabola}. These curves are illustrated below.
 |
 |
 |
 |
 |
 |
 |
 |
 A cross-section of a cone can be a circle ... |
 ... an ellipse ... |
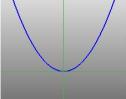 ... a parabola ... |
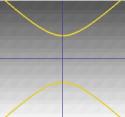 ... or a hyperbola. |
These curves were known and studied since the Greeks, but apart from the circle they did not seem to have any practical application. However, as we shall see in the next issue of Plus, a link between quadratic equations and conics, coupled with a mighty lucky fluke, led to an understanding of the way that the universe worked, and in the 16th century the time came for conics to change the world.
About the authors
Chris Budd is Professor of Applied Mathematics in the Department of Mathematical Sciences at the University of Bath, and the Chair of Mathematics at the Royal Institution in London.
Chris Sangwin is a member of staff in the School of Mathematics and Statistics at the University of Birmingham. He is a Research Fellow in the Learning and Teaching Support Network centre for Mathematics, Statistics, and Operational Research.
They have recently written the popular mathematics book Mathematics Galore!, published by Oxford University Press.
This article was inspired in part by a remarkable debate in the British House of Commons on the subject of quadratic equations. The record of this debate can be found in Hansard, United Kingdom House of Commons, 26 June 2003, Columns 1259-1269, 2003, which is available online at the House of Commons Hansard Debate website.
Comments
Anonymous
What a great shame such concepts are seldom if ever taught in schools framed in historical and application context as they have been in this article.
Anonymous
I agree with you. Children also need to know that a quadratic equation is a way to describe a physical thing, such as the arch of a bridge. I never understood that and no one ever told me that. I figured it out on my own when, as an adult, I restudied math. If they could see that math is a descriptive language that we all make use of, whether we fully realize it or not, they would then A) more readily understand math, and B) see its worth rather than question its worth.
Anonymous
Just nitpicking here, but wouldn't 3000 B.C. be the Sumerians, not the Babylonians? It's been a while since I took Near Eastern studies, but I'm pretty sure the Babylonians didn't come around until mid third millenium B.C.
Anonymous
Yes you are right, they weren't around yet.
Anonymous
The information regarding quadratic formulas has helped me visualize and clearly grasp the concept for potential applications. Amazing!!
I am one who has struggled in the subject yet determined to understand it.
Anonymous
Hey,
I really like your website. For the first time ever, I see the importance of the quadratic formula. However, I need some help with a step, using the triangular field to develop c = ax^2 + bx. Why is the height 2x for the two right triangles. It's probably easy, but it's a step that is mysterious to me and my long work day, tired brain.
Thanks!
Anonymous
Great article, wonderful introduction to quadratic equations.
I had exactly the same difficulty - and after over 50 years my school maths is really, really rusty.
There must be a good reason as to why they chose those particular ways of denoting base and height of the triangle (rather than just b and h), and I assume it is correct. Still do not really understand that bit.
However if you use those expressions in the area formula for a triangle (area = half base time height) then it does come out.
JonnyM
I could follow through up to the triangular field example. I suspect that there is some factoring and cancelling going on.
Nevertheless, I found this article useful in explaining WHY we have quadratic equations, and knowing why we have them helps me understand why/where/how we might apply them in real life situations. This was never taught to me at school. Instead, we just had to recognise when an equation was quadratic, learn the formula, then apply it.
Gregory D. MELLOTT
Yes, the formula that follows now makes sense. The height of the perpendicular now makes sense where it is "2x", and not "2x/m".
Anonymous
Wonderful article!!!!!!!!!
Anonymous
I enjoyed this article very much. The combination of history, that I love, with algebra, that I struggle with, made my understanding of the concepts of functions easier. I especially appreciated seeing the conics sections and the application of each into graph equations. You all gave me an "aaha" moment. Keep up the good work. Debra
Anonymous
I learned to factor quadratics in first grade. They're tame. I learned how functions can model "anything" when i watched the standard deviants algebra videos.
More generalized polynomials can be a pain to factor, though.
Anonymous
Well, you must have been the smartest first grader in the world, I can't even figure this out in the 8th grade.
Anonymous
It must have been a great effort to bring out these significance of quadratic equations. Immensely impressed. Appreciate the good job..
Anonymous
the research done on quadratic equation is awesome i always found it boooooring but this what is written is simply great.
the Babylonians and the Greeks are awesome i really loved reading it and hence forth in 11std i would surely do it thoroughly.thank you very much authors
Anonymous
I always said that had no meaning at all, and why learn it if I won't ever use it again. This article has completely shut me up. I enjoyed every bit of this arcticle, very interesting introduction on Quadratic Equations. The information providded on quadratics had seriously helped me understand it a lot more. Its amazing how they use physical things such as the bridge and the arch to solve the dimensions.
Anonymous
This helped me understand the relevance of the quadratic equation. Incorporating the history of mathematics demonstrates how mathematics helps people become more efficient to finding solutions to world problems. Many students shut down mentally and emotionally when it comes to mathematics. in the United States. I'm trying to find ways to help change the way we instruct in the United States.
Anonymous
I don't think that I ever had a math instructor that actually knew the subject until I reached college. It was a true joy to ask questions and get real answers. The US is crippled in math and science because k-12 education has become a union racket to employ the otherwise useless. The best way to change the way we instruct is to abolish all state funded public schools, disband public unions that kick back campaign money to the supposed representatives and let the parents and local school boards freely fire the worthless drones.
Kytriya
Actually, the reason why we can't get good math teachers is becuase the industry hires them at a much higher rate of pay then what the schools can pay. We get the "left overs" to choose from. I lucked out, and happened to get 3 very good math teachers. But I was the exception, and clearly not the rule.
Anonymous
This has definitely helped me understand quadratic equations. This is a subject that I have previously struggles with an after reading this article, I can understand it much better. I enjoyed learning about the history of quadratic equations and reading the explanations. Great article and very well put out!
Anonymous
Part of the Quadratic Equation Article states:
"which is in turn proportional to the square of the length of the side. In mathematical terms, if (x) is the length of the side of the field, (m) is the amount of crop you can grow on a square field of side length 1, and (c) is the amount of crop that you can grow, then"
"m" and "c" sound like the same thing? Is this a typo?
Marianne
The two are different: m is the amount you can grow on a field of unit side length and c the amount you can grow on the field under consideration (side length x).
Anonymous
Please expand on how you derived the labels on the Triangle and how then they fulfill the equation c = ax^2 + bx.
Anonymous
"At this point the Greeks gave up algebra and turned to geometry."
Honestly? So did I! I am an artist, I think graphically. Geometry, Geography, Cartography, Orthography, etc. have always come to me easily. Irrational Quadratic Equations (IQE), as taught in most public schools in the United States of America, make absolutely no sense, and serve no discernible purpose in the real world.
My own instructors dedicated 50% or more of their courses to IQE, frustrating me to no end, because they wouldn't move on to anything else once they reached them. They constantly asked on written assignments to merely, "Solve.", equations. Then they always complained about the result I wrote, even when it was correct, because they wanted me to, "Show my work."
The process of going through the formula was more important to them than the result. None of them understood that I used a different means to get to the result, that was faster, and just as accurate. I didn't understand why they insisted upon writing mathematical expressions that were needlessly complex to denote an equation that was effectively upside down, backwards, and turned inside out. For them, algebraic notation was a mathematical puzzle to be taken apart and put back together, providing 'proof' that the expression was true at all points in the progression.
I skipped the algebraic notation and went directly to the result. I didn't need 'proof', I just wanted to get the work done. I knew in my heart that no one would actually write equations of the sort they expressed when attempting to solve real world issues in an expedited manner.
This article is very well written. I wish I had come across something of this sort thirty years ago, when it could have done me some good. Instead, it wasn't until I took classes in Trigonometry that it all fell into place. Trigonometry did for me, as an artist, what Algebra did for my high school instructors. Trigonometry acted as a mathematical bridge between Arithmetic, Geometry and Algebra, that I could traverse at will.
Unta Glebin Gloutin Globin
Red Ronin, The Cybernetic Samurai
Anonymous
I think it is nearly impossible that the Babylonians thought there were 360 days in a year. I think you are implying that the number of degrees in a circle were chosen because the earth moves through almost one degree of its orbit each day. It's more likely that they chose 360 degrees as an outgrowth of their love for the number 60 - because it has so many factors. If you choose 60 for the internal angle of an equilateral triangle you get 360 degrees in a circle.
Anonymous
The radius of a circle will fit inside the circle six times exactly to form a hexagon; the corners of the hexagon each touch the circumference of the circle. Babylonians did indeed have a love for the number 60 and if each of the sides of the hexagon are divided into 60 and a line drawn from each 60th to the centre of the circle then there are 360 divisions in the circle.
Anonymous
Thanks for going to the trouble of explaining the history and applications of quadratic equations. The point of it all was never explained to me when I was thrown into the deep end with them, age 10. Now that I've been asked to explain them to a friend's son, your material is helping to demystify things. Matt, North Wales, UK
Anonymous
I can't get beyond c = a x^2 + b x. How is this equation derived from the figure given? There's no explanation as to what "a" and "b" actually represent?
Anonymous
I was wondering the same thing. In the diagram I take ax to be the base of the smaller triangle but then where is x in the equation coming from? Are a and x equal?
Anonymous
I'm also stuck on that 1st example of the field comprising 2 triangles and how we get to the quadratic equation from that. I would love to go through the rest of this article but don't want to until I've overcome the hurdle of understanding this. Please, someone?
Marianne
The area of the smaller of the two triangles is ax^2/m and the area of the larger one is bx/m (from the standard formula for the area of triangles). This means that the area of the whole field is ax^2/m+bx/m. Since the amount of crop that can be grown on a field of unit area is m, the amount of crop that can be grown on a field of area ax^2/m+bx/m is m(ax^2/m+bx/m) = ax^2+bx.
Terry Bernstein
But why is the base of one triangle ax and of the other simply b. Where does that ax value come from?
Manny
can someone please explain terrys question-why is one base ax and the other one simply b. also why is the height 2x/m. where does the m come from.
Terry Bernstein
I can understand Anon's frustration back in Jan '16. So often in mathematical explanations I've read I find myself tripping over a missing step. Like a mathematical pothole. It's usually something so obvious to the mathematician who wrote it that it didn't seem to need mentioning. ( Like where that little square came from- though I did eventually work that one out). The problem is that if you are trying to follow a set of mathematical steps even if you solve the missing one (as with me and the small square) you have been diverted away from the main problem and lost the thread: And then probably give up and go off and do something else instead.
Sir Derp
It's just a quadratic equation in standard form tweaked ie ax^2 + bx + c vs c = ax^2 + bx and if a is anything other than 1, then you remove it, etc~
Mr.B
I'm pretty sure when they sought out ways to derive a quadratic equation to help them reason triangular regions they had to think frontwards and backwards. First, I believe you need to understand how the height 2x/m came into play (why it was used). First, keep in mind that "m" represents a basic unit of 1. That would mean that 2x/m (the height for BOTH triangles would appear to be 2x. But are their heights 2x? Let's think about it, when finding the area of a right triangle we eventually divide the area by 2 after multiplying the b x the h. Knowing this, it is mathematically reasonable why the coefficient of "2" was put in front of x-it would get divided back out and preserve what they really wanted for the height of the triangle/ length of one side of the land "x". This mean that the small triangular area would be ax times x or (ax^2). The larger triangular area would be b times x or bx for its area. You asked though "what is "a" and "b"? look at length of base "a", compared to the triangles height that we previously deduced to really be "x". "a" represents a coefficient thats taking a fraction of base length "x" for the small base is being represented in terms of the height of the triangle or length of the land. Base b ls obviously the second width of the scalene triangle or width of land that IF represented with bx instead of b (like it is) would have created a bx^2 term instead of the bx we need to figure out the area the land in addition to other things. This is my perception after being confused there for a minute too. I hope this helped you or someone just a little although it's years later- just discovered this awesome forum:).
Will
I really can't follow what you're saying. I just want to know where that expression for the height comes from. So I called it h to get the total area of the triangle as h(ax+b)/2. Total total yield of this area will be hm(ax + b)/2.
So I can appreciate that ax must be something relating that smaller triangle to the height, and if I set h = x, I get m(ax^2 + bx)/2 for the total yield. Substituting h = 2x/m gives ax^2 + bx which is the area of two quadrilaterals with the same height of x and 2 sides of ax and b. So the yield, which should be a product of area and the coefficient m is now rendered as the areas of two squares without having anything to do with that coefficient anymore. Taking the height to be x again and the bases as they are, the total yield for the aggregate quadrilateral is m(ax^2 + bx), and for the triangles would be that over 2. Rearranging gives ax^2 + bx = 2yield /m. So if the yield of the quadrilateral (divided by m) of height x is ax^2 + bx, then the height at which the yeild of the triangles is equal to that is 2x/m. I can see all that but I just can't grasp what on earth is going on and its doing my head in
Anonymous
Sir, the Babylonians were not in power in 3000 BCE, it was the Sumerians. Babylonians took over Mesopotamia at around 1900 BCE.
Ming
Please provide a link to the next issue continue this topics on conics and quandraic.
nidhi
Great!!!! what an explanation.. really we need a teacher who teaches basics like this in the beginning to all children
elfatih
Thanks so much I kept getting my anwsers wrong because I didn't realize you had to divide both parts by the denominato
Mike Jones
“The reason that we teach symbolic algebraic manipulation has everything to do with its efficiency and nothing to do with the historical development of the problems being solved.”
-- Patricia R. Allaire and Robert E. Bradley (in their article ‘Geometric Approaches to Quadratic Equations from Other Times and Places’, available online at: https://www.maa.org/sites/default/files/images/upload_library/46/NCTM/G…)
Maria
I noticed a few people were confused about the choice of height for the triangle, so here is my explanation :)
m is the amount of crops that you can grow in 1 square unit of area.
c = mx*x is the amount of crops you can grow in a square field of length x.
So, c = m*Area of Square
For triangle, c = m* Area of Triangle = m (base*height)/2
Base = ax*x + b*x
Choose height = 2x/m so that:
c = m (ax*x + b)*(2x/m)/2
the m on the numerator is divided by m on the denominator to give 1, and 2/2 also gives 1
So, height = 2x/m means that the m "cancels out" and so does the 2 to give the desired quadratic formula:
c = ax*x + b*x
Hope this helps.
Math Destruction
Thanks for your comment, it has been helpful.
But I would like to know why did they use (2x/m) as its height? And I would like to break that question into two
1) having ax on the small triangle's base implies that there's a relationship with the base and it's height. What is the relationship? Isn't it two separate events?
2) Similar question to "m" how does the "m" in the height have any relation with the "m" that's being used for amount of crops that can grow in a sqft.
Because if the height was replaced with a "y", the whole formula wouldn't exist eventho it may or may not equals to 2b/m.
Maria
Oooops. Typo. My previous explanation should have "ax" not "ax*x" :)
Maria
Oh dear. The "b*x" should be just a "b".
Way past my bedtime :)
Mirjana Bozic
Esteemed Budd and Sungwin, Your collection of examples of the use of the quadratic equation is Excellent. My congratulations to you for this collection. We found it while writing our article “Visualizing Properties of a Quadratic Function Using Torricelli’s Fountain” which was published in The Physics Teacher. We cited your collection in our article. Mirjana Božić