
What computers can't do
Alan Turing is described by Professor P.N. Furbank, overall editor of Turing's Collected Works[1], as "one of the leading figures of twentieth-century science".

Figure 1: Alan Turing.
Sixty years ago his most famous paper was published, introducing the idea of a Universal Computing Machine ten years before the first stored programme digital computer actually ran.
This was only one of a string of varied achievements. It is known now that his work on deciphering the German Enigma code at Bletchley Park during the Second World War made a significant contribution to winning that war, though this remained unknown to his closest friends until after his tragic death from taking potassium cyanide in 1954.

Figure 2a: The Enigma machine. (Image source : [ http://agn-www.informatik.uni-hamburg.de/ ] AGN, University of Hamburg, Copyright 1995, Morton Swimmer).
Turing's wartime work played a significant role in marking out the importance of mechanical computing facilities. Although much of the hack work was done mechanically, an enormous team of human computers was also involved.

Figure 2b: Close-up of the coding rotors.
Another feature of his wartime work was its use of probability theory. Some of Turing's work in this area was also highly innovative. It was recognised after the war through the published work of his then assistant (later Professor) Jack Good, without reference to its wartime uses.
Turing's interest in computing continued after the war, when he worked at NPL (National Physical Laboratory) on the development of a stored-programme computer (the ACE or Automatic Computing Engine). In 1948 he moved to Manchester, where the first stored programme digital computer actually ran that year.
Although his connection with that real computer was at best tenuous, he made significant contributions to computing theory, in particular artificial intelligence (the Turing test), computer architecture (the ACE) and software engineering. It is some measure of his contribution that the prestigious Turing Prize in computing science is named after him.

In the Turing test for machine intelligence, an observer has to distinguish between the machine and a human by asking a series of questions through a computer link.
The halting problem
As an example of his thought let's look at a proof that there is no way of telling in general once a computer has embarked on a calculation whether that calculation will terminate in an answer. This problem is known as the "Halting Problem for Turing machines" and was first proved in the 1937 paper[2] in which he introduced his machines.
To lead up to that proof, it is necessary to say a few things about counting and lists or sequences. We say that the elements of a set can be counted if they can be listed in a single sequence.
The set of natural numbers can be listed 0, 1, 2, 3,... and so on ad infinitum - no problem. To list all the integers, positive and negative in a single sequence, you can write 0, 1, -1, 2, -2, 3, -3,... and so on, again no problem.
The fractions take a bit more work. It is usual to do this in 2D, using a table or matrix. Let's just look at the positive ones - it extends to include the negative ones as with the integers.
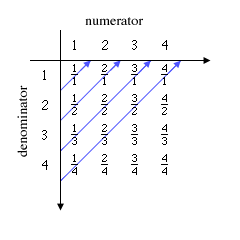
Figure 3: Table of fractions. The fractions can be counted by tabulating them and then counting them along the diagonals, shown in blue.
There are a lot of repetitions - all the diagonal elements are equal for a start - so this algorithm is a little wasteful. But it does the job. Carry it on for ever and every fraction will be there somewhere in the 2D matrix. To write the matrix out in a single sequence, work up and down the SW to NE diagonals to obtain:
1, 1/2, 2, 1/3, 2/2, 3, 1/4, 2/3, 3/2, 4,...
Next, we come to a very famous theorem, Cantor's Theorem, which says that the real numbers are not countable in this way. The set of real numbers include numbers like Pi (3.14159...) which cannot be written as one whole number over another.
Proof of Cantor's Theorem
Let's just show that we cannot count all the binary sequences, in other words, infinite sequences of 0s and 1s.
Suppose we could. We can label each binary sequence B1, B2, B3,... ad infinitum. We will now obtain a contradiction. Let's list the elements of each sequence in a table or matrix as before.
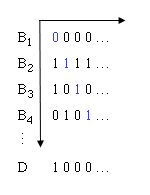
Figure 4: Table of binary sequences. A possible list of binary sequences, the sequence D is constructed by inverting the items on the diagonal, shown in blue.
Now define a binary sequence, D, by choosing a 0 in the first column if B1 has a 1 in that column and 1 if B1 has a 0 in that column. We then choose a 0 in the second column if B2 has a 1 in that column and 1 if it has a 0 and so on. The resulting binary sequence, D, cannot be in the list because if it were it would have to match one of the B sequences, say Bn for some n. But we have just deliberately made sure that the nth column of D differs from Bn. Contradiction.
No matter how we list the binary sequences we can always find a new sequence, D, which is not in the list.
This procedure is called diagonalising. As you can see, we have given a simple rule for it, so that given a rule for counting out a list of binary numbers then we'd have a rule for computing this diagonal binary number which isn't in the list.
Turing's argument
Finally, let's sketch how Turing's argument (related to an even more famous bit of reasoning by Kurt Gödel in 1931) takes this argument a big stage further.
The proof sketched here is not Turing's original one, but related. Much of Turing's classic paper is taken up with describing his concept of a computing machine and why it is as general as can be. Anything that can be computed according to a finite list of rules, can be computed by one of his machines.
Briefly, a Turing machine can be thought of as a black box, which performs a calculation of some kind on an input number. If the calculation reaches a conclusion, or halts then an output number is returned. Otherwise, the machine theoretically just carries on forever. There are an infinite number of Turing machines, as there are an infinite number of calculations that can be done with a finite list of rules.
One of the consequences of Turing's theory is that there is a Universal Turing machine, in other words one which can simulate all possible Turing machines. This means that we can think of the Turing machines as countable and listed T1, T2,... by a Universal Machine through a sort of alphabetical listing. Turing used this to describe his own version of Gödel's Theorem: that there is no mechanical procedure for telling whether a Turing machine will halt on a given input: the Halting Problem.
The unsolvability of the halting problem
Let's represent the result of using the nth Turing machine, Tn on the input i as Tn(i). Suppose that there was a rule or procedure for deciding whether or not Tn(i) halts for all values of n and i.
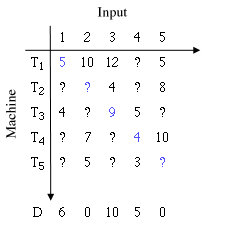
Figure 5: A halting rule could be used to make a table of the output Tn(i), using a question mark to represent calculations which never halt. This table is only illustrative, its contents have not been chosen with any particular ordering of Turing machines in mind.
But then by a similar diagonalising procedure to the one above, we can define a new Turing machine, say D, which will halt for all inputs and return the following output for input i:
- 0 if Ti(i) does not halt.
- Ti(i)+1 if Ti(i) does halt.
But this machine D must be one of those machines, in other words it must be Td for some d. However, we just defined it to give a different answer from Td with input d. Contradiction.
The extra sophistication here over the original diagonalising argument lies in (1) all the listing done is itself computable and (2) any machine Tn may or may not halt in carrying out its computations. None of this enters into Cantor's original diagonal argument. This sort of computable diagonalising was first used in the pioneering work done by Gödel, Turing and others in the decade before the Second World War, and has remained an important technique. The really hard work lies in formulating the various definitions of computability, but that is another story!
What is life?

Figure 6a: Turing's meticulously hand-drawn sunflower.
In the closing years before his death, Turing was working on something entirely different, something which had been close to his heart since his school days - the origin of biological form - Morphogenesis.
Figure 6b: A close-up section.
How could simple cells know how to grow into relatively enormous structured forms? The crucial idea that genetic information could be stored at molecular level had been deduced in Schrödinger's 1943 lecture What is Life?, and Crick and Watson were currently busy in the uncovering of that secret, through the structure of DNA. Given the production of molecules by the genes, Turing was looking for an explanation of how a chemical soup could possibly give rise to a biological pattern.
The first main goal of his theory was an attempt on the classic problem of Phyllotaxis, the arrangement of leaves on a plant. One of the features of this subject which had been known since Kepler's time was the natural occurrence of the Fibonacci series 1, 2, 3, 5, 8, 13, 21,... So it was already established that mathematics had a role to play. (For more about the Fibonacci series see "The life and numbers of Fibonacci" in Issue No 3.)
Turing also proposed that the pattern of markings on animals followed mathematical rules due to chemical signals. This idea had mixed fortunes, though recently biologists' interest has been re-vitalised. Using his theory, researchers in Japan have observed Turing's predicted changes in the patterns on zebra-striped fish.
Further reading
Glance at the web page below for further details of the Collected Works
- The Alan Turing Bibliography, assembled by Andrew Hodges.
The definitive work on his life (a compelling read) is:
- Andrew Hodges, Alan Turing: The Enigma, hardback version - Burnett books, 1983, paperback version - Vintage Books, 1992.
A new angle on Turing can be found in:
- Andrew Hodges, Turing, in the Series The Great Philosophers, Phoenix 1997.
A guiding force from his schooldays was:
- D'Arcy Wentworth Thompson, On growth and Form, Cambridge University Press. 1917 (new edition 1942).
References
[1] Collected Works of A. M. Turing edited by P.N. Furbank, North-Holland, Elsevier Science.
[2] On Computable Numbers, with an application to the Entscheidungsproblem, Proceedings London Mathematical Society (series 2) vol 42, 1936-7, pp.230-265.
The author
Mike Yates is an Emeritus Professor of the University of Manchester, and an Honorary Professor of the University of Wales at Bangor.
Comments
Anne_Carlill
I'm doing a course on algorithms and this article is very useful. However can someone answer this - Is zero a natural number? I thought it wasn't but am now unsure.
Anonymous
There are arguments for and against.
A long time ago it was not considered a natural number.
However it does obey all the normal rules (pretty much) and so it is generally accepted as being natural.
However there is no accepted consensus.
Anonymous
Thanks for this information. The idea of an Oracle computer sounds exciting. Do you think the will ever create an Oracle machine that can overcome the halting problem on another Oracle machine of the same capacity?
Raymond.cavallaro@gmail.com
I guess what you say must be the consensus in math community, but still the math does not feel right for me.
Let’s start with comparing the countable fractions with the uncountable Booleans.
In the countable fractions the axis are both natural numbers, so they have both the same “amount” or “proportion”, that means that by taking a diagonal, you are getting the same “rate”, that seems counter intuitive dealing with infinite but it means that each item on the rows will interact with all the itens in the cols and vice versa.
On the Boolean side if you had a finite amount n in the cols (numbers) you would have a 2^n rows, so taking a diagonal would leave a lot of solutions off the diagonal, if you think in other way, as all Booleans would represent an integer number so you can see that taking all the Booleans is infinite but countable.
So I conclude that the diagonal analysis shows that something is uncountable or there is a difference in the rate of the axis.
In the case of the halting table Tn(i) , I came to understand that the n “amount” or “rate” has more itens than the natural number infinity i, but that is not all, the “halt program” could not be a universal Turing machine unless it could take at least n*i inputs.
but I have no bases for that is just a thought.