Solution to the optimal stopping problem

The probability of choosing the best partner when you look at M-1 out of N potential partners before starting to choose one will depend on M and N. We write P(M,N) to be the probability.

For any value of N, this probability increases as M does, up to a largest value, and then falls again. P(1,N) and P(N,N) will always be 1/N because these two strategies, picking the first or last potential partner respectively, leave you no choice: it's just like picking one at random. Our aim is to find when P(M,N) is largest.

Suppose that you have collected the information from M-1 potential partners and are considering the Kth in sequence.

Since the potential partners come along in a random order, the chance that this one is the best is 1/N. But you only consider this potential partner if the highest ranking potential partner that you've seen so far was among the first M-1 of the K-1 that you have rejected (otherwise you wouldn't be looking at this potential partner at all). This happens with the following probability:

So the overall chance of achieving your aim of finding the best potential partner this time is:

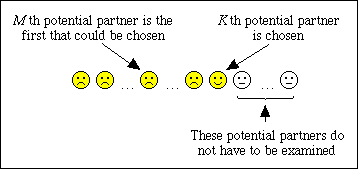
But K can take any of the values in the range from M to N, so we can write:

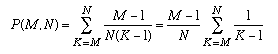
The best value of M will be the one which satisfies:

(If you want to be very awkward, you could ask what happens if there are two "best" values of M, with one of those strict inequality signs replaced by a partial inequality. It turns out that the only time when equality is possible is when N=2, which is not very interesting anyway.)

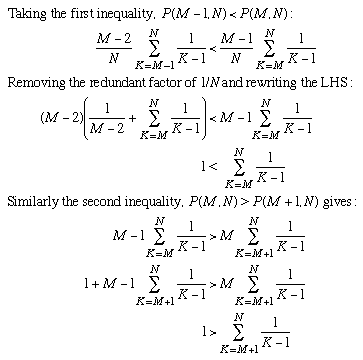
We can use these inequalities to find M for any N. Try it! Fill in the blanks below:

[Answers]

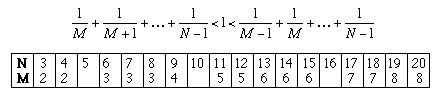
The fraction of the potential partners that you see M/N is tending to a limit as N becomes large. There is a sum in the calculation of P(M,N) which appears in other situations in mathematics too:

Using this equation we can calculate an approximation for P(M,N) as follows:

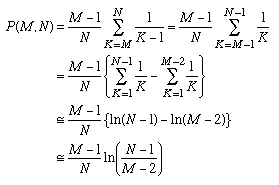
For big N, we can make it even more simple:

In order to find the best value of M we have to apply the approximation to the conditions that we derived before:

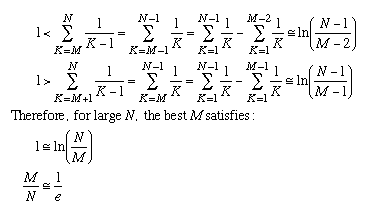
1/e is about 0.368. This result can be expressed simply in the following "37%" rule:

37% rule

Look at a fraction 1/e of the potential partners before making your choice and you'll have a 1/e chance of finding the best one!

Further reading:

For more information see the article "Mathematics, marriage and finding somewhere to eat" elsewhere in this issue.

Answers to problems:

[Back to questions]