
Lost but lovely: The haversine
Sine, cosine, and tangent — we do love our trigonometric functions! So imagine our bliss when we recently came across a function we had never even heard of before. It's called the haversine and it's defined in terms of the sine function:
$$\mbox{haversin}(\theta) = \sin^2(\theta/2).$$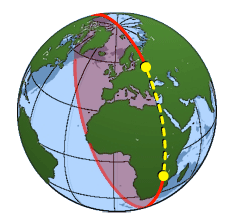
The dotted yellow line is an arc of a great circle. It gives the shortest distance between the two yellow points. Image courtesy USGS.
The term "haversine" apparently comes from "half versed sine". To see why this function is useful, put yourself in the shoes of an intrepid traveller setting out on a sea voyage from Liverpool to New York. The first thing you'd want to know is how far you will have to travel. Ignoring islands, rocks, currents and other inconvenient factors, let's say that you will travel along the shortest path between the two cities. We know that the shortest path between two points is along a straight line, but that fact doesn't help you here. The straight line that connects Liverpool and New York cuts right through the Earth and you are not about to dig a tunnel.
You need the shortest path on the surface of the Earth, which is roughly spherical. On a sphere the shortest path between two points is along an arc of a great circle: that's a circle drawn on the surface of the sphere which is centred on the same point as the sphere and has the same radius. Any two points lie on a unique great circle, which they divide up into two arcs. The shortest path between the points is along the shorter of these two arcs.
So how do you calculate this great circle distance between two points $P$ and $Q$ on the Earth? First, recall that the locations of the two points are given by their latitudes, for which we will write $\phi_P$ and $\phi_Q,$ and their longitudes, which we will denote by $\lambda_P$ and $\lambda_Q.$ Write $R$ for the radius of the Earth, which is roughly $6,371$ km. The great circle distance $d$ between $P$ and $Q$ comes from the formula \begin{equation}\sin^2{\left(\frac{d}{2R}\right)} = \sin^2{\left(\frac{\phi_2-\phi_1}{2}\right)} + \cos{\phi_1}\cos{\phi_2} \sin^2{\left(\frac{\lambda_2-\lambda_1}{2}\right)},\end{equation} (where the angles are measured in radians). Solving for $d$ gives \begin{equation}d = 2R \sin^{-1}{\left(\sqrt{\sin^2{\left(\frac{\phi_2-\phi_1}{2}\right)} + \cos{\phi_1}\cos{\phi_2} \sin^2{\left(\frac{\lambda_2-\lambda_1}{2}\right)}}\right)}.\end{equation} You'll admit that this isn't the simplest of formulae. If you were are a seafarer hundreds of years ago, armed only with sine and cosine tables to help you, working out the distance $d$ would prove pretty cumbersome. There's a square root to take, as well as the inverse of the sine function .... argh! But now let's replace any expressions of the form $\sin^2(\theta/2)$ by the haversine function. Expression (1) above becomes $$\mbox{haversin}\left(\frac{d}{R}\right) = \mbox{haversin}\left(\phi_2-\phi_1\right) + \cos{\phi_1}\cos{\phi_2} \mbox{haversin}\left(\lambda_2-\lambda_1\right).$$ The distance $d$ is now $$d = R \;\; \mbox{haversin}^{-1}\left(\mbox{haversin}\left(\phi_2-\phi_1\right) + \cos{\phi_1}\cos{\phi_2} \mbox{haversin}\left(\lambda_2-\lambda_1\right)\right).$$ Working out the great circle distance between two points is so important in navigation that people in the old days produced tables giving the values of the haversine function and also of the inverse of the haversine function. This made seafarers' lives a lot easier. Working out the distance $d$ only involved looking up two cosine values and two haversine values, adding and multiplying them in the correct way, looking up the inverse of the haversine function and multiplying by $R$— done! The reason why the haversine function has come out of fashion is that with the help of calculators and computers it's easy enough to work out the distance $d$ straight from formula (2). That's why you don't find a haversine button on your average calculator. Let's give it a go. Liverpool has latitude $53.4^\circ$ and longitude $-3^\circ$, and New York has latitude $40.71^\circ$ and longitude $-74^\circ$. These are measured in degrees. Converting them into radians (multiplying by $\pi/180$) gives $\phi_L = 0.932^\circ$ and $\lambda_L=-0.052^\circ$ for Liverpool, and $\phi_{NY} = 0.71^\circ$ and $\lambda_{NY}=-1.291^\circ$ for New York (rounded to three decimal places) Plugging these into expression (2), with the radius of the Earth $R = 6371$, gives a great circle distance of around 5313 km. Quite a way to go!
Örjan Sandström
Actually haversine in navigation is still evolving.
Hanno Ix and Greg Rudzinski reworked an old method of celestial navigation (Doniol) to get a very compact system with few sources of error, it utilizes ONLY haversines to solve the pzx triangle for both computed height
-almost same as great circle distance for stars if you disregard atmospheric refraction, oblatenes of earth and other real world inconveniences-
and azimuth to the projectionbject altitude With only addition, subtraction and one division.
This acievement does not sound like much, but for a lightly seasick sleepdeprived person in the cramped and frequently badly iluminated confines of a small craft it reduces error sources...