The hidden beauty of multiplication tables

Zoheir Barka
Submitted by Marianne on April 7, 2017

In this article we explore some of the symmetries that hide within the multiplication table of positive whole numbers.

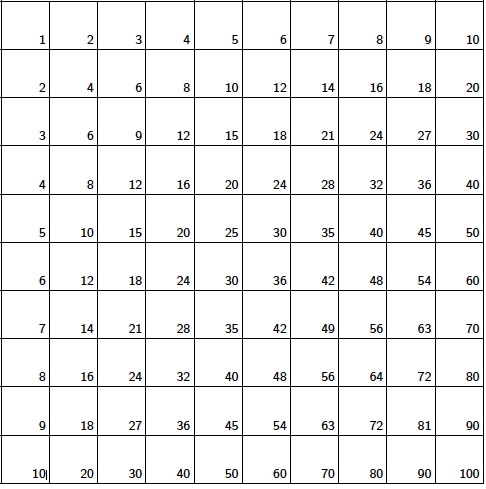
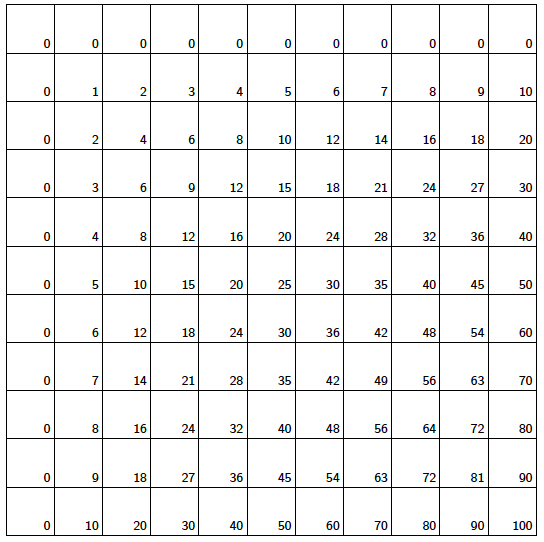
Let us start with the standard multiplication table. The table below contains the numbers 1 to 10 in the first row and the first column. Any other square contains the product of the first number in its row and the first number in its column.

Table 0

We will add a row of $0s$ at the top and a column of $0s$ on the left. This still gives a consistent table — the first row and column contain multiples of $0$,  the second row and column contain multiples of $1$,  the third row and column contain multiples of $2$, etc — and it will provide a nice frame for our patterns.
Table 1

In the following, we will colour the squares of the multiplication table that correspond to multiples of a number $k$ for various values of $k$. And we’ll discover some beautiful symmetries.

Single multiples

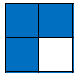
We begin with $k=2$: we assign the colour blue to every square in the multiplication table that is a multiple of $2$. (The number $0$ is a multiple of $2$, so all the $0$ squares are blue.)
Table 2

Here we have extended the table a bit so that it runs until the number 15 in the horizontal direction. Indeed, since the complete multiplication table on positive integers is infinite on two sides, we will continue to tweak the dimensions of the tables in what follows to display the emerging patterns more clearly.

Note that the whole pattern above can be pieced together using the fundamental building block:

Fundamental building block

The fundamental building block contains $k \times k = 2 \times 2 =4$ cells of the multiplication table. The squares defined by the white cells in the pattern consist of

  \[ (k-1)^2=(2-1)^2=1 \]    

cells.

Below are two more images in which the multiples of a number $k$ have been coloured blue. Can you tell what the value of $k$ is in each case? Can you tell what the fundamental building blocks are, how many cells they contain, and how many cells make up the squares defined by the white cells? You can post your answers in the comment field below — in case you can’t work them out, we’ll publish the answers in a few weeks’ time.

Table 3

Table 4

Multiple multiples of consecutive numbers

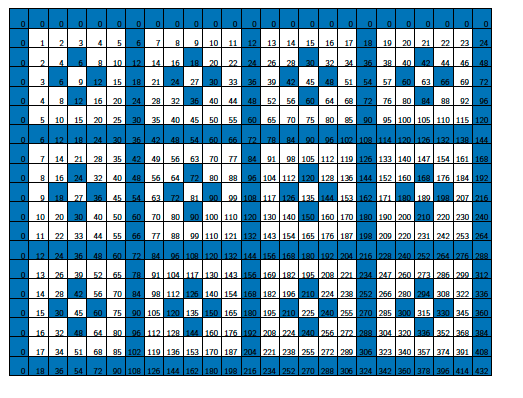
A more interesting pattern emerges if we use multiple multiples, and corresponding to them, multiple colours. In the following figure, the numbers that are multiples of $2$ are coloured red, and those that are multiples of $3$ are coloured orange (with the orange taking precedence over the red in the case of multiples of both $2$ and $3$, that is, multiples of $6$).

This gives the following pattern.

Table 5

Note that this time our fundamental building blocks consist of $ 6 \times 6 = 36$ little squares, which makes sense, because $6$ is the least common multiple of $2$ and $3$. The symmetry emerges from repeated copies of a $5 \times 5$ square with a nice four-fold symmetry.

The next figure takes this a step further, assigning red to numbers that are multiples of $2$, orange to numbers that are multiples of $3$, and yellow to numbers that are multiples of $4$. If a cell is a multiple of two of these numbers (eg $6=2\times 3$) then it will be assigned the colour of the larger of these two numbers (orange in the example). We will stick to this convention for the rest of this article.
Table 6

This time, our fundamental building blocks contain $12 \times  12$ cells, which again makes sense, given that $12 $ is the least common multiple of $2$, $3$ and $4$. The symmetry emerges from repeated copies of an $11\times 11$ square, which contains nine small $3 \times  3$ squares which together create a nice four-fold symmetry.

We can carry on playing this game indefinitely. The next four figures use multiples of four, five, six and seven consecutive numbers respectively, and four, five, six and seven colours respectively. What patterns can you discern? Can you find any axes of (reflectional) symmetry? What should be the size of the fundamental (repeating) building blocks of symmetry in each case? Remember that you can post your answers in the comment field below, and in case you can't work them out, we'll publish the answers in a few weeks' time.

(Click on the images to see a larger version.)

Table 7
Table 8
Table 9
Table 10

Multiples of non-consecutive numbers

Next we use some non-consecutive values of $k$. The following figure uses blue for numbers that are multiples of $6$, and green for numbers that are multiples of $9$.

(Click on the image to see a larger version.)

Table 11

The fundamental building blocks will now consist of $18 \times 18 = 324$ little squares, as $18$ is the least common multiple of $6$ and $9$. Still the additional symmetries within the nine $5 \times 5$ squares that make up the repeated $17 \times 17$ squares may come as pleasant surprises. Can you find mathematical explanations for these?

Here are a few more patterns for you to admire. In each case we colour the multiples of non-consecutive numbers. Can you tell what numbers these are and describe the patterns that emerge? Remember that you can post your answers in the comment field below, and in case you can't work them out, we'll publish the answers in a few weeks' time.

(Click on the images to see a larger version.)

Table 12
Table 13
Table 14
Table 15
Table 16

Remainders

Finally, if we fix a number $k$ and assign colours to cells depending on their remainder with respect to $k$, then all the squares can be filled in. For example, let multiples of $5$ be black, numbers with a remainder $1$ with respect to $5$ be green, numbers with a remainder $2$ with respect to $5$ be red, numbers with a remainder $3$ with respect to $5$ be purple, and numbers with a remainder $4$ with respect to $5$ be yellow; the following figure is obtained.:

(Click on the image to see a larger version.)

Table 17

Conclusion

We've discovered some of the symmetries that hide within the multiplication table of positive integers. It's easy to create these patterns (for example, using Excel) and they can all be explained without much difficulty using the arithmetic of whole numbers and divisibility criteria. Displaying these symmetries using colours introduces a new facet to the maths. These images and others created in similar ways may appeal to students of mathematics and the arts, and may lead to new collaborations. At the very least such images may, we hope, intrigue, amaze, and inspire.

About this article

Zoheir Barka , from Laghouat in Algeria, is an amateur and self-educated mathematician. He has a Masters degree in French language from Laghouat University and is currently a French teacher in elementary school.

A version of this article first appeared as The hidden symmetries of the multiplication table in the Journal of Humanistic Mathematics, Volume 7, Issue 1 (January 2017), pages 189-203.

Comments

Submitted by James S. on April 11, 2017

It should say remainder 4 with respect to 5 be yellow; the following figure is obtained

numbers with a remainder 1with respect to 5 be red; the following figure is obtained.

Submitted by Marianne on April 11, 2017

Thanks for pointing out the mistake, we have corrected it.

Submitted by Raúl A. Simón E... on April 14, 2017

¡Beautiful! Congrats to the author.

Submitted by Oli on April 19, 2017

These are lovely, I wonder if there's any interesting animations to be had as the integers created the patterns are changed? I suspect there are!

Submitted by Barka on April 25, 2017

Hi! you would like to check this link, you will find an interactif tool to display the different modulo's :
http://guzintamath.com/blog/2017/02/modulus-hidden-symmetries/

Submitted by Ken Wessen on June 27, 2017

Thanks for this article. It inspired me to make a web app to explore the patterns - you can find it here: http://thewessens.net/ClassroomApps/Main/multiples.html?topic=number&id=20