
What is a black hole – mathematically?
We asked cosmologist Pau Figueras everything you've ever wanted to know about black holes. In the other part of the interview he explained what black holes are, physically, and how we hope to observe them. In this second part of the interview, he explains how Einstein's theories predict their existence, and how to describe them mathematically.
Please note that since this interview was conducted, hard evidence for black holes has been detected. It comes from gravitational waves. See Black holes exist! to find out more.
How were black holes first predicted?
Einstein published his [general theory of relativity] in late 1915, and only a few months later, in early 1916, [Karl] Schwarzschild found the first solution of the Einstein equations. [By solution we mean some values for the variables describing the curvature of spacetime and the distribution of matter that satisfy the Einstein equations.] [This solution] describes the gravitational field of a spherically-symmetric body: a black hole.
At that time it wasn't understood that that solution corresponded to a black hole. In fact even in the 30s the greatest minds of that time, [including] Einstein himself, despised the idea of a black hole because it contained a singularity, namely a place where curvature is so large that even general relativity breaks down. It took nearly 50 years to really understand what a black hole is, and this was done only in the 1960s.
General relativity asserts that massive objects curve spacetime (see here to find out more). How do black holes affect the curvature of spacetime?
The strength of the gravitational field is measured in terms of the curvature. And because black holes are very massive and they are very small, their gravity is very strong and [creates] a very large curvature of spacetime.One way to characterise the curvature is something called the Schwarzschild radius: $$ R_s = \frac{2 G_N M}{c^2} $$ where $G_N$ is Newton's constant [of gravity], $M$ is mass of the object and $c$ is speed of light.
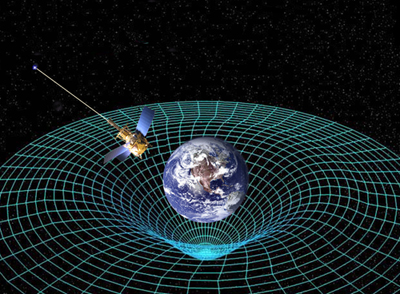
Massive bodies warp spacetime. Image courtesy NASA.
The Schwarzschild radius is, more or less, the size that a given object, with a given mass, should have in order for it to be a black hole. For instance, if we managed to concentrate all the mass of the Earth into a sphere of a radius of a few centimetres, then that object would be a black hole.
Of course we know that this cannot happen because there are other forces in nature which prevent it, but in other circumstances it can happen. For example, when very massive stars run out of nuclear fuel, they cool down and they collapse, and at some point they become small enough so that the whole mass fits within a Schwarzschild radius – therefore they form a black hole.
For example, the Schwarzschild radius of the Sun is of the order of a few kilometres. So if we managed to concentrate the whole mass of the Sun into a sphere of a few kilometres, then that would be a black hole.
Can you characterise a black hole so simply, with just a few features, such as mass and size?
One of the reasons why black holes are so important in our understanding of general relativity is because of their simplicity – because they are made of the most fundamental building blocks of the theory, namely space and time alone. They are very simple and therefore we can understand them.
This [is in contrast to] other gravitational objects, such as stars. In order to understand a star, [as well as needing] to take into account general relativity, you also need to understand nuclear physics to account for the nuclear reactions [and] plasma physics to understand the transport of heat within the star. This gets very complicated and we are often led to study these objects within certain approximations.

Simulated view of a black hole. Image: Alain Riazuelo.
We don't have to do that with black holes because they are only made of space and time, so we have a complete understanding of them within our theory alone. We don't need any other physics. This simplicity gets translated into the fact that they are just described in terms of very few parameters.
In the vacuum case, if the black hole is static, then it must be spherical and there is only one parameter characterising the black hole, namely its mass. [However], objects in nature, like stars, rotate, so the black holes that occur in nature should have some rotation. The Schwarzschild solution was found [just] months after Einstein published his theory, but it took another 50 years to find the general solution which has rotation and is relevant to describe the black holes [we might find in] nature. This Kerr solution is described entirely by just two parameters, namely the mass and the spin of the black hole. With these two parameters you can fully characterise all black holes in nature and we don't need to make any approximations to understand those objects. This is why they are so important.
In a sense, black holes are no different than elementary particles [in particle physics] because we only need to specify a few parameters [to describe these]. The same with black holes - [they] are the elementary particles of general relativity.
Are black holes the biggest open mystery of general relativity?
Yes. Black holes are a prediction of general relativity and we know of several instances in nature where we think that they should occur, but we haven't detected them yet. So it's still an open question whether they [exist] or not, or whether they have the properties that general relativity predicts. [Please note that since this interview evidence for black holes has been discovered. See here.]
This is important because most of the tests [of] general relativity [involve] situations where gravity is weak, or relatively weak. For example, we've tested bending of light, the precession of the perihelion of Mercury.
Detecting black holes would be important because the signals that we would get, namely those gravitational waves, would be generated in regions where gravity is very strong. It would allow us to test the strong field regime of general relativity, which is something that we haven't been able to do so far. This would put very strong tests on general relativity, so it's very important that we [observe] black holes: [the observations would give us] a completely new window into general relativity.
Watch the full interview with Figueras in this video or listen to it as a podcast.
About this article
Pau Figueras is Stephen Hawking advanced postdoctoral research fellow at the University of Cambridge.
Comments
Crag Hunter
I have often though of all singularities being connected to the same place. Could it be that black holes are providing the energy and material for the continued expansion of the universe? Each one a gravitational link to the event horizon of the expanding universe and a their formation a natural consequence of this?
Adam Gazdag
With a force of gravity as strong as that of a black hole, I find it highly unlikely that the singularity would intermingle with others of its kind. Black holes are born from the explosion of massive stars that literally rip a hole in spacetime. By this being said, its become popular opinion that on the other side of the black hole (escaping the 'white hole') is a whole new region of dimensional reality - with new laws of physics and nature.
It'd be a cool thing to see though. This would add to the expanding idea that the universe is a massive sphere. Like the earth, we'd start a one location, set sail, and wind up being able to return back to that location having "sailed" across the surface of the cosmos.
Tina Mcrae
So if we could bend it like Beckham we could create a short cut ?
But is space time an actual thing ?
or is it like the wind it exists, but we can’t see it ?
My mind is getting blown now.
I so much want to understand it. Unfortunately I have no education
but at 64 years of age my interest is still that little girl who at 4
when I first looked through my telescope I absolutely adored the universe.
Is there a book for me to simplify it a wee bit ?
Hope I have not offended all the great minds out there ☺️
8-8008
The universe made up only of motion is created by an absolute static outside of the universe. Example on a small scale is electromagnetism generates from a power plant. The flow of those waves is only possible due to the static of the generator. However, that is not an absolute static as per the definition of it the absolute static has no matter, energy or space or time but creates it.
Richard Fradd
Assuming a black hole rotates about an axis. As more and more matter is absorbed by the black hole and there is no reduction in rotation speed would there come a time when the "equator" approaches the speed of light? Our understanding of forces means that the particles could not exceed the speed of light and the black hole would become less spherical and more shaped like a rugby ball. To extrapolate further there would come a time when the "North and South" of the black hole would emit energy as the particles escape the gravitational field. Like an ice skater spinning when they bring their arms in the rotation speed increases the black holes rotation speed should also increase. This would fuel more particles to be emitted North and South. There is also a case for Hawking radiation at the equator. Opinions please.
Hayden Gebhardt
Hello,
Background: I am a Sophomore at MIT majoring in Electrical Engineering and Physics.
I am having some difficulty understanding where you make some of your connections, however, I believe I understand the general idea. Here are some of my concerns/reservations about your claims:
1. When you add mass to a black hole, it becomes less dense. Think about two planets colliding (m1,m2); the collision would not produce an object with a radius = r1 +r2. The volume of the object may double, but remember that the volume is determined by the cube of the radius rather than the radius itself, thus, the radius only increases by the cube root of two. In terms of black holes, the density is defined by mass/volume, and mathematics has shown that when you double the mass, the volume increases eightfold (2/(1/4)). An interesting connection can be drawn to further clarify: If you have a black hole with a mass that is 387 million times that of our sun, it would have a density roughly that of water.
2. Where my understanding of your claims diverge is when you refer to the equator of the black hole. For this case we will assume that black holes rotate about the same axis that their former stars did. When defining the components of a black hole, we can identify most things with limits involving infinity and zero. A black hole, as you probably know, is comprised of a singularity, where if we define the black hole on an x-y-z plane, is a vertical limit approaching negative infinity on the z-axis. The point theoretically exists at the end of this theoretical, snow-cone-like shape, and is the source of the immense gravitational pull that black holes are so famously known for. Black holes also have what we call a Schwarzschild radius. We define this as a relationship between C and "R," where "R" is the radius of the black hole where the gravitational force is equal and opposite to the speed of light with respect to R(hat). Before that is the event horizon, the umbra shrouding the interior of the black hole (we can see where the event horizon begins because F of gravity is < C). So, when you mention the black hole's "equator," I assume you're referencing the semi-sphere that we can define mathematically as the event horizon. Reduction in rotational speed exists so long as you have a gravitational force, a velocity of your reference object, and a radius to reference. Centripetal acceleration, which would be used in most cases, can be defined as V^2/R where V (in this case) is C and R is anywhere you want it to be in the black hole. R has a finite distance where C becomes < the force of gravity, as referenced previously, and the point I believe you're referencing is the limit approaching the Schwarzschild radius, but you could also be mentioning either side of the radius (from the top or bottom - think hyperbolic). I suppose this is where I'd ask for clarification.
3. Ice-skaters.
When an ice-skater pulls their arms in, they accelerate centripetally because they decrease their overall radius, thus producing a larger "a." This example helped me understand what you were talking about. Visible electromagnetic radiation is emitted from just outside the event horizon of a black hole, which is easily explained since it doesn't have to overcome the immense escape velocity that dwells in the inner boundaries of the black hole, but what you're asking about is Hawking Radiation, which relies on the fact that black holes have a finite entropy - which is still highly theoretical. Hawking Radiation, since it does not obey the properties confined to the electromagnetic spectrum, could theoretically escape from inside the event horizon, allowing your claim to be valid.
4. Here's the rub...
Hawking Radiation is about as soundly developed as quantum mechanics, and I'm in no position to validate or invalidate cutting-edge claims in that field, and neither is anyone at this point, unfortunately.
5. Rugby
Please excuse my trite response, but my answer as far as the polarity and shape of an angularly accelerating black hole is about as extensive as my knowledge on ancient Greek poetry... if you catch my drift, haha. But given the things we know about physics, objects with mass and gravitational pull attract, and black holes aren't magnetic enough to repel each other. When two black holes collide, they form a quasar, which has the same "anatomical shape," if you will, as a normal black hole. It's vector and scalar values diverge, however (density, mass, volume, etc...). At this point, it is hard to discern how a quasar behaves with respect to Hawking Radiation and I apologize that I cannot help you further.
6. Opinions
I've provided my knowledge, now here are my opinions.
1. I really do like the idea you have with reference to the ice-skater, but I don't know that a black hole behaves the same as normal bodies do, because centripetal acceleration does not yield time dilation, and black holes are theorized to slow time as the distance between a chosen photon and the singularity approaches zero (for more info see the theory of Special Relativity - with respect to black holes, of course).
My suggestion to you is to pursue research on quasars, Hawking Radiation, and the physical forces allowed in the domain of a black hole, as I'm sure professors and scholars who are more well-versed that I could help you a bit more.
2. I'm curious as to what your background is in terms of Physics. Knowing this would allow me to know what theories and concepts you are taking into account when forging your theories, which could also help me - maybe you know way more than I do and I need to catch up!
3. Let me know what you've found out since I posted this comment!
CoreyT
As you said. Ice skater.
As the Star collapses on its iron core we have several metals spinning around each other. I would assume this generates an increasingly stronger magnetic field. As the iron starts to fuse into heavier elements might one of them be a rare earth element that increases this magnetism and further increases the pull and further increases fusion of elements into even heavier ones.
On the surface as a interesting thing to me. Could a black hole create some sort of anti matter object in a quantum state that becomes what we see. That they persist for so long because all the antimatter is essentially gone and what little it can generate or accumulate to balance itself is what we see happening. It’s like a computer counting digits in pi but it can’t stop until something changes a digit that causes pi to unbalance and calculate out. Bad example but the equation wants something that’s essentially not in our universe anymore.
davidjonz2005
curvature of light around black hole is due to gravity
what is the reason of breaking light in a lens?