
Suppose that during a given time period an event happens on average $a$ times. For example, you might know that on average you'll see three new posts on your social media feed per minute. This doesn't mean that the event will occur exactly $a$ times during every such time period: sometimes you might see five new posts a minute and sometimes just 1. So you're justified in asking, "what's the probability I will see exactly $k$ new posts in a single minute?" Here $k$ could be 0, or 1, or 2, or any other positive integer.
To answer this question you need a probability distribution — in fact, you need the Poisson distribution. It works as long as the events in question are all independent of each other and says that the probability of seeing the event exactly $k$ times in a unit of time is
$$P(Event=k)=\frac{a^k e^{-a}}{k \times (k-1) \times ... \times 2},$$
where $e=2.71828...$ is Euler's number.
In our social media example, the average $a$ is equal to $3$ posts per minute. Assuming the posts are all independent (so one post doesn't spawn or prevent other posts), the probability that you see exactly one new post in a given minute is therefore $$P(Event=1) = \frac{3^1 e^{-3}}{1} = \frac{3 \times 0.05}{1} = 0.15.$$ The chart below shows the poisson distribution for $a=3$. As $k$ gets larger the probability of seeing $k$ events per unit time tends to zero, as you'd expect.
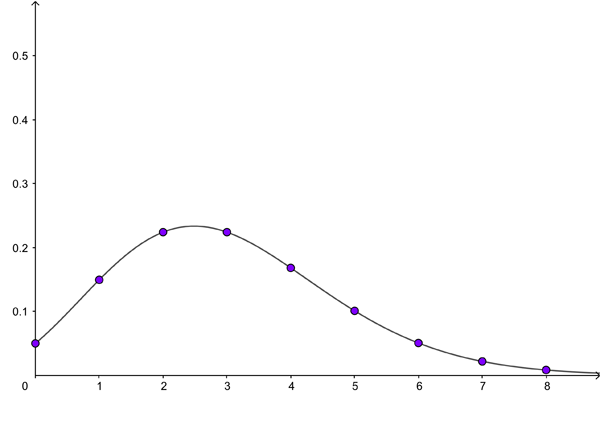
The Poisson distribution for a=3.
The mean of this distribution, also known as the expectation, is $a.$ In our example $a=3$. Loosely speaking, this means that if we switched our feed on lots and lots of times and each time counted the number of posts we see in the first minute, the average of those counts would be 3 — which is of course what we expect.
The variance of the Poisson distribution, which measures how the individual probabilities are spread out is also $a.$ Below are three more examples of the Poisson distribution, for $a=1$, $a=6$, and $a=10$.
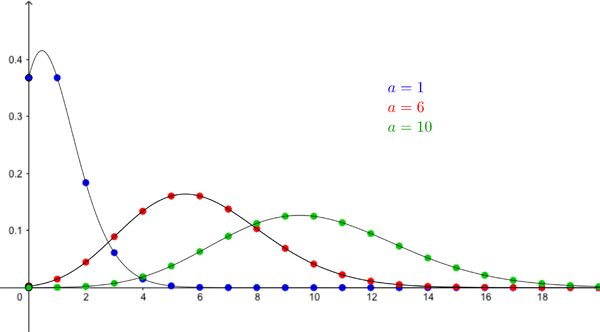
The Poisson distribution for a=1 (blue), a=6 (red), and a=10 (green).