
If you've ever marvelled at a rainbow, you have witnessed dispersion in action. Dispersion is where the speed at which a wave moves depends on its frequency (and so wavelength). (You can read a basic introduction to waves and their frequency and wavelengths in Why sine (and cosine) make waves and Give us a wave.)
The most familiar example is the refraction of the different colours that make up white light as they pass through a glass prism or are reflected inside water droplets to form a rainbow.
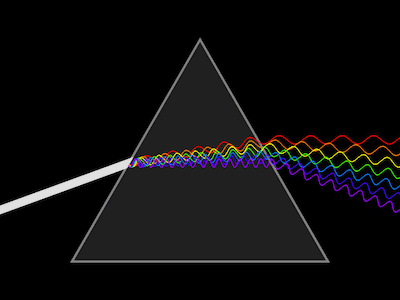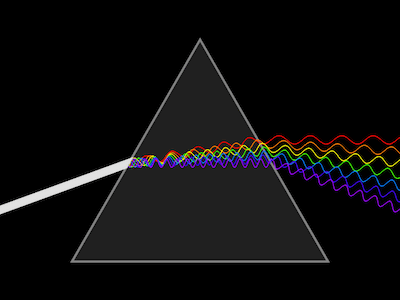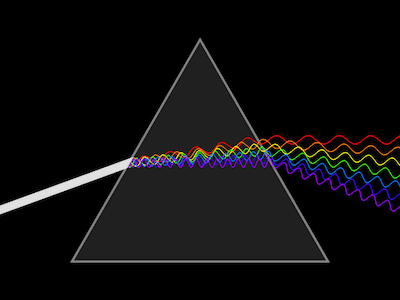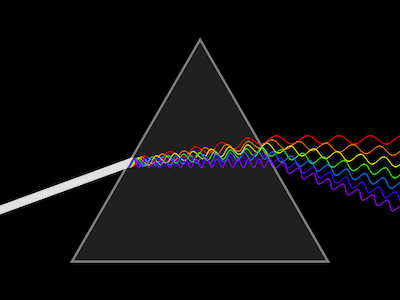
An illustration of the different wavelengths that make up white light being dispersed by a prism. (Image by Lucas Vieira - in public domain)
Refraction is a result of a ray of light being bent because it slows down as it passes from one medium to another. For a very crude analogy, think of pushing a shopping trolley from the road onto grass at an angle: it will change direction because the side of the trolley that hits the grass first will be slowed down first.
When light from the Sun travels through a vacuum (and to a very good approximation through air) all frequencies travel at the same speed c, roughly 300,000 kilometres per second. As the ray of light passes into water (or the glass prism), the frequency, and therefore colour, remains the same. However, its speed will change by an amount that depends on the frequency. This is because the atomic structure of water interacts differently with waves of different frequencies.
A measure of the slowing-down of light with frequency $f$ is given by the refractive index, $n(f)$ $$ n(f) = \frac{c}{v(f)} $$ where $v(f)$ is the speed of light of frequency $f$ in the medium the light is entering. For water, the refractive index barely changes as the frequency varies: $n(f)$ is around 1.34 for the violet end of the spectrum and around 1.33 for the red end. But this small amount of dispersion is enough to split sunlight into the beautiful spectrum of colours we see in a rainbow. (You can read more in our article Maths behind the rainbow.)
From ripples...
The behaviour of waves we see on the surface of water, whether ripples on a pond or waves in the sea, is affected by gravity and the surface tension of the water. For small ripples the wavelength is so short that only surface tension is important. In this case the speed (technically called the phase velocity) of the wave is $$ v=\sqrt{\frac{\sigma k}{\rho}} $$ where $\sigma$ is the surface tension of the water, $\rho$ is its density, and $k$ is the wavenumber, $k=\frac{2/pi}{\lambda}$. (You can read an introduction to the wavenumber in Maths in a minute: Give us a wave.) The shorter the wavelength (and the larger the wavenumber), the faster the speed of the ripple.
Gravity dominates the behaviour of waves with longer wavelengths. If such a wave is moving through deep water (in comparison to the wavelength) then the speed of the wave is $$ v=\sqrt{\frac{g}{k}} $$ where $g=9.81 ms^{-2}$ is the acceleration due to gravity. Here the longer the wavelength (and the smaller the wavenumber), the faster the speed of the wave.
There is dispersion in both of these cases – the speed of the waves depend on the wavelength. However, if a wave were moving through water that is shallow in comparison to its wavelength, then the speed of the wave would be $$ v=\sqrt{gh} $$ where $h$ is the depth of the water. Here there is no dispersion because the speed of the wave does not depend on the wavelength — it only depends on gravity and the depth of the water.
...to relationships
One way of understanding dispersion is to look at the dispersion relations for these different cases. A dispersion relation describes how the wave's angular frequency, $\omega = 2\pi f$, depends on the wavenumber $k$. (For an introduction to angular frequency see Maths in a minute: Give us a wave.)
For waves in shallower water, the dispersion relation is $$ \omega (k) = k\sqrt{gh}. $$ This means that the the angular frequency $\omega(k)$ is directly proportional to the wavenumber $k$ – it is a linear function of $k$.
But for ripples, and for waves of longer wavelength in deep water, the respective dispersion relations, respectively, are $$ \omega(k) = \sqrt{\frac{\sigma k^3}{\rho}} $$ and $$ \omega(k) = \sqrt{gk}. $$ Both of these dispersion relations are non-linear functions of $k$. The non-linearity, or linearity, of the dispersion relation, governs whether there is, or isn't dispersion.
About this article
This article was produced as part of our coverage of the Dispersive hydrodynamics: mathematics, simulation and experiments, with applications in nonlinear waves programme hosted by the Isaac Newton Institute for Mathematical Sciences (INI). You can find more content about the programme here.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
