Think of a wave – what comes to mind? The ocean swell rocking a boat? Ripples on a pond? The loop moving down a whip as it is cracked? Or perhaps your favourite song pumping out of your stereo speaker? Waves happen when a disturbance (of, say, the flat surface of the water by the ripple, the stillness of the air by a sound wave) moves over time.

Sine time

Mathematically the simplest and most perfect wave is described by a sine (or cosine) function. You can read a simple introduction to them in Why sine (and cosine) make waves. For example, the function $$ y(x,t) = A \sin \left(\frac{2\pi}{\lambda} x-vt\right) $$ describes a sine wave travelling in the $x$ direction with speed $v$ over time $t$. Here $A$ is the amplitude – the maximum displacement of the wave from equilibrium. And $\lambda$ is the wavelength – the distance between two peaks of the wave.

A snapshot in time and space

You might be more familiar with thinking of a sine or cosine function of one variable. You can think of the function $$ y(x) = A \sin\left(\frac{2\pi}{\lambda} x\right) $$ as being like a snapshot in time of the moving wave. This function is shown in red in the plot below, where $y(x)$ is plotted against $x$.

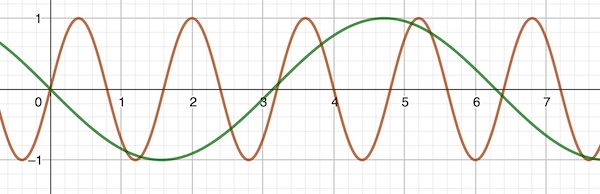
And similarly the function $$ y(t)=A \sin (-vt) $$ is a snapshot of the moving wave in space – it describes the behaviour of the wave over time at the fixed point in space you are standing in. You can see this function in green on the plot above. This time the function $f(t)$ is plotted against time $t$.

Many ways of saying the same thing

The quantities of amplitude ($A$), wavelength ($\lambda$) and speed ($v$) are all we need to completely describe our wave. But there are many equivalent ways of describing our wave with other quantities.

For example, because speed is just distance travelled per unit time, all waves must obey the equation $$ v = \lambda f $$ where $f$ is the wave's frequency – how many times the wave completes a full cycle in one second. From the frequency you can determine the period, the time it takes for a whole cycle of the wave to pass a certain point: $$ T=\frac{1}{f}. $$ Then we could rewrite our wave in terms of frequency $f$ or period $T$: $$ y(x,t) = A \sin\left(\frac{2\pi}{\lambda} x- \lambda f t\right) = A \sin\left(\frac{2\pi}{\lambda} x- \frac{\lambda}{T} t\right). $$

However we can rewrite our wave function in much simpler ways with other wave parameters.

In phase

You can describe a complete cycle of a wave in terms of the distance it travels in once cycle (the wavelength, $\lambda$) or the time it takes (the period $T$). But equivalently you can think of one complete cycle of a wave in terms of angles (you can see why here). One whole cycle of the wave equates to moving through an angle of 360 degrees, or $2\pi$ radians. The phase of the wave indicates how far through a cycle the wave is: the phase is 0 radians at the beginning of a cycle, increases over one cycle, passing $\pi$ at the midpoint. At the end of the cycle the phase can simultaneously be thought of as $2\pi$, as it's the end of one cycle, and 0, as it's also the beginning of the next cycle.

Thinking in terms of the phase of the wave can make writing the wave function simpler. The angular frequency of the wave is $$ \omega = 2 \pi f = \frac{2\pi}{T}. $$ which you can think of as the rate of change over time of the phase of the wave.

Similarly the angular wavenumber (often just called the wavenumber) of the wave is $$ k = \frac{2\pi }{\lambda} $$ which describes how much of the wave's cycle is completed in one unit of distance, or the rate of change over space of the phase of the wave.

Now you can write our wave function in this much simpler form: $$ y(x,t) = A \sin(kx-vt). $$ As we've seen you can write the wave function in different ways, depending on what property we are interested in. They are all give different, yet related ways of describing a wave. And if all of these wave properties are constant, you get the following relationships between them: $$ k = \frac{2\pi }{\lambda} = \frac{2\pi f}{v} = \frac{\omega}{v}. $$

Wave equation

The wave function $y(x,t)=A \sin(kx-vt)$ we gave above is a solution to the wave equation: $$ \frac{d^2 y}{dt^2} = v^2 \frac{d^2 y}{dx^2} $$ This is a partial differential equation (you can read about them here) where the left side gives information of how quickly the height of the wave changes over time and the right gives information of how quickly the height of the wave changes over distance (these are called double derivatives – see here for an easy explanation.)

Waves arising in nature can be complex

Wave equations like this one arise in lots of physical situations, from the sound made by musical instruments to the seismology of stars. Other more complex wave equations arise in the study of fluid mechanics, such as the Euler equations for the movement of water under an ocean wave and the Navier Stokes equations, and even in quantum physics. In these more complex wave equations the wave function that explicitly defines the position of a point on the wave at any time is harder, or even impossible to find. In these cases methods for approximating the solution are used to find a function that closely matches the desired behaviour of the wave, using techniques from computational fluid dynamics.

About this article

This article was produced as part of our coverage of the Dispersive hydrodynamics: mathematics, simulation and experiments, with applications in nonlinear waves programme hosted by the Isaac Newton Institute for Mathematical Sciences. You can find more content about the programme here.

Rachel Thomas is Editor of Plus.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.