
Starting from their origin as an abstraction of the concept of symmetry, groups have become a core part of the language of modern mathematics and theoretical physics. On this page, find out how groups can help describe roots of polynomials, holes on a surface, and even the laws of physics!
What is a group?
In mathematics and physics, an important notion is that of a symmetry: a transformation from an object to itself which leaves all its features unchanged. Across the 19th and early 20th centuries, mathematicians gradually realised that all collections of symmetries had in common a list of key properties:
- The ability to compose symmetries to get a new symmetry (closure/associativity)
- The ability to undo symmetries (inverses)
- The existence of a do-nothing symmetry which leaves the object untouched (identity).
A group abstracts a collection of symmetries, taking these key properties as its starting point. That is, a group is a set of elements with a combining operation that satisfies exactly the three properties listed above.
Find examples of groups and more ways to think about what a group is below:

Groups: Basics — This package introduces what a group is and some basic concepts in group theory.
Nowadays, groups are ubiquitous throughout mathematics and theoretical physics. To describe polynomials, we talk about their Galois group. To describe the topology of shapes, we talk about their fundamental group. And modern theories of physics take the symmetries of the universe as their starting point. Find out more details about how groups are used throughout maths and physics below.
How are groups used in...
Finding the laws of physics
The world around us possesses many symmetries. There is time-translation symmetry: the belief that the laws of physics will be the same tomorrow as they are today; space-translation symmetry: the laws of physics are the same on Mars as they are here on Earth; and so on.
In the early 20th century, Emmy Noether proved the amazing result that any symmetry of our Universe gives rise to its own law of physics. Collectively, the laws derived from Noether’s theorem are called conservation laws, since each law says that a certain physical quantity is conserved over time. Time-translation symmetry corresponds to conservation of energy, while space-translation symmetry corresponds to the conservation of momentum. Hence understanding the symmetries of our Universe, a job for group theory, allows us to understand the laws of physics.
Read more about Emmy Noether and her work here:
Emmy Noether and the power of symmetry — Find out about how Emmy Noether forever tied physics together with symmetries.
In fact, most modern formulations of physics take symmetry as their central guiding principle. Rather than formulating a theory first and then looking for its symmetries later, physicists first decide what symmetries their theory should possess and then see how reality fits in with that. The approach has had startling success. Several fundamental particles, including the famous Higgs boson, were predicted to exist based on the assumption that certain (rather abstract) symmetries exist, and only later discovered in experiments. The hope is that symmetry will eventually guide us to the hotly sought after theory of everything. Find out more in the article below:
Symmetry making and symmetry breaking — A closer look at the power of symmetry in modern physics.
Solving polynomial equations
A polynomial equation is an equation composed of a variable $x$ and its powers. For example, $x^3 + x + 1 = 0$ is a polynomial equation (see here for more about polynomials).
You may have learned a formula to solve quadratic equations in school: equations of degree 2 where $x^2$ is the highest power of $x$. In the 16th century, more complicated formulas were discovered which solved cubic (degree 3) and quartic (degree 4) equations. But what about higher degrees? For almost three centuries mathematicians were stuck, until in the early 1800s the mathematician Évariste Galois came and recast the problem into the language of group theory.
Galois Theory investigates the roots (the solutions) of polynomials by constructing a group, called the Galois group, from each polynomial. Understanding the Galois group of a polynomial then helps us in understanding its roots.
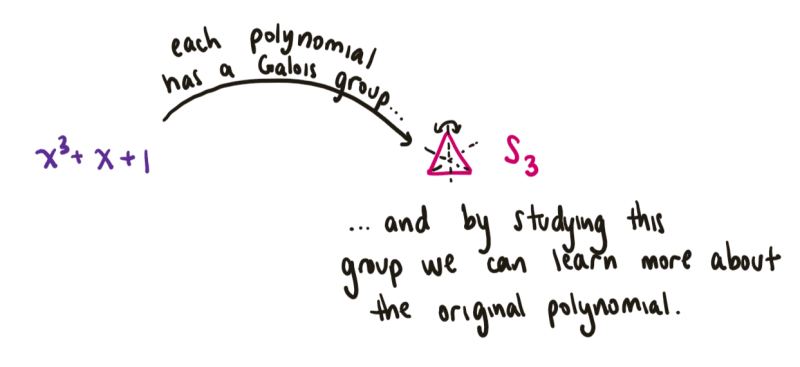
Importantly for our story, the way the Galois group decomposes into smaller groups (and in particular whether the group satisfies a property called solvability) determines whether or not the roots of that polynomial can be written in terms of $+, -, x, /,$ and $n$th roots. Because the group of all ways to rearrange 5 generic elements is not solvable, there are degree 5 (quintic) polynomials whose roots cannot be expressed just in terms of these symbols. That is, mathematicians were stuck because there is no formula for solving a quintic equation!
Read more about Évariste Galois and Galois theory below:
Stubborn equations and the study of symmetry — An impossible equation, two tragic heroes and the mathematical study of symmetry.
Describing holes
Topology is the study of shapes, where we count two shapes to be the same if one can be stretched and squeezed into the other. For example, a topologist would say that a doughnut and a coffee mug have the same shape, because both are solid and have exactly one hole where you can put your fingers through to hold.
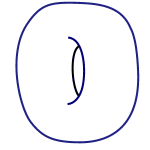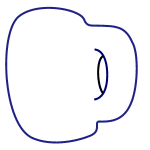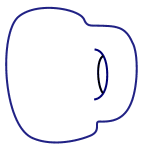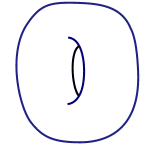
An inflatable swimming ring, on the other hand, has one hole in the middle to hold; but is also hollow: it has another "hole" on its inside! It seems like the "hole" where the air goes is a different kind of hole than the "hole" where our hands can go, but what exactly do we mean by that? We need some language to describe holes more precisely.
In the early 20th century, mathematicians invented two ways to describe holes: homotopy and homology. Both of them assign a sequence of groups to a shape, and the groups describe what kinds of holes the shape has. Different groups correspond to different kinds of holes. Using the language of groups, we can make precise the idea that in an inflatable swimming ring, the hole where the air goes is two-dimensional, whereas the hole where our hands can go is one-dimensional.
Read more about the fundamental group (the first of the homotopy groups) here:
Maths in a minute: The fundamental group — Topology considers two objects to be the same as long as you can morph one into the other without breaking it. But how do you work with such a slippery concept? One useful tool is what's called the fundamental group of a shape.
And about what it means for a hole to be one- vs two- dimensional here:
Spheres within spheres: a journey through many dimensions — Learn what it means for a hole to be one- vs two- dimensional in the context of an exciting recent breakthrough in the world of topology.