It's good to have a sense of balance, even in physics. In the 1920s the physicist Paul Dirac developed an equation to describe the behaviour of electrons. The equation contained mathematical terms that had no physical interpretation, so to balance things out, Dirac swiftly invented one. He stipulated that each electron should come with a anti-electron, called a positron, which is what those extra components of the equations represent. A few years later, positrons were duly discovered in cosmic rays, and today they benefit the millions of people who get their medical diagnoses from positron emission tomography (PET) scans.

You've got symmetry to thank for your PET scan.

That seems like an amazing fluke, but it's not the only example of theory preceding discovery. A preference for balance — for symmetry to be precise — is what guides much of modern physics. We tend to think of symmetry as something visual, but it's actually a wider concept. Symmetry is immunity to change. A square is symmetrical because it looks the same after it's been rotated around its centre by 90 degrees, or reflected in one of its axes. In physics, finding something — a quantity or pattern — that doesn't change can indicate you're on to something fundamental.

An example are the laws of conservation: the fact that certain quantities, such as energy, momentum, or electric charge, can't suddenly vanish or be created from nothing. They are conserved quantities. In 1915 the mathematician Emmy Noether linked those conserved quantities to symmetries. Conservation of angular momentum, for example, implies that the laws of mechanics are invariant under rotation: a physicists conducting an experiment will see the same results whether the experimental set-up is facing North, South, East or West, or, indeed, anywhere in-between. Noether's theorem says that conservation laws are equivalent to symmetries in the laws of nature: every conservation law comes with a symmetry, and vice versa. (See here to find out more.)

That's a nice deep link between symmetry and physics, but we can go even further. Symmetries can help us deduce things about the Universe without even looking at it. For example, it can help us deduce that a force like gravity must exist.

Gravity and motion

The reason we can indulge in fine dining on a train is that objects behave the same way when they are travelling at constant velocity as they do when they are at rest.

The fact that the laws of nature remain invariant under rotations means that a person locked in a windowless box has no way of telling which direction they are looking in. Something similar would remain true if the box were set into motion. As long as the box is moving at a constant velocity, no experiment or test would be able to tell the inhabitant at what speed they are moving, or even if they are moving at all. It's something we've all experienced when travelling by train: as long as the train isn't speeding up, slowing down, or swerving, and the tracks aren't too bumpy, things inside the train behave exactly as they do outside on the platform. It's another symmetry: the behaviour of things remains invariant when you swap a frame of reference (the inside of the box or train) going at one constant velocity for another frame of reference going at another constant velocity.

Now what if the box were accelerating, that is, speeding up or slowing down? Will its inhabitant be excluded from the symmetries of nature? The answer is no, and that's where the force of gravity comes in. The box inhabitant will notice that something is happening, because everything inside the box that is not nailed down will suddenly move towards one of its walls. But it turns out that gravity can do just the same thing. If the box were to move into the vicinity of a heavy body of just the right mass, the body's gravitational pull could make the things in the box move in the same way as the acceleration appears to do. The inhabitant has no way of telling whether it's gravity or acceleration doing the moving. Thus the symmetry extends a little further, allowing us to swap observers in accelerating boxes with observers in non-accelerating boxes that feel gravity, without anyone noticing.

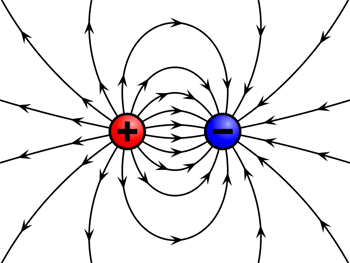
A positively and a negatively charged particle generate an electric field. A static electric field is described by the electric potential (voltage) at each point, but the field won't change if you change the voltage everywhere by the same amount. This invariance under changes in voltage is a gauge symmetry of electromagnetism. Image: Geek3, CC BY-SA 3.0.

Notice that gravity is crucial in all this. In a world without gravity, the box inhabitant would definitely be able to tell acceleration from non-acceleration. The symmetry can only hold in worlds where a force very much like gravity, which can mimic the effects of acceleration, exists. The symmetry requires the force to exist, and you could deduce it exists even had you never felt it.

Symmetry and the other forces

Albert Einstein, who famously noted that motion is relative, built his theory of gravity, called general relativity, around such a symmetry principle. A little after the theory's publication in 1915, physicists realised that something similar works for other forces too: if you stipulate that certain symmetries hold, then the forces must exist. "The [resulting] theories, known as gauge theories, are very unusual," explains John Barrow, mathematician and cosmologist at the University of Cambridge (you can see excerpts of our interview with him below). "In some sense they require the forces to exist in order to be self-consistent."

The other forces of nature, electromagnetism, and the strong and the weak nuclear forces, govern the behaviour of elementary particles, so symmetries can tell us something about those particles too. "Each of these theories has a particular, rather abstract pattern that is preserved," explains Barrow. "The preservation of that pattern is responsible, not just for the rules governing how the forces behave, but also for dictating which particles can exist. This is a very powerful situation. Physicists have become very impressed by the power of symmetry, and symmetry arguments, to derive the theory which is going to govern elementary particles."

And this isn't all. In the 1960s physicists suggested that two of the fundamental forces, electromagnetism and the weak force, were in fact two sides of the same coin: a unified electroweak force. They came up with a unified mathematical framework, a gauge theory, which describes them both. "The underlying description of these forces is very much like Maxwell's [older description of electromagnetism], so that's unification," explains John Ellis, Clerk Maxwell Professor at King's College, London. "It's a more complicated set of equations, but, in principle, they're relatively simple, because there's a symmetry that relates them together." (You can find out more about these symmetries by means of an analogy to economics in our Financial ether package.)

The hope is that the symmetry can be extended further, to include the other forces too. "It's as though you've got four patterns [corresponding to the four forces we see], like pieces of a jigsaw puzzle, and you want to join them together so that they become part of a much larger pattern," says Barrow. "You hope that the joining together of the pieces places some new constraints on what is in the individual pieces, which might be predicting new particles or new things that you can check."

Symmetry breaking

This pencil is bound to topple. The laws of nature don't determine which way it'll topple — they are rotationally symmetric. Once it has toppled one way, the situation is no longer symmetric. But this asymmetry is an asymmetry of an outcome of the laws of nature, rather than the laws themselves.

But if that is the case, if the forces are, in some sense, one and the same, how come we perceive them as different forces today? The answer is that an underlying symmetry can go into hiding without actually disappearing from the theories. As an example, think of a pencil balancing on its tip, which is in danger of toppling due to the force of gravity. "The law of gravity is perfectly democratic with regards to directions," explains Barrow. "It doesn't say that [the pencil] always has to fall over in the direction towards the pole star. But in a perfect vacuum at zero temperature, quantum fluctuations will always make it fall in some direction. When it falls the symmetry with respect to direction is broken." Thus, an outcome of the laws of nature does not have to possess the same symmetry as the laws themselves.

"We [ourselves] are examples of [broken symmetry]," says Barrow. "You and I are located at particular positions in the Universe at the moment, but the laws of electromagnetism and gravity which are responsible for us, at some basic level, don't have preferred positions in the Universe. This is one of the secrets of the Universe, if you like. How it can have all these complicated things in it. If the outcomes of the laws had to possess the same symmetries as the laws then there wouldn't be anything in the Universe. It would be a rather boring place."

As far as the forces are concerned, the idea is that, as the Universe cooled down from the Big Bang, a time at which it was uniform and highly symmetrical, the forces sort of crystallised out and became different. "The expectation is at first everything was highly symmetrical and then gradually certain thresholds were reached," explains Barrow. "You reach a particular temperature and the strong force will become different to the others, so a symmetry will have broken, and eventually the weak force, and electromagnetism, will become different forces. So as the Universe cools there are these symmetry breaking moments, rather like the pencil falling in one direction."

Symmetry and reality

All this may seem like a very tall order. It's hard to believe that our Universe, so full of hugely complex phenomena, should obey some rather simple laws that are based on the assumption of symmetry. Yet this kind of theorising has led to quite a few discoveries. The unification of the weak and electromagnetic force, and the breaking of the underlying symmetry, required the existence of comparatively heavy particles called Z and W bosons. The fact that particles could be heavy at all, and not, as symmetry would decree, massless, in turn required the existence of the famous Higgs boson. Each of these particles did turn out to exist: the Z and W bosons were discovered at CERN the 1980s, and the Higgs boson in 2012.

It's also worth noting that simple theories don't necessarily mean simple calculations. The theory physicists believe governs the strong nuclear force, for example, has a relatively simple overall structure, but the calculations you need to perform to actually describe real-world phenomena are so complicated, they defy even the fastest supercomputer. "We have mathematical arguments that lead us to a candidate [theory], but we don't know how to solve the laws to work out the outcomes," says Barrow. "The outcomes are much more complicated. And they don't have to possess the same symmetries as the laws."

So is this it then? Are physicists going to forget about experiments and rely solely on theory? Not quite. "[Particularly in particle physics] I think there's been a dog race [over the last century or so], between the experimentalists finding particles that the theorists had not predicted and the theorists predicting particles that, later, the experimentalists discovered," says Ellis. "Both happen, and I think this reflects the fact that science advances through this continual dialogue between theory and experiment."

Further reading

To find out more about how the laws of nature relate to their outcomes see Stuff happens: Laws versus outcomes.

This article is part of our Stuff happens: the physics of events project, run in collaboration with FQXi. Click here to see more articles and videos about the laws of nature and their outcomes.

About this article

Marianne Freiberger is Editor of Plus. She interviewed John D. Barrow and John Ellis in December 2015.