
Maths in a minute: Polynomials
Polynomials are best understood by creeping up on them. Take a look at the expression $$2x+1.$$
It consists of a variable $x$ which is multiplied by $2$. The constant $1$ is then added on. This an example of a linear expression. If you treat it as a mathematical function $f(x)=2x+1$ and plot its graph, you get a straight line (see the figure below). The general form of such a linear expression is $$a_1x+a_0,$$
where $a_1$ and $a_0$ are two constants.
A quadratic expression is of the form $$a_2x^2+a_1x+a_0,$$
where $a_2$, $a_1$, and $a_0$ are constants. The difference to a linear expression is that we've added on a multiple of the square of $x$. An example of a quadratic expression is $$x^2.$$
Here we have $a_2=1$ and $a_1=a_0=0.$ If you treat this expression as a mathematical function and plot its graph, you get a parabola (see the figure below). We don't need to stop here. We could also add on a multiple of the cube of $x$ to get the general cubic expression $$a_3x^3+a_2x^2+a_1x+a_0,$$
and then add on a multiple of $x$ to the fourth power to get the general quartic expression $$a_4x^4+a_3x^3+a_2x^2+a_1x+a_0.$$
Taking this further, a polynomial in the variable $x$ is any expression formed by taking multiples of the powers of $x$ and adding them together (note that $a_0=a_0x^0$, so even the last term can be viewed as containing a power of $x$). We can write a general polynomial as $$a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0,$$
where $n$ is the highest power of $x$ that appears in the expression and $a_n$, $a_{n-1}$, etc, up to $a_0$ are constants. These constants are called the coefficients of $x$ in the polynomial. The word "polynomial" captures the fact that a polynomial is made up of many terms. It's a mixture of Greek and Latin, derived from the Greek word "poly", which means "many", and the Latin word "nomen", which means "name", but in this case can be interpreted as meaning "term".
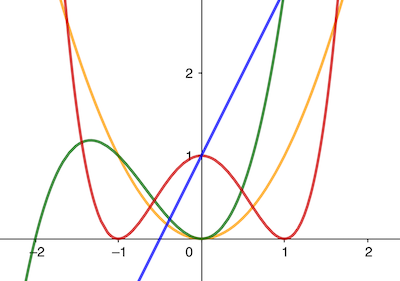
The blue line is defined by the polynomial function f(x)=2x+1, the orange parabola by f(x)=x2, the green curve by f(x)=x3+3x2, and the red curve by f(x)=x4+4x3+6x2+4x+1.
Specify and generalise
There are a couple more things we need to say to make our definition of a polynomial complete. Note that in the above we haven't specified what kind of number the variable $x$ represents, and what kind of values the coefficients can take. When you meet polynomials at school, you usually assume that the coefficients, as well as the variable, are all real numbers. There might be situations, however, where you want the variable and/or coefficients to only take integer or fractional values, or where you may allow them to take on complex values. Generally, when talking about polynomials, you should specify the sets of numbers the coefficients and the variable belong to. For example, you might talk about a polynomial in a real variable $x$ with integer coefficients.
The second thing to note is that you can also have polynomial expressions in more than one variable. The expression $$x^2+xy+y^2$$
is an example of a polynomial with two variables and the expression $$x^5y^4z^3+2x^2z+5y^3z^7$$
is an example of a polynomial with three variables. In general, a polynomial in several variables is a sum of many terms, each of which is the product of powers of these variables multiplied by a coefficient.
Geometry from algebra
Finally, we should point out the link between polynomials and geometry. As we've seen above, polynomials in one variable can define lines and curves. The link comes about through the notion of a coordinate system. Similarly, a polynomial in two variables can define a surface. For example, the surface shown below is defined by the polynomial function $f(x,y) = x^3+y^3+1$. Polynomials with more than two variables can also be thought of as defining geometric objects, though in this case the objects live in higher dimensions we can no longer visualise. See Maths in a minute: Algebraic varieties to find out more.
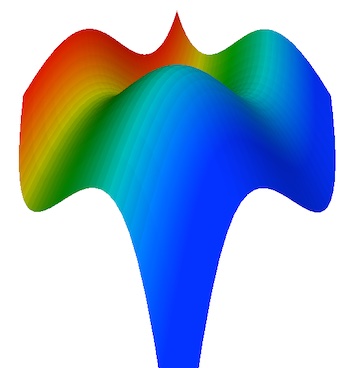
This surface is defined in a three-dimensional coordinate system by the equation f(x,y)=x3+y3+1.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
