The doubling time of a disease

The doubling time of a disease is the time it takes for the number of cases of the disease to double. For example if in an outbreak of a disease in a particular town there are 40 cases on Monday and 80 cases on Thursday, then the doubling time is three days.

Back to the Epidemiology for beginners collection.

The doubling time is a powerful concept because it allows you to quickly work out how fast the disease is likely to spread: 40 cases on Monday, 80 on Thursday, 160 on Sunday, etc. It is intimately related to the growth rate of the disease which, loosely speaking, tells you by how much the number of cases increases or decreases each day and which we explore in this article.

Doubling time and growth rate are both quantities that can be estimated from the data when a disease has broken out. You can also calculate the doubling time from the growth rate, but the relationship is a little more subtle than you might think at first.

For example, for a growth rate of 0.33, which translates to 33%, you might think that you have to wait three days for the number of cases to increase by 100%, that is, you might expect a doubling time of three days. But this is not correct. In reality the doubling time is a lot shorter; just over two days. The reason for this is essentially the same as the reason why, if you're not careful, compound interest gets you into debt quicker than you might have thought when you took out the loan.

A little about growth rate

The growth rate of a disease captures how quickly the number of infections are changing day by day. It is modelled using an exponential curve:

$N(t) = c e^{\lambda t}$

Here $N$ is the number of cases, which depends on time $t$ measured in days, and $\lambda$ (pronounced "lambda") is the growth rate of the disease per day. The number $c$ is the number of cases at time $t=0$ , that is, the moment of time you are trying to project forward from.

The number $e$ is a mathematical constant approximately equal to 2.719. The reason it appears here is that it is intimately connected to growth that is continually compounded. See here for an explanation of the maths behind this, and here for a general explainer of the concept of growth rate.

When you first hear the term "growth rate" you might think that $\lambda$ gives you the increase in cases per day, particularly as it can also be expressed as a percentage. But that’s not quite correct. The day-on-day increase, according to our formula above is

$N(t+1)-N(t) = c e^{\lambda (t+1)}-c e^{\lambda t},$

which simplifies to

$c e^{\lambda t}\left(e^\lambda -1\right).$

As a percentage of $N(t)$ this is

$\frac{c e^{\lambda t}\left(e^\lambda -1\right)}{c e^{\lambda t}}\times 100 = 100(e^\lambda -1).$

Coming back to our example of $\lambda =0.33$ , we see that the percentage growth per day is not 33%, as you might have thought, but

$100(e^{0.33}-1)=39\% ,$

which is quite a bit higher. Only when $\lambda$ is small (say around $\lambda <0.1$ ) can we take the value of $\lambda$ itself as an estimate of the day-on-day increase (this is because for these small values $\lambda$ is a good approximation of $e^\lambda -1$ ).

Calculating doubling time from growth rate

Now let’s calculate the doubling time from our model of growth rate. We would like to find the length $d$ of the time period it takes for cases to double. Mathematically, we need to solve for $d$ the expression

$N(t+d)=2N(t).$

Using the formula above this means we need to solve for $d$ the expression

$c e^{\lambda (t+d)}=2 c e^{\lambda t}.$

Taking logarithms of both sides of the equation gives

$\ln {c}+\lambda (t+d) = \ln {2}+\ln {c}+\lambda t.$

Solving for $d$ gives

$d=\frac{\ln {2}}{\lambda }.$

This tells us how the doubling time $d$ depends on the growth rate $\lambda$ . Here is the plot of the relationship. It shows that doubling time does not increase linearly with growth rate, but instead plummets quite dramatically as $\lambda$ increases.

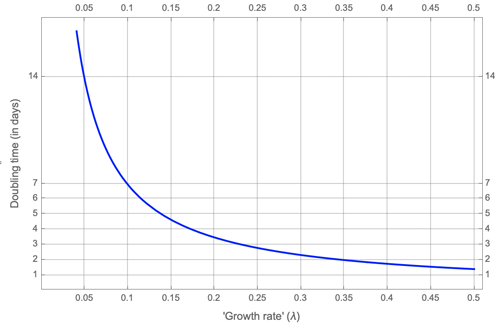
Doubling time in terms of growth rate, as given by the formula we calculated.

Coming back to our example above, for a growth rate of $\lambda =0.33$ , our formula tells us that the corresponding doubling time is

$d=\frac{\ln {2}}{0.33} = 2.1,$

which is just over two days as we claimed.

About this article

Marianne Freiberger is Editor of Plus. This article was produced with Julia Gog, Professor of Mathematical Biology at the University of Cambridge and co-lead of the JUNIPER network. Gog is also a member of the Scientific Pandemic Infections group on Modelling (SPI-M), an advisory group of the Department of Health and Social Care which provides expert advice to the UK government based on infectious disease modelling and epidemiology and fed results into the Scientific Advisory Group for Emergencies (SAGE) during the COVID-19 pandemic.

This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.