Chickens may behave erratically when they are headless, but with their heads screwed on, so new research shows, they are capable of an amazing form of disordered order.

Like the eyes of all animals, chickens' eyes contain light-senstive cells known as cones. There are five types of cones of different sizes packed into the retina of a chicken's eye. In many species the cones are arranged in a regular pattern, for example the familiar hexagonal pattern found in insects' eyes. In chickens, however, there doesn't appear to be any pattern at all: the arrangement looks completely random.

This diagram shows the distribution of the five types of light-sensitive cells known as cones in the chicken retina. (Image courtesy of Joseph Corbo and Timothy Lau, Washington University in St. Louis.)

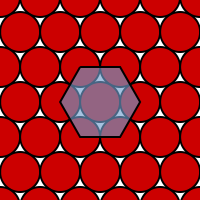
The optimal packing of circles in the plane. The centres of circles form a regular lattice.

But only until you take a closer look — it turns out that the crazy arrangement is the solution to a subtle packing problem. Imagine you want to fit as many dots as possible onto a piece of paper, but that each dot must stay a distance d away from any other dot. One way of doing this is to imagine each dot as sitting at the cente of a circle with radius d/2. Your task now is to fit as many circles as possible onto the paper, with none of them overlapping. And it turns out that the best way of doing this in the two-dimensional plane is to arrange your circles as shown on the right. The centres of the circles — your dots — are arranged in a regular lattice.

Now imagine that your dots come in two types: big black ones and little red ones. Each dot must stay a certain distance from all other dots no matter what colour, but that distance, which defines an exclusion zone into which no other dot can enter, is different for black dots and red dots. To complicated matters further, imagine that dots want to stay away from dots of the same colour more than they want to stay away from dots of another colour. This means that each dot comes with two exclusion zones: one into which no other dot can enter and a larger one into which dots of the same colour can't enter. The task of fitting as many dots as possible into your picture now becomes a lot harder.

The figure below illustrates this conundrum. On the left you see black and red circles which illustrate the personal exlusion zone of each dot: no other dot can enter here. That personal exclusion zone is bigger for black dots than for red ones. In the middle you see the larger exclusion zone of black dots, into which no other black dot should enter. And the picture on the right shows the larger exclusion zones of red dots, into which no other red dots should enter. The exclusion zones introduce two competing effects: dots of the same colour would like to arrange themselves on a regular lattice which, as we saw above, is best if you're dealing with just one colour. But alas, the other coloured dots' interference prevents them from achieving that perfect order.

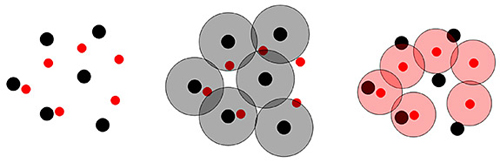
Exclusion zones around dots. (Image courtesy of Salvatore Torquato, Princeton University.)

The new research suggests that the seemingly crazy arrangement of cones in a chicken's retina is a result of similar packing rules, with cones of different types corresponding to the differently coloured dots in our example. But since the chicken eyes contain more than just two types of cones, the restraints are even more severe.

There is also another interesting feature about those cone arragnements. The scientists behind the new study found they exhibited a feature called disordered hyperuniformity, which people had known about theoretically but never observed in nature. It's an arrangement that is uniform over large distances, but disordered over small ones. "Because the cones are of different sizes it's not easy for the system to go into a crystal or ordered state," says Salvatore Torquato of Princeton University and one of the authors of the new study. "The system is frustrated from finding what might be the optimal solution, which would be the typical ordered arrangement. While the pattern must be disordered, it must also be as uniform as possible. Thus, disordered hyperuniformity is an excellent solution."

Packing as many cones as possible into the retina is important. We know from other animals that any arrangement that isn't optimal results in impaired vision. So it's likely that nature's solution to the packing problem in chickens' eyes is also the best possible. "These findings are significant because they suggest that the arrangement of photoreceptors in the bird, although not perfectly regular, are, in fact, as regular as they can be given the packing constraints," says Joseph Corbo, of Washington University in St. Louis, and another author of the study, which has been published in Physical Review E.

In mathematics packing problems have a long history. One of the most famous ones asks how to stack oranges so as to fit as many as possible into the available space. It turns out that the packing system you see in greengrocer's shops, with oranges in one layer nestling in the "holes" between oranges in the layer below is the best solution there is. Surprisingly, it took mathematicians nearly 400 years to prove that this conjecture, named after the famous scientist Johannes Kepler, is really true. The proof they finally did produce is highly controversial. You can find out more in Mathematical mysteries: Kepler's conjecture and Welcome to the maths lab.