
Inverse problems save the day

Inverse problems can solve crimes! Image: Klaus with K, CC BY-SA 3.0.
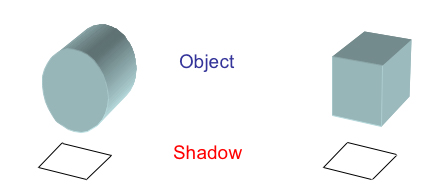
Inverse problems are mathematical detective problems. An example of an inverse problem is trying to find the shape of an object only knowing its shadows. Is it possible to do this at all? What sort of errors are we likely to make, and how much extra information is needed?
To solve an inverse problem, we need a mathematical model of the event — we need to understand what causes lead to what effects. Then, given the known effects, we can use maths to give the possible causes, such as deciding what shaped objects cast the shadows in this photo.
We also use maths in this situation to establish the limitations of the model and accuracy of the answer. In the example of shadows cast by objects, different causes (different shaped objects) may give very similar effects (cast similar shadows)!
Other examples of inverse problems are remote sensing of the land or sea from satellite images, using medical images for diagnosing tumours, and interpreting seismographs to prospect for oil. Another example is perhaps not the first thing that springs to mind when you think of maths: fighting crime.
Fighting crime with inverse problems
When a crime has been committed police must look at all the evidence left at the crime scene and work backwards to deduce what happened and who did it. Often, the evidence is a result of a physical process that is well understood — like a speeding car causing skid marks. So to find out the exact cause of the evidence — the speed of the car — the maths that describes the physics needs to be run backwards. This means solving an inverse problem.
Let's step into an ordinary day in the life of a police unit and see how mathematics can help fight crime. We are investigating a car accident and need to answer the question: was the car speeding?

The evidence available is the collision damage on the vehicles involved, witness reports, and tyre skid marks. Examining the skid marks can help reconstruct the accident. The marks are caused by the speed of the car as well as other factors such as braking force, friction with the road and impacts with other vehicles.
Mathematically we can use mechanics to model this event in terms of $s$, the length of the skid, $u$, the speed of the vehicle, $g$, the acceleration due to gravity and $\mu$, the coefficient of friction times braking efficiency. The model links the cause (the speed of the car) to the effect (the distance of the skid): $$ s=\frac{u^2}{2\mu g} $$ This can be rearranged so that given the skid distance we can mathematically determine the speed of the car, usually giving a lower bound: $$ u=\sqrt{2\mu gs} $$ As long as we have an accurate estimate of $\mu$, the value describing friction and braking efficiency, we can solve the problem and determine the speed of the car from its skid marks.
Saving lives with inverse problems
A Computerised Axial Tomography (CAT) scanner
Until relatively recently, if you had something wrong with your insides, you had to be operated on to find out what it was. Any such operation carried a significant risk, especially in the case of problems with the brain. However, this is no longer the case; doctors are able to use a whole variety of scanning techniques to look inside you in a completely safe way.
One example is a CAT scan that detects the effect passing through a body has on X-rays. In this scanner the patient lies on a bed and passes through the hole in the middle of the device. This hole contains an X-ray source which rotates around the patient. The X-rays from this source pass through the patient and are detected on the other side. The level of intensity of the X-ray can be measured accurately and the results processed.
As an X-ray passes through a patient, its intensity is reduced. The degree to which this happens depends upon what material the ray passes through: its intensity is reduced more when passing through bone than when passing through muscle, an internal organ, or a tumour.
Below we see an object irradiated by several X-rays with the intensity of the rays measured on a detector. Here some X-rays pass through all of the object and are strongly absorbed so that their intensity (recorded at the centre of the detector) is low, while others pass through less of the object and are less strongly absorbed. Effectively the object casts a shadow of the X-rays and from this we can work out its basic dimensions.
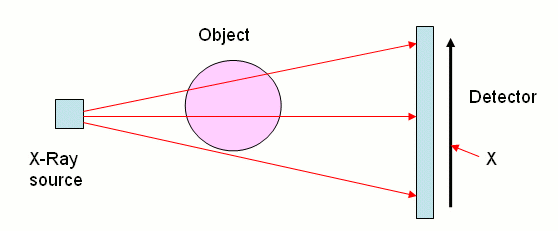
The intensity of the X-ray where it hits the detector depends on the width of object and the length of the path travelled both through the object and the air. By accurately measuring the intensity of many X-rays passing through an object from many different angles, the dimensions and size of the object can be reconstructed. Many mathematicians are working on improving the accuracy and efficiency of these techniques to make scanning easier on patients and more useful for doctors, and hopefully save more lives.
Maths saves the day
These are just two examples where mathematics helps us to work backwards from a result – whether it's from skid marks or detected X-rays in a CAT scan. There are many other ways that inverse problems can save the day!
This is an edited version of Chris Budd's article Crime fighting maths and his article with Cathryn Mitchell Saving lives: the mathematics of tomography. You can read the full articles here and here.