
Football sweepstakes: Levelling the playing field

Will you be doing a sweepstake for Euro 2020?
Not long to wait now! In just a few months' time people throughout Europe (and beyond) will don their football shirts and cheer on their favourite team to win the UEFA European Championships. Many workplaces will join in the fun by organising a sweepstake. People pay a nominal entry fee, are then randomly allocated one of the competing teams, and at the end of the competition the participant with the winning team wins all the money.
But you know what it's like. At the last FIFA World Cup I paid my £3 to enter the sweepstake and, with great anticipation, drew my allotted team. It was Panama, complete outsiders. My enthusiasm immediately disappeared, and I thought "Oh well, I'll have another go in four years' time". I am guessing that most of the other sweepstake participants went through similar feelings as soon as they realised that their team had no chance.
However, it doesn't have to be this way. I am proposing an alternative system, which should increase the fairness and excitement of the sweepstake.
Traditional team sweepstake
The sweepstake format traditionally used is that each participant is randomly assigned a team. However, the team which wins is invariably one of the favourites. Taking the World Cup as an example, we see that in the last ten tournaments the winner has been one of the top five teams (where the ranking is according to bookmakers' odds at the beginning of the tournament).
| Year | Winner | Ranking | Runner up | Ranking |
| 1982 | Italy | 5 | W Germany | 2 |
| 1986 | Argentina | 2 | W Germany | 6 |
| 1990 | W Germany | 4 | Argentina | 5 |
| 1994 | Brazil | 1 | Italy | 3 |
| 1998 | France | 2 | Brazil | 1 |
| 2002 | Brazil | 4 | Germany | 6 |
| 2006 | Italy | 5 | France | 6 |
| 2010 | Spain | 1 | Netherlands | 4 |
| 2014 | Germany | 3 | Argentina | 2 |
| 2018 | France | 4 | Croatia | 12 |
Thus the majority of the sweepstake participants, upon being allocated an unfancied team, will immediately lose interest. Furthermore, as the tournament progresses, and teams become eliminated, the overall engagement continues to drop.
Shirt number sweepstake
I am proposing a sweepstake based on shirt numbers. Basically, each participant is randomly allocated a shirt number for the tournament, and you get points every time that number scores. In the World Cup, the squads are numbered 1 to 23. For ease, I suggest just considering the last digit of the shirt number. For example, if you are allocated number 7, you get points every time a number 7 or 17 scores (thus there will be ten sweepstake participants). Consequently, in every game, you will almost certainly be invested in several players, and will be cheering for both teams! This should hopefully maintain interest and excitement for all the participants throughout the tournament.
Clearly, participants who are allocated numbers 1, 2 or 3 will get three possible squad numbers each whereas the other participants would only get two. However, as the goalkeepers' numbers tend to end in 1, 2 or 3, this possible edge is mostly mitigated.
Now, the question is, how many points should be awarded for each goal? If we look at the number of goals scored by the last digit of each shirt number for the last five World Cups we can see that numbers 9, 0, and 1 scored the most.
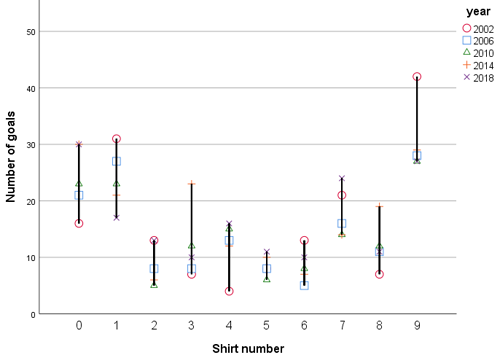
Last digit of shirt numbers for goalscorers in the World Cup from 2002 to 2018
This is not surprising as the forwards tend to wear shirt numbers 9, 10, and 11. Thus if we awarded 1 point for every goal, clearly this would not be fair for all the numbers. The sweepstake would be much more equitable if the lower scoring numbers received more points per goal.
The table below shows the mean (average) number of goals scored per tournament for each possible last digit of a shirt number. The last column of the table gives the highest mean (30.6 for the number 9) divided by the mean for the current row. We can see that number 9 scored 1.275 times as many goals as number 0, and 1.28571 times as many goals as number 1 and so on.
| Last digit of shirt number | Mean number of goals | Ratio compared to highest mean |
| 0 | 24 | 1.275 |
| 1 | 23.8 | 1.28571 |
| 2 | 9 | 3.4 |
| 3 | 12 | 2.55 |
| 4 | 12 | 2.55 |
| 5 | 8.6 | 3.55814 |
| 6 | 8.6 | 3.55814 |
| 7 | 17.8 | 1.7191 |
| 8 | 12 | 2.55 |
| 9 | 30.6 | 1 |
So if 1 point was awarded for every goal scored by number 9, 2.55 points awarded for every goal scored by number 8, 1.7191 points awarded for every goal scored by number 7 and so on, we would expect the total points for each number, i.e. for each sweepstake participant, to be the same value of 30.6 on average. This should hopefully lead to relatively fair sweepstakes where different shirt numbers would win at different tournaments.
However, carrying out awkward calculations such as adding 1.7191 when there is a goal scored may not be most people's idea of fun. The sweepstake would be much more user-friendly if these ratios were rounded. In the table below, the ratios have been rounded to the nearest 0.5, and doubled to make them integers, giving us the proposed points system for the sweepstake.
| Last digit of shirt number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Points per goal | 3 | 3 | 7 | 5 | 5 | 7 | 7 | 3 | 5 | 2 |
Illustrating this using the 2018 World Cup Final game between France and Croatia; player numbers 4, 6, 10 and 7 each scored 1 goal, and player number 17 scored 2 goals. In the sweepstake this would translate to 3 points for number 0, 5 points for number 4, 7 points for number 6, and 9 points for number 7.
So how fair does this points system turn out in practice? Applying it to the last five World Cup tournaments gives the following:
| Year | Winning number | Points | Runner up | Points |
| 2002 | 1 | 93 | 2 and 6 | 91 |
| 2006 | 1 | 81 | 4 | 65 |
| 2010 | 4 | 75 | 0 and 1 | 69 |
| 2014 | 3 | 115 | 8 | 90 |
| 2018 | 2 | 91 | 0 | 90 |
We can see that there are four different winners (numbers 1, 4, 3 and 2), and if we included a runner up prize this brings a further three sweepstake numbers into the picture (0, 6 and 8). This implies that the sweepstake system proposed is relatively fair in that many of the participants can expect a reasonable chance of obtaining a prize. Furthermore when comparing the points scores between the winner and runner up, it can be seen that they are generally very close, suggesting an exciting sweepstake.

Number 10s score highly: Lionel Messi celebrating a goal in a match against Ecuador. Photo: Agencia de Noticias ANDES, CC BY-SA 2.0.
One drawback to this points system is that it appears to slightly favour the lower goalscoring shirts. We saw earlier that number 9 scores 30.6 goals on average in a tournament, so would obtain 30.6 x 2 = 61.2 points on average. Number 4 would obtain 12 x 5 = 60 points on average. So both numbers expect roughly the same points score on average. However, because number 4 receives points less often but of a higher value for each goal, the points total it obtains each tournament will vary more. This means that it (and other low-scoring numbers) is more likely to obtain extreme values, which means it is more likely to win the sweepstake.
A possible way of adjusting for this is to include penalty shoot-outs. For example, all goals in a penalty shoot-out could be worth 2 points each for all shirt numbers. This would increase the relative points for the higher goalscoring shirts, as they are more likely to be taking penalties. Plus, it would have the added bonus of further extending the appeal of the sweepstake by incorporating the action beyond the in-game play.

About the author
Slim Khan is a Teaching Fellow at Warwick University, and is particularly interested in mathematics and statistics related to games and sports.
Comments
Nimit halai
Hey bud
This seems an interesting way of playing.
I have a list of 24 as im running a traditional sweepstake but thinking to split the the pot and run this too
What do you think is the best way to run this as there are 24 qplayers involved
Richard Geeves
Where did you get your statistics from please?