Geometrical music theory

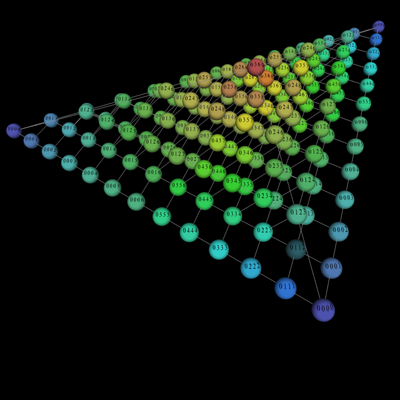
Four-note chords in geometrical music theory — the collections of notes form a tetrahedron, with the colours indicating the spacing between the individual notes in a sequence. In the blue spheres, the notes are clustered; in the warmer colours, they are farther apart. The red ball at the top of the pyramid is the diminished seventh chord. Near it are all the most familiar chords of Western music. Photo courtesy Dmitri Tymoczko.

With apologies to the musical Grease, mathematics and music go together like rama lama lama ke ding a de dinga a dong. You need to look no further than Plus to see how the links between the two have fascinated researchers for centuries — see all Plus articles tagged with the mathematics and music tag.

Clifton Callender from Florida State University, Ian Quinn from Yale University and Dmitri Tymoczko from Princeton University — all professors of music — have developed a new method of analysing music called "geometrical music theory" that is based on the mathematics entangled in the structure of music.

Their article Geometrical Music Theory, published in the April 18 edition of Science, outlines their theory that musical operations, such as transpositions, can be expressed as symmetries of n-dimensional space.

They categorise sequences such as chords, rhythms and scales into mathematical "families". The families can be represented by points on the complex plane, and different types of categorisation produce different geometrical spaces. The authors argue that through this method researchers will be able to analyse music more deeply and understand how music has changed over time. They also say that the theory will allow the comparison of many kinds of Western music, although only some non-Western styles. This is because the theory is based on concepts such as the "chord", which are present in nearly all Western styles, but not all non-Western styles.

The basis of geometrical music theory is that it provides a unified mathematical framework for musical events that are described differently depending on the scenario, but are fundamentally the same. For example, a "C" followed by the "E" and "G" above it may be described as a "C major chord," "an ascending C major arpeggio," "a major chord" and the list goes on. The authors describe five different methods of categorising such collections of notes. These are called "OPTIC symmetries," with each letter of OPTIC representing a different categorisation method that may, for example, look at what octaves the notes are in, their order of play, or how many times each note is played. Each categorisation focuses on one aspect of the music, ignoring the others. The five symmetries can then be combined together to produce different musical concepts, some familiar, some new. Three-note chords end up on a triangular doughnut while other chord types live on the surface of a cone.

Tymoczko believes that their theory can be used to investigate the differences between musical styles. "Our methods are not so great at distinguishing Aerosmith from The Rolling Stones," he said. "But they might allow you to visualise some of the differences between John Lennon and Paul McCartney. And they certainly help you understand more deeply how classical music relates to rock or is different from atonal music."

The authors even hope that through their work, new musical instruments may be developed. "You could create new kinds of musical instruments or new kinds of toys," said Tymoczko. He also envisaged new visual shows that could accompany the music. "Imagine going to a classical music concert where the music was being translated visually."

So next time you go see a visually spectacular Madonna or Kylie show, look at the big screens — you might learn some maths!

Further Reading

• The magical mathematics of music;
• Career interview: computer music researcher;
• Natural frequencies and music;
• Music and Euclid's algorithm;
• Or see all articles tagged with mathematics and music in Plus.