If we play with a compass and straightedge, we can discover all kinds of interesting shapes with arcs for sides. Let's look at some simple geometric shapes made of arcs.

An example is the Reuleaux triangle. It is formed from the vertices of an equilateral triangle, as shown below. Place the needle of your compass into each vertex and draw an arc of a circle connecting the other two vertices. Each of the three arcs defines a 60° angle at the vertex that corresponds to the centre. The Reuleaux triangle is the only arc-sided shape whose vertices (corners) are also the centres of the arcs that make up the sides.

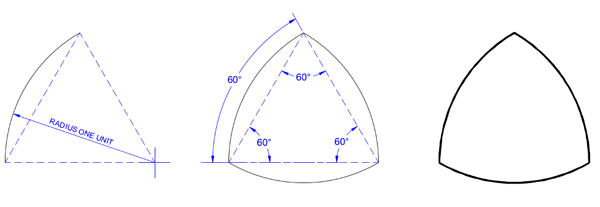
A Reuleaux triangle (right) is constructed from an equilateral triangle.

Generally, the shape of an arc of a circle is defined by two pieces of information: the radius of the circle and the angle the arc subtends at the centre of the circle, as shown above.

We can find other arc-sided shapes with interesting relationships between the centres of the arcs and the vertices of the shape. For each of the three shapes below, arcs drawn from the vertices give the same shape again, either rotated or mirrored. The centres of the arcs of the original shape are at the vertices of the new shape, and vice versa; the process is reversible.

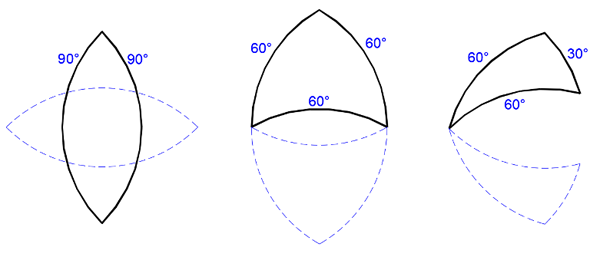
Three shapes with phantoms.

The second, new shape we can call the "phantom" of the first shape. So the phantom is the shape bounded by arcs drawn (with the same, original radius) from the original shape's vertices. It is the same shape, but transposed by rotation or reflection. The Reuleaux triangle above is self-referencing; it is its own phantom. You might of think these phantoms as floating invisibly along with the original shape: a sort of ghostly presence.

What we are interested in for the purpose of this article is a question mathematicians often ask themselves when confronted with a 2D shape: if you were given tiles in this shape, would you be able to tile the whole plane with those tiles; just like you can tile a plane with, say, squares?

For the four shapes we have looked at so far, the answer is "no". None of them can tile the plane alone (monohedrally). What you need for an arc-sided shape to tile the plane is an equal amount of concave (inward-bulging) and convex (outward-bulging) arc.

But let's look at a fifth shape – or rather, a family of shapes.

Tricurves

The lens is one of the simplest geometric shapes, consisting of two identical arcs joined at the ends. If we assume the radius of the arcs is 1 (for simplicity) then a lens can be described simply by the angle of the arcs.

We can pick a point on one of the arcs, dividing the arc into two parts, then make a lens from each part. If we subtract the two smaller lenses from the large lens we get a tricurve shape with unusual properties:

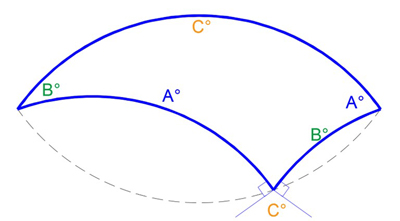
Tricurve geometry.

Any tricurve can tile the plane periodically: the pattern would look the same if you picked it up, moved it along in a certain direction and by a certain distance, and then put it down again, as shown below.

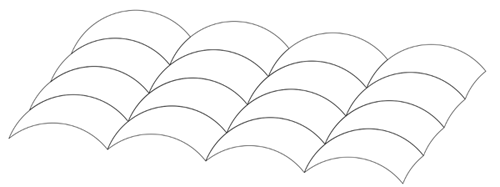
A periodic tiling.

If the angles of the arcs making up the tricurves are factors of 360° and the arcs are in pleasing proportions (such as 1:2:3), the tricurve is also gives surprising radial and non-periodic tilings. This makes for interesting puzzles that You can buy or make yourself:

Puzzles

Each tricurve is described by its three arc angles in ascending order, and the two concave arcs always add up to the large, convex arc. Puzzles made to date use tricurves with either 30°-60°-90° (top image above) or 36°-72°-180° arcs (bottom image above), but many agreeable angles and proportions can be used. In addition to monohedral tiling, tricurves can tile in sets of more than one size.

Phantoms of tricurves

What happens when we look at the phantoms of tricurves? We find that each tricurve has a phantom, which comes from a 180° rotation where the centre of rotation is unique to that shape. Depending on the tricurve, the phantom may overlap or may be quite separated from the original.

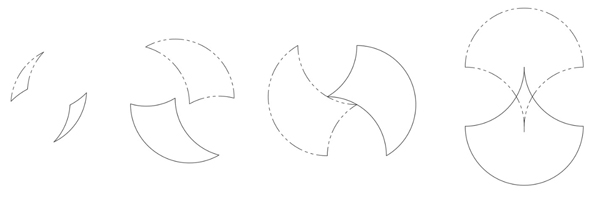
Some tricurves with phantoms.

To determine or visualise the position of the phantom for any tricurve, simply rotate the tricurve one-half turn and position the middle vertex (the one that connects the two concave sides) at the centre of the large arc of the original tricurve. For example, for any tricurve with large arc of 180°, the middle vertex of the phantom will be at the centre of that half circle regardless of the two smaller arcs:

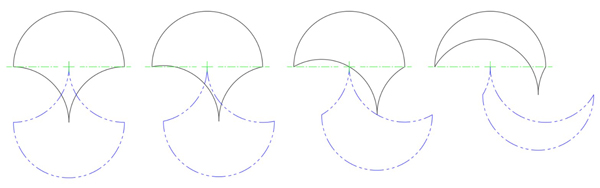
Some tricurves with 180° large arc.

For a symmetrical tricurve, the phantom is of the original tricurve revolved by 180°. But it is also a mirror image along the axis of symmetry of the original tricurve.

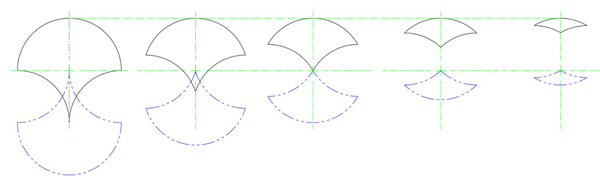
Some symmetrical tricurves and phantoms.

Tiling with phantoms

When we tile tricurves, and then look at the phantoms, we find to our delight that the phantoms also tile. Periodic tiling makes the phantoms tile periodically, as might be expected:

A periodic tiling with phantoms.

However this simple statement and image are a bit misleading: things are not as simple as they seem. In the above image you need to look closely to see which phantom goes with which original. When you do this you will see that in addition to the whole group of original tricurves rotating by 180°, the phantoms have switched positions. If we rotate the phantom group back 180°, we find the group has changed from the original group.

This is shown more clearly when we use tricurves of different sizes. In the example below the phantoms have not only rotated 180° but are on opposite sides of each other. They are no longer share the same arc:

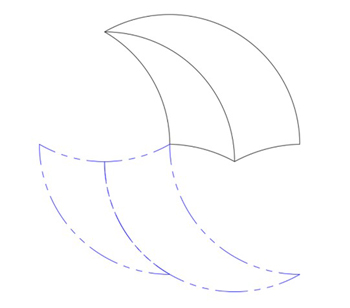
Transposed phantoms.

This kind of eerie behaviour also shows up in radial tiling. For the tricurve star or flower pattern below, the phantoms form a ring:

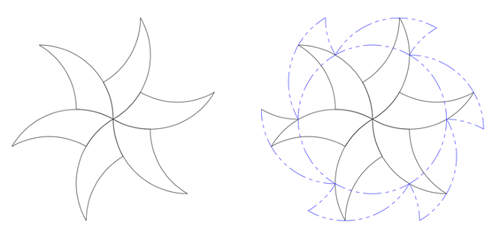
Flower pattern with phantom ring.

So when using tricurves to tile — from two pieces to tiling the whole plane — the phantoms will always also tile but in a non-intuitive, transposed manner. It is a bit spooky to think that as you fit together wooden tricurve pieces, the phantoms are also fitting together behind the scenes in an odd manner.

There is also another interesting question. What happens when you use tricurves to fill a specific shape? That's what we will find out on the next page.

Further reading

• Tiling with one arc-sided shape by Tim Lexen on mathblog
• Bending the law of sines by Tim Lexen on Aperiodical
• Combining tricurves by Tim Lexen on Aperiodical.
• Phantom tilings, by Tim Lexen on Aperiodical

About the author

Tim Lexen

Tim Lexen has been a mechanical engineer for 40+ years in various areas of new product R&D. He enjoys elegant solutions, the design process, tinkering, great communication, great stories, and family. He is married with 6 children and 10 grandchildren, and lives in the small town of Cumberland, Wisconsin, USA.