Graph theory knits a torus
If you've never heard of cubic Hamiltonian graphs before then take a look at Christopher Manning's wonderful cubic Hamiltonian graph builder. No, really, do! We too had never heard of them and now we think they are the bee's knees!
But what is a cubic Hamiltonian graph, you ask? A graph, of course, is just a bunch of points (vertices) connected by lines (edges). A cubic graph is a graph where every vertex has 3 edges – that is, each vertex is connected to exactly three others in the graph. And a Hamiltonian graph is a graph which has a closed loop of edges (a cycle) that visits each vertex in the graph once and only once, (this is called a Hamiltonian cycle). So a cubic Hamiltonian graph is a graph where each vertex is joined to exactly three others and the graph has a cycle visiting each vertex exactly once.
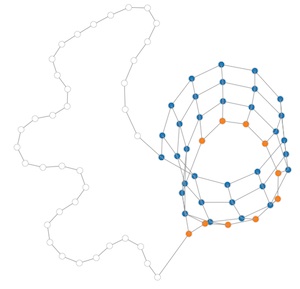
What has made us so excited about cubic Hamiltonian graphs is watching Manning's cubic Hamiltonian graph builder in action. The builder starts from the Hamiltonian cycle in the graph. This loop of edges accounts for two out of the three edges for every vertex in the graph. The builder then starts adding in the third edge for each vertex, knitting the graph together before your eyes. The creation of a torus is particularly beautiful to watch.
Manning uses something called the LCF notation to build the graphs. This ingenious notation succinctly describes the structure of cubic Hamiltonian graphs by describing how you add the extra edge to each vertex by counting backwards or forwards around the Hamiltonian cycle. For example our torus has the LCF notation [10]150. This means that every vertex is joined to another 10 edges along the cycle, and this process is repeated 150 times, once for each vertex, to complete the graph. (The 1st vertex is joined to the 11th, the 2nd to the 12th, the 3rd to the 13th, and so on...)
A graph represented by the LCF notation [10,7,4,-4,-7,10,-4,7,-7,4]2 starts with a cycle of 20 vertices – inside the square brackets is a list of instructions for 10 edges, and these are repeated twice, giving the total number of extra edges, and therefore vertices, as 20. In this graph the 1st vertex is joined to the 11th (a distance of 10 edges), the 2nd to the 9th (a distance of 7), the 3rd to the 7th (a distance of 4), the 4th to the 20th (a distance of -4, or counting backwards 4 edges), the 5th to the 18th (distance of -7), and so on. This graph is knitted into a dodecahedron.
Watching Manning's program knit together these graphs is beautiful to watch. But this mathematics has many important uses as well. Not only are Hamiltonian cycles important mathematically, they also have many useful applications. You can read more about graphs on Plus, and about the role Hamiltonian cycles play in bell ringing and DNA analysis. And you can read more about Christopher Manning's work on his blog.