How high is your frustum?

Rachel Thomas and Marianne Freiberger
Submitted by Rachel on June 26, 2015

Sometimes working on the maths describing something very concrete – something you can picture in your head – can lead you to stumble upon maths that you might not ever have imagined.

Let's go back the first century AD, when the Greek mathematician Heron was contemplating a frustum – a square based pyramid with the top lopped off. If the length of the sides of the square base is a, the length of the sides of the square top is b, and the length of the sloping edges running from top to bottom is c, how high is your frustum?

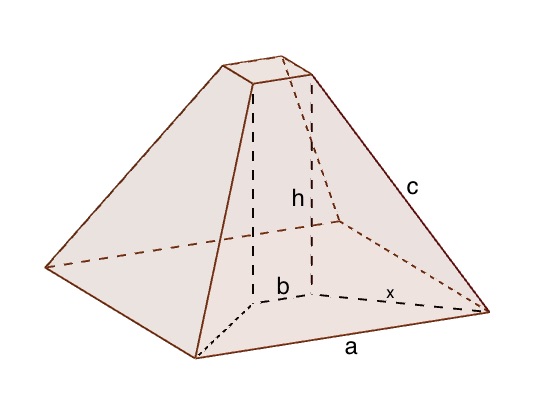
frustum

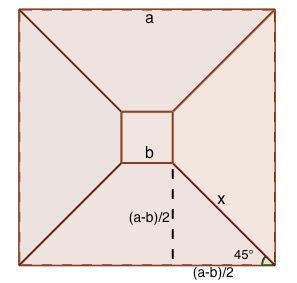
base of frustum

In the picture above the lengths of the sides and height are labelled as we've described. To the right is the view from the top of the frustum. In this view the square top is projected onto the square base, making a trapezoid with base length $a$, top length $b$, and side length $x$. The base of the trapezoid is $a-b$ longer than the top. Consider the right-angled triangle on each side of the trapezoid, formed by the its height, half the extra base length, $(a-b)/2$, and the side of length $x$. The angle to the base of the trapezoid is 45 degrees (as it is half of a right angle), and so the angles, and sides, either side of the right angle in this triangle are equal. This means the height of the trapezoid is also $(a-b)/2$. And so using Pythagoras' theorem we get

  \[ x=\sqrt{2 \left( \frac{(a-b)}{2} \right) ^2}=\frac{(a-b)}{\sqrt2}. \]    
We can now work out the height of our frustum using the right-angled triangle in the first picture, with height $h$, base $x$ and hypotenuse $c$. Using Pythagoras' theorem again we get:
  \[ h = \sqrt{c^2 - \frac{(a-b)^2}{2}}. \]    

Heron published this formula for the height of a frustum in his book Stereometria and demonstrated it with the values $a=10$, $b=2$ and $c=9$. The picture above is of a frustum with these measurements, and agrees with the formula that the height would be $7$.

He went on to try his formula with a different example, with values of $a=28$, $b=4$ and $c=15$. Plugging these values into the formula gives the height of such a frustum to be

  \[ h= \sqrt{225 - 288} = \sqrt{-63}. \]    
You won't be surprised that we can't draw you a picture of this frustum – it's a geometric impossibility!

Heron had come up with an impossible example. And he'd also given us the first recorded example of a calculation involving the square root of a negative number – the first step on our journey to discovering imaginary and complex numbers. But it was centuries before anyone would even contemplate such strange mathematical beasts, and so Heron fudged his working and recorded the answer as $\sqrt63$. One mathematical step at a time!

Rachel Thomas and Marianne Freiberger are the editors of Plus. They came across this story while researching their book Numericon: A journey through the hidden lives of numbers.

Comments

Submitted by Anonymous on June 26, 2015

It seems pretty obvious though for anyone contemplating the problem however briefly that "c" can be as large as one wishes, but it cannot be smaller than the minimum needed to connect the inner and outer squares (for the case they're in the same plane / height is zero). Not being able to handle the negative root is understandable but one would have expected Heron to realize there are "off limits" cases for his formula...

Submitted by Anonymous on June 29, 2015

Heron's tricky result can be reproduced on considering the familiar 2D right angled triangle. If h is the height, c the hypotenuse and a the base, then we know by Pythagoras that h = sqrt((c^2) - (a^2)). So if c is 5 and a is 4, then h is sqrt(25 - 16), which is 3. So far, so familiar.

But what if c is still 5, but a is longer, say 7? Then h is sqrt(25 - 49) = the square root of -14.

What would ancient geometers have made of that? Possibly much the same as the other commentator (see box below), namely that:

while c can be as long as one wishes, it cannot be smaller than the minimum needed to connect the other two sides of the triangle (for the case they're the same line, the height is zero).

If the base is longer than the hypotenuse then the latter can never connect up with the side which is perpendicular to the base, ie the height. Not only does such a "hypotenuse" no longer deserve that term, but more fundamentally it could have been considered in violation of Euclid's first two axioms:

1) To draw a straight line from any point to any point
2) To produce [extend] a finite straight line continuously in a straight line
(as worded in Wikipedia).

If c isn't long enough at present, then we've just got to extend it till it is, even if it means changing the given side ratios. Maybe a result incorporating the square root of 14 or of 63 (even if without a minus sign) would have been interpreted as some kind of clue to how much correction the error called for.

Chris G

Submitted by Anonymous on June 30, 2015

There I was, talking about error, and I go and make one of my own. 25 - 49 is 24, not 14.

This doesn't affect my arguments. One is that if we treat as an error a geometric specification in which c isn't long enough to connect up with another side, whether in the frustum or my example of a right angled triangle, then this suggests we could use the numerical result we do get as a means of correcting that specification, perhaps by simple addition of root 24 or 63.

Although I also suggested that such an original spec was in violation of Euclid's first two axioms, it isn't necessarily a "geometric inpossibility" (to quote the article) in the sense of being inconceivable or impossible to draw a picture of. Granted, in a 2D figure we can easily draw a line which stops short of another. In 3D this is at first consideration a bit more problematic, since a frustum or pyramid or whatever made out of say stone or clay has edges, instead of lines inked or scored into a supporting matrix like paper or sand. And how can you have such an edge which stops short and leaves a gap of empty space? Perhaps if the thing was made out of wire, or even better out of a big mass of paper mache with very thin straight tunnels in it corresponding to lines, in which ink has dried and set. If one of those tunnels didn't go all the way to another, then that could be our "impossible" frustum.

Chris G

Submitted by Dhanush on January 29, 2020

why do we take the angle to be 45 degrees.

Submitted by AlexT on September 14, 2020

x is the projection of c, and in a right pyramid (i.e. symmetric, with a regular polygon base), the projections of its edges on the base plane are also bisectors of the base's angles.